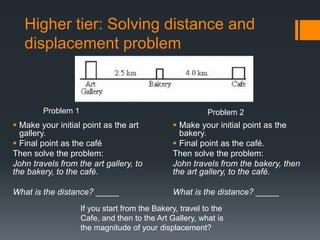
The document outlines key concepts in motion physics for grade 9, focusing on physical quantities, scalar and vector quantities, and the distinctions between distance and displacement. It explains the definitions of speed and velocity and includes problem-solving exercises to calculate them. Additionally, it provides typical speed values for various activities and modes of transport.

1. Motion
Physics – Grade 9

2. What are we going to learn?
 Define physical quantities
 Distinguish between scalar and vector quantities
 What is distance?
 What is displacement?
 Distinguish between distance and displacement
 Solve problems involving distance and displacement

3. Physical Quantities
What is physical quantity?
 Any quantity/quantities which can be measured
Types of physical quantity?
 Scalar physical quantity (Scalar quantity)
 Vector physical quantity (Vector quantity)

4. Scalar and Vector
What is scalar?
 A physical quantity which needs no specific direction
What is vector?
 A physical quantity which needs a specific direction

5. Types of scalar and vector
Scalar
 Length (16 cm)
 Temperature (102 degrees Celsius)
 Time (7 seconds)
 Mass
 Energy – the ability to do work

6. Types of scalar and vector
Vector
 Force (3N upwards)
 Weight
 Displacement (200 Miles NW)
 Acceleration (30 m2 upwards)
 Friction
 Velocity

7. What is distance?
 Distance is the measurement of how far objects are.
 In physics, distance is a physical length.
 It can be measured.
 It is a scalar.

8. Scalar and Vector
 Scalar quantities are measured with numbers or units. No
direction needed.
 Vector quantities are measured with numbers and units, but
also have a specific direction.
 If an arrowhead is on top, it is a vector quantity.
(example:
𝑉
)
 Scalar requires only magnitude part.
 Vector requires magnitude and direction.

9. What is displacement?
 Displacement is the initial position to the final position.
 In physics, it is a physical length.
 It is a physical quantity.
 It is a vector.

10. Distinguish: Distance and
Displacement

11. Explaining displacement through a
problem: Case 1
 Emily drives her car from San Francisco
to Sacramento. This is her journey.
The red line is her distance. (134 km)
The displacement is the direct
Line, with no zigzags or no left and right.
The displacement is the purple line.
The displacement is 100 km.
DISTANCE CANNOT BE 0, BUT
DISPLACEMENT CAN.

12.  Dave and Marty are swimmers. They
swim lengths of a 20 m pool.
Dave swims 3 lengths.
Marty swims 4 lengths.
a. Dave’s displacement is ________
b. Dave’s distance travelled is
________
c. Who has a greater displacement
Marty or Dave? ________
d. Who has a greater distance
travelled Marty or Dave? ______
Explaining displacement through a
problem: Case 2

13. Important notes to remember…
 If the person comes back, there is 0 displacement.
 For example, in the 2nd case. Marty and Dave swims the 1st
length, they have 20m distance travelled, and 20m
displacement. But, when they both swam the 2nd length, they
both have 40 distance travelled and 0 displacement.

14. Knowing the compass
Primary compass Secondary compass
In Grade 9, we make use of both compasses.

15. Higher tier: Solving distance and
displacement problem
 Make your initial point as the art
gallery.
 Final point as the café
Then solve the problem:
John travels from the art gallery, to
the bakery, to the café.
What is the distance? _____
 Make your initial point as the
bakery.
 Final point as the café.
Then solve the problem:
John travels from the bakery, then
the art gallery, to the café.
What is the distance? _____
Problem 1 Problem 2
If you start from the Bakery, travel to the
Cafe, and then to the Art Gallery, what is
the magnitude of your displacement?

16. Draw the diagram for the following
situations
1. David walks 3 km north, and then turns east
and walks 4 km.
2. Amy runs 200 meters south, then turns
around and runs 300 meters north.
3. Derrick crawls 40 meters south, and then
turns east and crawls 20 meters.
4. Ray runs 300 meters north, 100 meters west,
and then 300 meters south.
All diagrams should
be NOT TO SCALE

17. Before ending the lesson…
Displacement is lesser than distance.

18. Have we achieved the lesson
objective?
 Define physical quantities
 Distinguish between scalar and vector quantities
 What is distance?
 What is displacement?
 Distinguish between distance and displacement
 Solve problems involving distance and displacement

19. Have we achieved the lesson
objective?
Define physical quantities
Distinguish between scalar and vector quantities
What is distance?
What is displacement?
Distinguish between distance and displacement
Solve problems involving distance and displacement

20. What are we going to learn?
 What is speed?
 What is velocity?
 Distinguish between speed and velocity
 Know the standard units (SI units) for speed/velocity
 Know the non standard units for speed/velocity
 To calculate speed, distance, time using the triangle.
 To know that speed/velocity are similar in formulae, but vary
in characteristics.
 To solve speed-related problems.

21. What is speed? What is velocity?
 Speed is how fast an object travels.
 Velocity is speed in a particular direction.
 Speed is scalar.
 Velocity is vector.
 Velocity and Speed are same in graphs, but different in ways.

22. Distinguish: Speed and Velocity
 Speed is the rate of change of distance in the direction of
travel. Speedometers in cars measure speed. Directions
don’t matter.
 Velocity is the rate of change of displacement and has both
magnitude and direction.
32N downwards
Magnitude
Direction
Unit
Velocity

23. Why is Friction a vector quantity?
Friction is a force.
Force is a vector quantity.

24. Standard unit or Non Standard?
Length: SI unit = m (Meters)
Mass: SI unit = kg (Kilograms)
Time: SI unit = s (Seconds)
Length: Non standard unit = mm (milimeters), km
(kilometers), miles, feet
Mass: Non standard unit = mg (milligram), g
(gram)
Time: Non standard unit = minutes, hours

25. Calculating speed, distance, time
using the triangle
If you want to calculate
distance, cover the D.
If you want to calculate time,
cover the T.
If you want to calculate speed,
cover the S.

26. Calculating velocity, displacement
and time using the triangle
Exercise 1:
Using the triangle, calculate
formula for:
a) Velocity: ________
b) Distance: ________
c) Time: _______

27. Speed related problems
The Runners Association (TRA) wants to know how fast runners
ran. The runners’ goal is to run a 400m field. The runners
participating are:
- Jessy
- Robert
- Michel
Jessy ran in 5 seconds.
Robert ran in 12 seconds.
Michel in 6.17 seconds.
Calculate the speed of Jessy, Robert, Michel.
Who ran the fastest? _____________

28. Speed related problems
Ellie & Jenny sets a tortoise competition, to see who will
crawl the furthest.
Ellie’s tortoise crawled 0.10 m/s in 12 seconds.
Jenny’s tortoise crawled 0.08 m/s in 17 seconds.
Bill’s tortoise crawled 1 m/s in 30 seconds.
Natalie’s tortoise crawled 0.01 m/s in 6 seconds.
How far did?
a. Ellie’s tortoise crawl: _________
b. Jenny’s tortoise crawl: ________
c. Bill’s tortoise crawl: ________
d. Natalie’s tortoise crawl: _______
Which tortoise was the fastest? _____________

29. Speed related problems
Clark wants to go to the nearest hospital, to have a
recent checkup.
Clark searches the Internet for the nearest hospital.
They say that the nearest hospital is the Red Cross
Hospital, which is 12 km away.
He travels the hospital in 24 minutes, due to traffic.
a) Give the speed in which Clark travelled in m/s
________________. (meters per second)

30. Speed related problems
A Japanese bullet train can travel 80 m/s in 5 seconds.
a) Calculate the speed
b) People uses the bullet train to get to different places in
Japan:
Niga – 12 kilometers
Osaka – 30 kilometers
Honshu – 24.5 kilometers
Rita wants to go to Niga, how much time will it take?
Nelson wants to go to Osaka, how much time will it take?
Tim wants to go to Honshu, how much time will it take?

31. Have we achieved the learning
objective?
 What is speed?
 What is velocity?
 Distinguish between speed and velocity
 Know the standard units (SI units) for speed/velocity
 Know the non standard units for speed/velocity
 To calculate speed, distance, time using the triangle.
 To know that speed/velocity are similar in formulae, but vary
in characteristics.
 To solve speed-related problems.

32. Have we achieved the learning
objective?
What is speed?
What is velocity?
Distinguish between speed and velocity
Know the standard units (SI units) for speed/velocity
Know the non standard units for speed/velocity
To calculate speed, distance, time using the triangle.
To know that speed/velocity are similar in formulae, but vary
in characteristics.
To solve speed-related problems.

33. What are we going to learn?
 Typical speeds

34. Typical speeds
 Cycling – 10 m/s
 Running – 12 m/s
 Walking – 1.4 m/s
 Wind – 4 m/s
 Train – 50 km/h – Convert the speed to m/s
 Car – 60 km/h – Convert the speed to m/s
 Sound – 340 m/s
 Jet – 250 m/s
 Light – 3 x 108 m/s
Bullet – 340 m/s

35. Typical speeds
 Cycling – 10 m/s
 Running – 12 m/s
 Walking – 1.4 m/s
 Wind – 4 m/s
 Train – 13.89 m/s – Did you get it right?
 Car – 16.67 m/s – Did you get it right?
 Sound – 340 m/s
 Jet – 250 m/s
 Light – 3 x 108 m/s
Bullet – 340 m/s