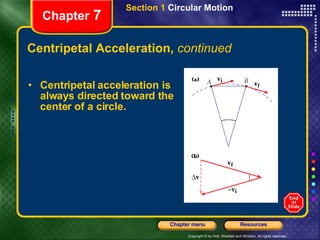
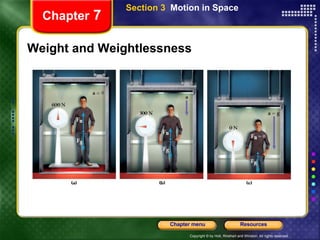
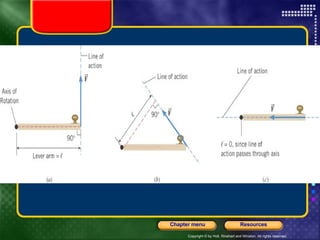
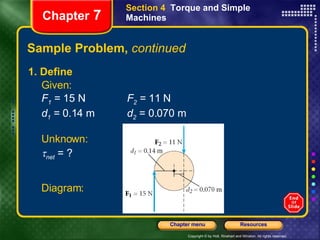
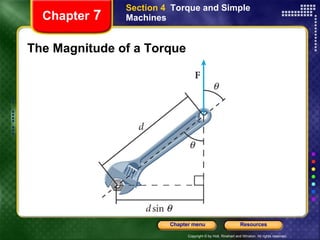
This document provides an overview of key concepts from a physics chapter on circular motion, gravity, and simple machines. It includes objectives, definitions, equations, examples, and sample problems for key topics like centripetal acceleration and force, Newton's law of universal gravitation, orbital motion, torque, and simple machines. It also provides multiple choice questions for standardized test preparation.

1. Chapter Presentation Transparencies Sample Problems Visual Concepts Standardized Test Prep Resources

2. Table of Contents Section 1 Circular Motion Section 2 Newton’s Law of Universal Gravitation Section 3 Motion in Space Section 4 Torque and Simple Machines Circular Motion and Gravitation Chapter 7

3. Objectives Solve problems involving centripetal acceleration. Solve problems involving centripetal force. Explain how the apparent existence of an outward force in circular motion can be explained as inertia resisting the centripetal force. Chapter 7 Section 1 Circular Motion

4. Centripetal Acceleration Chapter 7 Section 1 Circular Motion

5. Centripetal Acceleration The acceleration of an object moving in a circular path and at constant speed is due to a change in direction. An acceleration of this nature is called a centripetal acceleration. Chapter 7 Section 1 Circular Motion

6. Centripetal Acceleration, continued Centripetal acceleration is always directed toward the center of a circle. Chapter 7 Section 1 Circular Motion

7. Centripetal Force Consider a ball of mass m that is being whirled in a horizontal circular path of radius r with constant speed. Chapter 7 The force exerted by the string has horizontal and vertical components. The vertical component is equal and opposite to the gravitational force . Thus, the horizontal component is the net force. This net force, which is is directed toward the center of the circle, is a centripetal force. Section 1 Circular Motion

8. Centripetal Force, continued Newton’s second law can be combined with the equation for centripetal acceleration to derive an equation for centripetal force: Chapter 7 Section 1 Circular Motion

9. Centripetal Force, continued Chapter 7 Centripetal force is simply the name given to the net force on an object in uniform circular motion . Section 1 Circular Motion

10. Centripetal Force, continued Chapter 7 If the centripetal force vanishes, the object stops moving in a circular path. Section 1 Circular Motion

11. Describing a Rotating System Chapter 7 To better understand the motion of a rotating system, consider a car traveling at high speed and approaching an exit ramp that curves to the left. As the driver makes the sharp left turn, the passenger slides to the right and hits the door. What causes the passenger to move toward the door? Section 1 Circular Motion

12. Describing a Rotating System, continued Chapter 7 Section 1 Circular Motion As the car enters the ramp and travels along a curved path, the passenger, because of inertia, tends to move along the original straight path. If a sufficiently large centripetal force acts on the passenger, the person will move along the same curved path that the car does. The origin of the centripetal force is the force of friction between the passenger and the car seat. If this frictional force is not sufficient, the passenger slides across the seat as the car turns underneath.

13. Objectives Explain how Newton’s law of universal gravitation accounts for various phenomena, including satellite and planetary orbits, falling objects, and the tides. Apply Newton’s law of universal gravitation to solve problems. Section 2 Newton’s Law of Universal Gravitation Chapter 7

14. Gravitational Force, continued The centripetal force that holds the planets in orbit is the same force that pulls an apple toward the ground— gravitational force. Gravitational force is the mutual force of attraction between particles of matter. Gravitational force depends on the masses and on the distance between them . Chapter 7 Section 2 Newton’s Law of Universal Gravitation

15. Gravitational Force, continued Chapter 7 Section 2 Newton’s Law of Universal Gravitation The constant G , called the constant of universal gravitation , equals 6.673  10 –11 N•m 2 /kg.

16. Newton’s Law of Universal Gravitation Chapter 7 Section 2 Newton’s Law of Universal Gravitation

17. Applying the Law of Gravitation Newton’s law of gravitation accounts for ocean tides. High and low tides are partly due to the gravitational force exerted on Earth by its moon. The tides result from the difference between the gravitational force at Earth’s surface and at Earth’s center. Chapter 7 Section 2 Newton’s Law of Universal Gravitation

18. Weight and Weightlessness Chapter 7 Section 3 Motion in Space

19. Objectives Distinguish between torque and force. Calculate the magnitude of a torque on an object. Identify the six types of simple machines. Calculate the mechanical advantage of a simple machine. Section 4 Torque and Simple Machines Chapter 7

20. The Magnitude of a Torque Torque is a quantity that measures the ability of a force to rotate an object around some axis. The perpendicular distance from the axis of rotation to a line drawn along the direction of the force is equal to d sin  and is called the lever arm.  = Fd sin  torque = force  lever arm Section 4 Torque and Simple Machines Chapter 7

21. The Magnitude of a Torque, continued The applied force may act at an angle. However, the direction of the lever arm ( d sin  ) is always perpendicular to the direction of the applied force, as shown here. Section 4 Torque and Simple Machines Chapter 7

23. Torque Chapter 7 Section 4 Torque and Simple Machines

24. The Sign of a Torque The torque is positive if the rotation is counterclockwise and negative if the rotation is clockwise. Section 4 Torque and Simple Machines Chapter 7

25. The Sign of a Torque Chapter 7 Section 4 Torque and Simple Machines

26. Sample Problem Torque A basketball is being pushed by two players during tip-off. One player exerts an upward force of 15 N at a perpendicular distance of 14 cm from the axis of rotation.The second player applies a downward force of 11 N at a distance of 7.0 cm from the axis of rotation. Find the net torque acting on the ball about its center of mass. Chapter 7 Section 4 Torque and Simple Machines

27. Sample Problem, continued 1. Define Given: F 1 = 15 N F 2 = 11 N d 1 = 0.14 m d 2 = 0.070 m Chapter 7 Section 4 Torque and Simple Machines Diagram: Unknown:  net = ?

28. Sample Problem, continued 2. Plan Choose an equation or situation: Apply the definition of torque to each force,and add up the individual torques. Chapter 7 Section 4 Torque and Simple Machines Tip: The factor sin  is not included in the torque equation because each given distance is the perpendicular distance from the axis of rotation to a line drawn along the direction of the force. In other words, each given distance is the lever arm.  = Fd  net =  1 +  2 = F 1 d 1 + F 2 d 2

29. Sample Problem, continued 4. Evaluate The net torque is negative,so the ball rotates in a clockwise direction. Chapter 7 Section 4 Torque and Simple Machines Calculate Substitute the values into the equation and solve: First,determine the torque produced by each force.Use the standard convention for signs.   1 = F 1 d 1 = (15 N)(0.14 m) = 2.1 N•m  2 = F 2 d 2 = (–11 N)(0.070 m) = –0.77 N•m  net =  1 +  2 = 2.1 N•m – 0.77 N•m  net = 1.33 N•m

30. Simple Machines All machines are combinations or modifications of six fundamental types of machines, called simple machines. These six simple machines are the lever, pulley, inclined plane, wheel and axle, wedge, and screw. Section 4 Torque and Simple Machines Chapter 7

31. Simple Machines Chapter 7 Section 4 Torque and Simple Machines

32. Simple Machines, continued Section 4 Torque and Simple Machines Chapter 7 The diagrams show two examples of a trunk being loaded onto a truck. In the first example, a force ( F 1 ) of 360 N moves the trunk through a distance ( d 1 ) of 1.0 m. This requires 360 N•m of work. In the second example, a lesser force ( F 2 ) of only 120 N would be needed (ignoring friction), but the trunk must be pushed a greater distance ( d 2 ) of 3.0 m. This also requires 360 N•m of work.

33. Simple Machines, continued The simple machines we have considered so far are ideal, frictionless machines. Real machines, however, are not frictionless. Some of the input energy is dissipated as sound or heat. The efficiency of a machine is the ratio of useful work output to work input. Section 4 Torque and Simple Machines Chapter 7 The efficiency of an ideal (frictionless) machine is 1, or 100 percent. The efficiency of real machines is always less than 1.

34. Mechanical Efficiency Chapter 7 Section 4 Torque and Simple Machines

35. Multiple Choice 1. An object moves in a circle at a constant speed. Which of the following is not true of the object? A. Its acceleration is constant. B. Its tangential speed is constant. C. Its velocity is constant. D. A centripetal force acts on the object. Standardized Test Prep Chapter 7

36. Multiple Choice 1. An object moves in a circle at a constant speed. Which of the following is not true of the object? A. Its acceleration is constant. B. Its tangential speed is constant. C. Its velocity is constant. D. A centripetal force acts on the object. Standardized Test Prep Chapter 7

37. Multiple Choice, continued Use the passage below to answer questions 2–3. A car traveling at 15 m/s on a flat surface turns in a circle with a radius of 25 m. 2. What is the centripetal acceleration of the car? F. 2.4  10 -2 m/s 2 G. 0.60 m/s 2 H. 9.0 m/s 2 J. zero Standardized Test Prep Chapter 7

38. Multiple Choice, continued Use the passage below to answer questions 2–3. A car traveling at 15 m/s on a flat surface turns in a circle with a radius of 25 m. 2. What is the centripetal acceleration of the car? F. 2.4  10 -2 m/s 2 G. 0.60 m/s 2 H. 9.0 m/s 2 J. zero Standardized Test Prep Chapter 7

39. Multiple Choice, continued Use the passage below to answer questions 2–3. A car traveling at 15 m/s on a flat surface turns in a circle with a radius of 25 m. 3. What is the most direct cause of the car’s centripetal acceleration? A. the torque on the steering wheel B. the torque on the tires of the car C. the force of friction between the tires and the road D . the normal force between the tires and the road Standardized Test Prep Chapter 7

40. Multiple Choice, continued Use the passage below to answer questions 2–3. A car traveling at 15 m/s on a flat surface turns in a circle with a radius of 25 m. 3. What is the most direct cause of the car’s centripetal acceleration? A. the torque on the steering wheel B. the torque on the tires of the car C. the force of friction between the tires and the road D . the normal force between the tires and the road Standardized Test Prep Chapter 7

41. Multiple Choice, continued 4. Earth ( m = 5.97  10 24 kg) orbits the sun ( m = 1.99  10 30 kg) at a mean distance of 1.50  10 11 m. What is the gravitational force of the sun on Earth? ( G = 6.673  10 -11 N•m 2 /kg 2 ) F. 5.29  10 32 N G. 3.52  10 22 N H. 5.90  10 –2 N J. 1.77  10 –8 N Standardized Test Prep Chapter 7

42. Multiple Choice, continued 4. Earth ( m = 5.97  10 24 kg) orbits the sun ( m = 1.99  10 30 kg) at a mean distance of 1.50  10 11 m. What is the gravitational force of the sun on Earth? ( G = 6.673  10 -11 N•m 2 /kg 2 ) F. 5.29  10 32 N G. 3.52  10 22 N H. 5.90  10 –2 N J. 1.77  10 –8 N Standardized Test Prep Chapter 7

43. Multiple Choice, continued 5. Which of the following is a correct interpretation of the expression ? A. Gravitational field strength changes with an object’s distance from Earth. B. Free-fall acceleration changes with an object’s distance from Earth. C. Free-fall acceleration is independent of the falling object’s mass. D. All of the above are correct interpretations. Standardized Test Prep Chapter 7

44. Multiple Choice, continued 5. Which of the following is a correct interpretation of the expression ? A. Gravitational field strength changes with an object’s distance from Earth. B. Free-fall acceleration changes with an object’s distance from Earth. C. Free-fall acceleration is independent of the falling object’s mass. D. All of the above are correct interpretations. Standardized Test Prep Chapter 7

45. Multiple Choice, continued 6. What data do you need to calculate the orbital speed of a satellite? F. mass of satellite, mass of planet, radius of orbit G. mass of satellite, radius of planet, area of orbit H. mass of satellite and radius of orbit only J. mass of planet and radius of orbit only Standardized Test Prep Chapter 7

46. Multiple Choice, continued 6. What data do you need to calculate the orbital speed of a satellite? F. mass of satellite, mass of planet, radius of orbit G. mass of satellite, radius of planet, area of orbit H. mass of satellite and radius of orbit only J. mass of planet and radius of orbit only Standardized Test Prep Chapter 7

47. Multiple Choice, continued 7. Which of the following choices correctly describes the orbital relationship between Earth and the sun? A. The sun orbits Earth in a perfect circle. B. Earth orbits the sun in a perfect circle. C. The sun orbits Earth in an ellipse, with Earth at one focus. D. Earth orbits the sun in an ellipse, with the sun at one focus. Standardized Test Prep Chapter 7

48. Multiple Choice, continued 7. Which of the following choices correctly describes the orbital relationship between Earth and the sun? A. The sun orbits Earth in a perfect circle. B. Earth orbits the sun in a perfect circle. C. The sun orbits Earth in an ellipse, with Earth at one focus. D. Earth orbits the sun in an ellipse, with the sun at one focus. Standardized Test Prep Chapter 7

49. Multiple Choice, continued Use the diagram to answer questions 8–9. Standardized Test Prep Chapter 7 8. The three forces acting on the wheel have equal magnitudes. Which force will produce the greatest torque on the wheel? F. F 1 G. F 2 H. F 3 J. Each force will produce the same torque.

50. Multiple Choice, continued Use the diagram to answer questions 8–9. Standardized Test Prep Chapter 7 8. The three forces acting on the wheel have equal magnitudes. Which force will produce the greatest torque on the wheel? F. F 1 G. F 2 H. F 3 J. Each force will produce the same torque.

51. Multiple Choice, continued Use the diagram to answer questions 8–9. Standardized Test Prep Chapter 7 9. If each force is 6.0 N, the angle between F 1 and F 2 is 60.0°, and the radius of the wheel is 1.0 m, what is the resultant torque on the wheel? A. –18 N•m C. 9.0 N•m B. –9.0 N•m D. 18 N•m

52. Multiple Choice, continued Use the diagram to answer questions 8–9. Standardized Test Prep Chapter 7 9. If each force is 6.0 N, the angle between F 1 and F 2 is 60.0°, and the radius of the wheel is 1.0 m, what is the resultant torque on the wheel? A. –18 N•m C. 9.0 N•m B. –9.0 N•m D. 18 N•m

53. Multiple Choice, continued 10. A force of 75 N is applied to a lever. This force lifts a load weighing 225 N. What is the mechanical advantage of the lever? F. 1/3 G. 3 H. 150 J. 300 Standardized Test Prep Chapter 7

54. Multiple Choice, continued 10. A force of 75 N is applied to a lever. This force lifts a load weighing 225 N. What is the mechanical advantage of the lever? F. 1/3 G. 3 H. 150 J. 300 Standardized Test Prep Chapter 7

55. Multiple Choice, continued 11. A pulley system has an efficiency of 87.5 percent. How much work must you do to lift a desk weighing 1320 N to a height of 1.50 m? A. 1510 J B. 1730 J C. 1980 J D. 2260 J Standardized Test Prep Chapter 7

56. Multiple Choice, continued 11. A pulley system has an efficiency of 87.5 percent. How much work must you do to lift a desk weighing 1320 N to a height of 1.50 m? A. 1510 J B. 1730 J C. 1980 J D. 2260 J Standardized Test Prep Chapter 7

57. Multiple Choice, continued 12. Which of the following statements is correct? F. Mass and weight both vary with location. G. Mass varies with location, but weight does not. H. Weight varies with location, but mass does not. J. Neither mass nor weight varies with location. Standardized Test Prep Chapter 7

58. Multiple Choice, continued 12. Which of the following statements is correct? F. Mass and weight both vary with location. G. Mass varies with location, but weight does not. H. Weight varies with location, but mass does not. J. Neither mass nor weight varies with location. Standardized Test Prep Chapter 7

59. Multiple Choice, continued 13. Which astronomer discovered that planets travel in elliptical rather than circular orbits? A. Johannes Kepler B. Nicolaus Copernicus C. Tycho Brahe D. Claudius Ptolemy Standardized Test Prep Chapter 7

60. Multiple Choice, continued 13. Which astronomer discovered that planets travel in elliptical rather than circular orbits? A. Johannes Kepler B. Nicolaus Copernicus C. Tycho Brahe D. Claudius Ptolemy Standardized Test Prep Chapter 7

61. Short Response 14. Explain how it is possible for all the water to remain in a pail that is whirled in a vertical path, as shown below. Standardized Test Prep Chapter 7

62. Short Response 14. Explain how it is possible for all the water to remain in a pail that is whirled in a vertical path, as shown below. Standardized Test Prep Chapter 7 Answer: The water remains in the pail even when the pail is upside down because the water tends to move in a straight path due to inertia.

63. Short Response, continued 15. Explain why approximately two high tides take place every day at a given location on Earth. Standardized Test Prep Chapter 7

64. Short Response, continued 15. Explain why approximately two high tides take place every day at a given location on Earth. Answer: The moon’s tidal forces create two bulges on Earth. As Earth rotates on its axis once per day, any given point on Earth passes through both bulges. Standardized Test Prep Chapter 7

65. Short Response, continued 16. If you used a machine to increase the output force, what factor would have to be sacrificed? Give an example. Standardized Test Prep Chapter 7

66. Short Response, continued 16. If you used a machine to increase the output force, what factor would have to be sacrificed? Give an example. Answer: You would have to apply the input force over a greater distance. Examples may include any machines that increase output force at the expense of input distance. Standardized Test Prep Chapter 7

67. Extended Response 17. Mars orbits the sun ( m = 1.99  10 30 kg) at a mean distance of 2.28  10 11 m. Calculate the length of the Martian year in Earth days. Show all of your work. ( G = 6.673  10 –11 N•m 2 /kg 2 ) Standardized Test Prep Chapter 7

68. Extended Response 17. Mars orbits the sun ( m = 1.99  10 30 kg) at a mean distance of 2.28  10 11 m. Calculate the length of the Martian year in Earth days. Show all of your work. ( G = 6.673  10 –11 N•m 2 /kg 2 ) Standardized Test Prep Chapter 7 Answer: 687 days

69. Centripetal Acceleration Chapter 7 Section 1 Circular Motion

70. Centripetal Force Chapter 7 Section 1 Circular Motion

71. Kepler’s Laws Chapter 7 Section 3 Motion in Space

72. The Magnitude of a Torque Section 4 Torque and Simple Machines Chapter 7

73. Simple Machines Section 4 Torque and Simple Machines Chapter 7