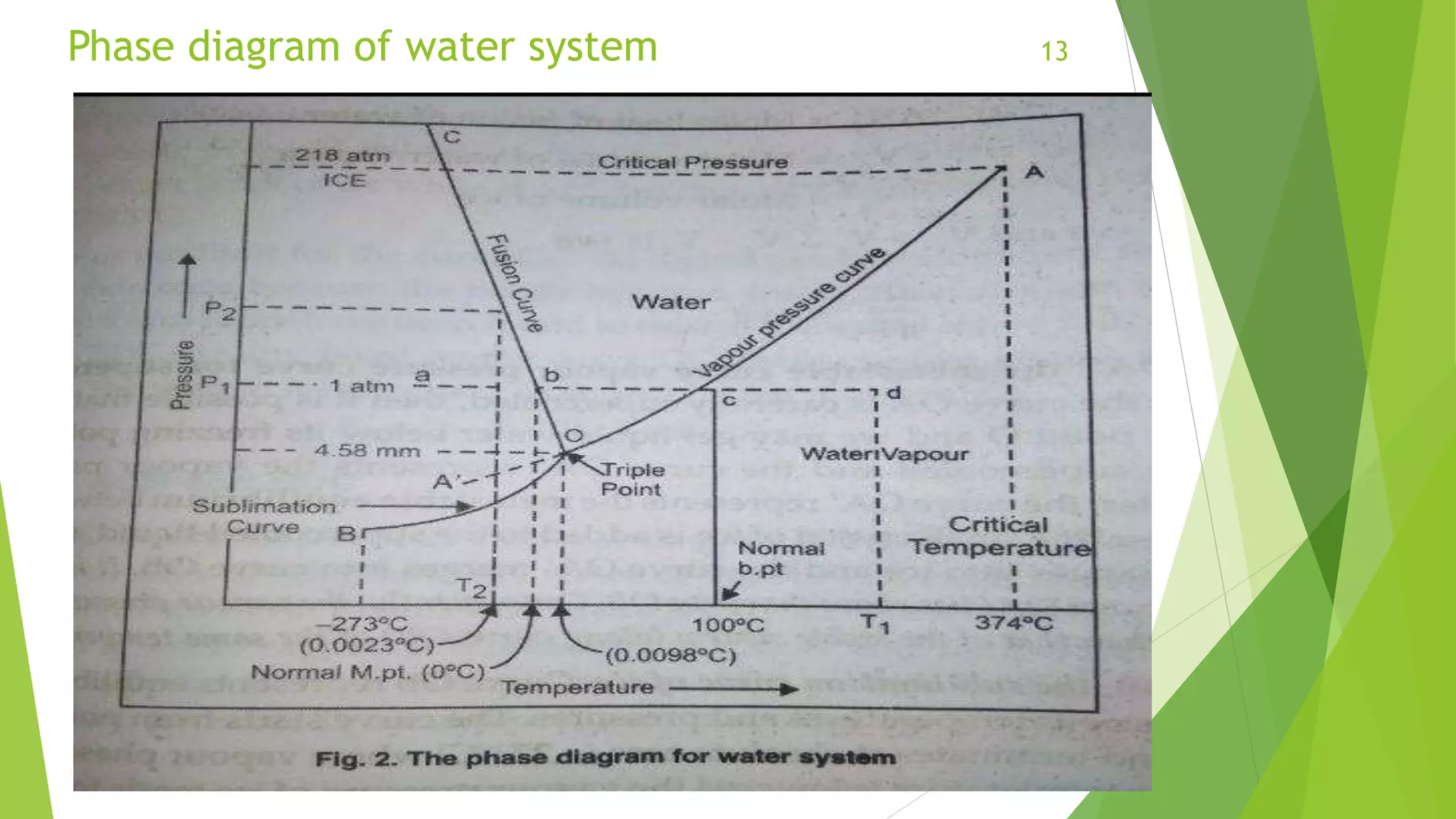
The document provides an overview of phase equilibria, including definitions of phases, components, and degrees of freedom, along with equilibrium types and the conditions necessary for phase equilibrium. It explains Gibbs' phase rule, which mathematically relates the number of phases, components, and degrees of freedom in a system. Additionally, the document discusses the phase diagram of water, illustrating the relationships and conditions under which different phases coexist.

1. Phase Equilibria 1
Presented by:
Meenakshi khatkar
M.Sc. Previous year
180000701029

2. Content 2
 Introduction
 Definition of phase ,component and degree of
freedom
 Equilibrium and it’s type
 Conditions for phase equilibrium
 Gibbs phase rule
 One component system
 Conculsion
 References

3. Introduction 3
Phase equilibrium is the study of the equilibrium between two or more phases of
heterogeneous systems.
The number of phases that can exist together at equilibrium depends upon the
temperature,pressure,and composition of various phases
J.W.Gibbs gave a generalization which applicable to all heterogeneous equilibria known as
phase rule.
It is mathematically defined as:
F = C-P+2
Where F = number of degrees of freedom
C = number of components
P = number of phases

4. Phase 4
Phase is defined as any homogeneous and physically distinct part of a system
which is separated by a well defined boundary, physically and chemically
different from other parts of system.
A system may contain one or more than one
phases. For example a system containing ice,
Liquid water and water vapour is a three
Phase system

5. Component 5
For a system in equilibrium it is the minimum number of independent chemical
constituents in terms of which the composition of each phase can be expressed
either directly or in terms of a chemical equation.
The independent chemical constituents is the one whose concentration can be
varied independent of other constituent of the system.
For example : NaCl solution it contain solid NaCl and water.There are two
component NaCl and water. The composition of each phase can be expressed in
terms of two constituent NaCl and water.
Note:
The number of components may or may not be equal to the actual
number of constituents present in the system

6. Degree of freedom 6
Degree of freedom is defined as the number of variables,
such as temperature, pressure and concentration, which
can be varied independently without changing the
number of phases.
The degree of freedom in phase rule equations is given by
F = C-P+2
For example a system containing two component gaseous
mixture have three degree of freedom.
Same result is obtained by phase rule equation
F = C-P+2 = 2-1+2 = 3

7. Equilibrium 7
A system is said to be in the state of equilibrium if the properties like
temperature, pressure and composition etc. of the various phases do
not under go any change with time.
Equilibrium is of two types:
1. True equilibrium : A system is said to be in a state of true
equilibrium if the same state can be obtained by approach from
either direction.For example, the following equilibrium
This equilibrium can be attained from either side i.e. By melting
of ice or by freezing of water. Hence,it is a true equilibrium.

8. 2 Metastable equilibrium: 8
A system is said to be in a state of metastable equilibrium
if the same state can be approached only from one direction and that too by very careful
change of conditions.
For example, water at -2°C can be obtained by careful cooling of
water without appearance of ice but it is not possible to obtain it by melting of ice.Hence,
water at -2°C is said be in a state of metastable equilibrium.
In this figure curve OA` represents the metastable equilibrium between liquid water and
vapour phase.
If a small crystal of ice is added to the supercooled
liquid , the liquid at once solidifies and changes into
Ice and curve OA` merges into curve OB.

9. Condition for phase equilibrium 9
A system having more than one phase is in equilibrium if following conditions are
satisfied.
1. Thermal Equilibrium: In this state the temperature of all the phases must be
same. If temperature is not same than heat will flow from one part of system
to another part.
2. Mechanical Equilibrium: In this condition ,all the phases of system are under
the same pressure . Otherwise , the volume change from one phase to
another phase.
3. Chemical Equilibrium: In the state of chemical equilibrium, the chemical
potential of a component must be same in all phases.

10. Gibbs Phase Rule 10
J. Willard Gibbs gives a relationship between the number of phases,P, the
number of components,C, and the number of degree of freedom F . This
relationship is known as phase rule.
F=C-P+2
Derivation of phase rule
Consider a heterogeneous system having P phases (P1,P2,P3,....Pn) and
components C (C1,C2,C3,….Cn). Then degree of freedom F is given by
F = (Total no. Of variables)- ( No. Of relationship between variables at
equilibrium)

11. Cont... 11
The total number of of variables
1. one is temperature and one is pressure variable for whole system.
2. P(C-1) are composition variables.
Total number of variables = P(C-1) +1+1
= P(C-1)+2
. Number of relationship between variables at equilibrium
C(P-1)
Thus degree of freedom = [P(C-1)+2]-[C(P-1)] = PC-P+2-PC+C = C-P+2
This Is the Gibbs phase rule.

12. One component system 12
Under nomal conditions water exists in phases namely liquid water,
ice and water vapour.
All these phases can be represented by single constituent ‘Water’
so it is one component system.
The number phases that can exists at any time depends on
the conditions of temperature and pressure.

13. Phase diagram of water system 13

14. 14
Phase diagram of water consists the following three curves
1 Curve OA:It gives the equilibrium between liquid water and water vapours .it is
called vapour pressure curve of water. The degree of freedom for this curve is given by:
F =C-P+2 =1-2+2 = 1
2 Curve OB: It is the curve which represents the equilibrium between the ice and water
vapours. This is sublimation curve of ice. The degree of freedom for this curve is given by:
F= C-P+2 =1-2+2 =1
3 Curve OC: It is the curve which represents the equilibrium between ice and liquid water.
This is the melting point curve of ice.Degree of freedom for this curve is given by:
F = C-P+2 =1-2+2 = 1
4 Curve OA’ : This is the metastable curve for supercooled liquid. It is seen in the phase
diagram curve OA’ lies above the curve OB. Hence ,vapour pressure of metastable system is
higher than of the stable system at same temperature.

15. Areas AOC,AOB and BOC 15
The areas AOC, AOB and BOC in the phase diagram show the conditions of temperature and pressure at
which a single phase ice,water or vapours can exist.
It is necessary to specify both temperature and pressure to define a system in these areas. The degree
of freedom for these areas is given by:
F =C-P+2 = 1-1+2 = 2
So these areas are bivariant system.
Triple point:
The point ‘O’ in the phase diagram represents triple point of water system
The curve oA ,OB and OC meets at triple point ‘O’ . At this point all the three phases
are exist in equilibrium . Only one such point is possible.
The degree of freedom at this point is given by:
F =C-P+2 = 1-3+2 = 0
So the system is invariant or non-variant at this point.

16. Conclusion: 16
Phase equilibria gives the conditions that must be specified for a system to exist
in equilibrium.
A generalization is given by J.W.Gibbs which predict the conditions that a must
specified for a system to exhibit equilibrium.
This generalization is known as phase rule. This rule is mathematically given as:
F= C-P+2
The degree of freedom is calculated by this rule.

17. References 17
1. ^ Gibbs,J.W., Scientific Papers (Daver , New York,1961)
2. ^Atkins ,P.W. ; de Paula, J.(2006) Physical chemistry (8th
ed.). Oxford University
3. Principles of physical chemistry by B.R.Puri ,L.R.Sharm,
Madan S.Pathania.
4. Physical chemistry by S.Kiran.

18. Thankyou