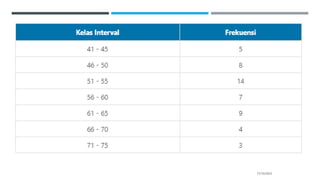
Teks tersebut membahas tentang tabel distribusi frekuensi yang merupakan tabel yang mengelompokkan dan menghitung frekuensi dari data. Tabel ini terdiri dari dua kolom yaitu kelas dan frekuensi, digunakan untuk meringkas data besar menjadi lebih mudah dipahami. Teks tersebut juga menjelaskan langkah-langkah pembuatan tabel distribusi frekuensi mulai dari menentukan rentang nilai, jumlah kelas, panjang kelas, h

1. MENCARI MEAN

2. PENDAHULUAN
 Dari setiap kumpulan data, terdapat tiga ukuran atau tiga nilai
statistik yang dapat mewakili data tersebut, yaitu rataan (mean),
median, dan modus. Ketiga nilai tersebut dikenal sebagai ukuran
pemusatan data atau ukuran tendensi sentral, karena memiliki nilai
yang cenderung sama.
17/10/2023

3. PEMUSATAN DATA

7.  Solusi : (cara 1) Cara Langsung
 Solusi : (cara 2) dugaan sementara / coding

8. TABEL DISTIBUSI FREKUENSI
 Tabel distribusi frekuensi sering sekali digunakan sebagai cara untuk bisa meringkas data
yang digunakan dalam penelitian atau berbagai kebutuhan lainnya. Data yang jumlahnya
banyak akan bisa lebih mudah dimengerti apabila diubah menjadi bentuk tabel ini. Sehingga
data akan bisa lebih terorganisir dengan baik.
 Tabel distribusi frekuensi adalah sebuah tabel atau bagan yang akan merangkum nilai dan
frekuensi dari sebuah data. Ini adalah cara yang berguna untuk mengatur data jika kamu
memiliki daftar angka yang mewakili frekuensi hasil tertentu dalam sampel. Tabel distribusi
frekuensi memiliki dua kolom. Kolom pertama mencantumkan berbagai hasil yang terjadi
dalam data, dan kolom kedua mencantumkan frekuensi dari hasil. Frekuensi akan bisa
memberitahukan seberapa sering sesuatu nilai terjadi.
17/10/2023

9. ADA BAGIAN-BAGIAN YANG AKAN DIPAKAI DALAM MEMBUAT SEBUAH
TABEL DISTRIBUSI FREKUENSI.
1. Kelas-kelas
Kelompok nilai data atau variabel dari suatu data
acak.
2. Batas kelas
Nilai-nilai yang membatasi kelas yang satu dengan
kelas yang lain. Batas kelas menjadi batas semu
dari setiap kelas, karena di antara kelas yang satu
dengan kelas yang lain masih terdapat tempat
untuk angka-angka tertentu. Terdapat dua batas
kelas untuk data-data yang telah diurutkan, yaitu:
batas kelas bawah (lower class limits) dan batas
kelas atas (upper class limits).
3. Tepi kelas
Merupakan batas nyata kelas, yaitu batas kelas
yang tidak memiliki tempat untuk angka tertentu
antara kelas yang satu dengan kelas yang lain. Hal
ini juga dibagi menjadi tepi bawah kelas dan tepi
atas kelas. 17/10/2023
4. Titik tengah kelas atau tanda kelas
Merupakan angka atau nilai data yang tepat terletak di
tengah dari suatu kelas. Titik tengah kelas menjadi nilai
yang akan merepresentasikan nilai dalam data. Titik
tengah kelas akan bisa diketahui melalui rumus ini:
½ (batas atas + batas bawah) kelas
5. Interval kelas
Bagian yang memisahkan kelas yang satu dengan kelas
yang lain.
6. Panjang interval kelas atau luas kelas
Jarak antara tepi atas kelas dan tepi bawah kelas.
7. Frekuensi kelas
Seberapa banyaknya data yang termasuk ke dalam kelas
tertentu dari data acak.

10. Tabel distribusi frekuensi
 Tentukan nilai rentang
 Tentukan banyak kelas yang digunakan
ATURAN STURGES dengan rumusnya sebagai berikut :
 Tentukan panjang kelas

11. SOAL LATIHAN BERSAMA YAK
17/10/2023
Diketahui nilai statistika kelas 3 PAI sbg berikut:
Tentukan mean dengan solusi 1 dan ke 2
23 60 79 32 57 74 52 70 82 36
80 77 81 95 41 65 92 85 55 76
52 10 64 75 78 25 80 98 81 67
41 71 83 54 64 72 88 62 74 43
60 78 89 76 84 48 84 90 15 79
34 67 17 82 69 74 63 80 85 61

12.  Hitung jarak atau rentangan (R).
Rumus: R = data tertinggi – data terkecil. = 98 – 10 =88
 Menghitung jumlah kelas.
K = 1 + 3,3 log n
K = 1 + 3,3 log 60
K = 1 + 3,3 (1.778151)
K = 1 + 5,8678
K = 6,86 (dibulatkan 7)
17/10/2023
 Hitung panjang kelas (P).
P = R/K
P = 88/7 = 12,57 (dibulatkan 13)

13. Kelas Interval Frekuensi
10-22 3
23-35 4
36-48 5
49-61 8
62-73 11
74-86 23
87-99 6

14. SOLUSI 1
Kelas Interval Frekuensi xi Fixi
10-22 3 16 48
23-35 4 29 116
36-48 5 42 210
49-61 8 55 440
62-73 11 68 748
74-86 23 81 1863
87-99 6 94 564
Jumlah 60 3989
17/10/2023
3989
60
66,48

15. SOLUSI 2
Kelas Interval Frekuensi xi Ci Fi Ci
10-22 3 16 -3 -9
23-35 4 29 -2 -8
36-48 5 42 -1 -5
49-61 8 55 0 0
62-73 11 68 1 11
74-86 23 81 2 46
87-99 6 94 3 18
Jumlah 60 53
17/10/2023
55 + 13
53
60
55 + 13 0,883
55 + 11,483
66,483

16. CONTOH SOAL
Terdapat data nilai
ujian kelas 10 adalah
sebagai berikut.
Buatlah distribusi
frekuensi dari data di
atas.
17/10/2023
75 52 67 55 53 58 59 58 43 45
55 48 50 65 48 52 54 56 65 58
55 53 55 61 63 70 71 49 51 62
52 49 50 51 63 66 67 71 44 60
48 50 43 43 60 51 63 64 65 54

17. STEP BY STEP
 setelah itu hitung jarak atau rentangan (R).
Rumus: R = data tertinggi – data terkecil.
 Menghitung jumlah kelas.
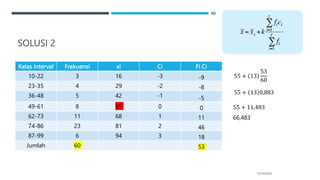
K = 1 + 3,3 log n
K = 1 + 3,3 log 50
K = 1 + 3,3 (1.69897)
K = 1 + 5,60
K = 6,60 (dibulatkan 7)
17/10/2023
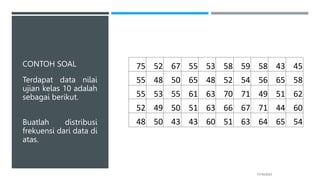
[nilai tertinggi – nilai terendah] = 75 – 43 = 32
 Hitung panjang kelas (P).
P = R/K
P = 32/7 = 4,57 (dibulatkan 5)

18. 17/10/2023

19. LATIHAN
 Buat tabel distribusi frekuensi
23 60 79 32 57 74 52 70 82 36
80 77 81 95 41 65 92 85 55 76
52 10 64 75 78 25 80 98 81 67
41 71 83 54 64 72 88 62 74 43
60 78 89 76 84 48 84 90 15 79
34 67 17 82 69 74 63 80 85 61
17/10/2023