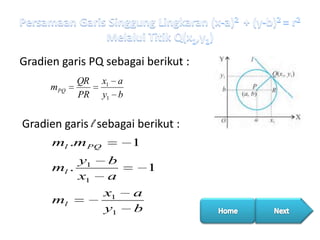
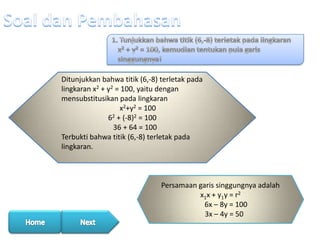
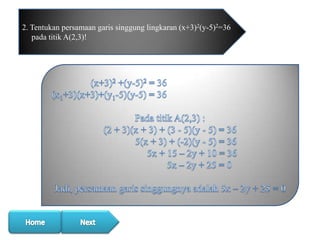
Dokumen tersebut membahas tentang penentuan persamaan garis singgung lingkaran melalui suatu titik. Metode yang digunakan adalah dengan menyamakan persamaan garis singgung dengan persamaan lingkaran pada titik tersebut. Persamaan garis singgung diperoleh dengan menggunakan rumus umum persamaan garis singgung lingkaran. Contoh soal penentuan persamaan garis singgung lingkaran melalui beberapa titik diberikan.

5. Maka, persamaan garis singgungnya sebagai berikut :
y
y
y1
mg ( x
x1 )
y1
x1
(x
y1
x1 )
y1 ( y
OP tegak lurus garis g, maka :
mOP .m g
y1
.m g
x1
mg
1
1
x1
y1
y1 )
x1 ( x
y1 y
2
y1
x1 x
y1 y
2
x1
x1 x
y1 y
r2
x1 x
2
x1
2
y1
x1 )

6. Gradien garis PQ sebagai berikut :
mPQ
QR
PR
x1 a
y1 b
Gradien garis l sebagai berikut :
ml .mPQ
y1
ml .
x1
ml
1
b
a
x1
y1
1
a
b

7. Jadi, pers.garis l dengan gradien ml dan melalui titik Q adalah :
y
y
(y
yy1
yy1
by by1
by
y1
y1
y1 )( y1
b)
( x1
a )( x
by1
x1 x
x12
y12
x1 x ax ax1
ml ( x
x1 )
x1 a
(x
y1 b
x12
x1 )
x1 )
ax ax1
y12 ......( )
1
Untuk Q terletak pada lingkaran, maka :
(x - a) 2
(x1 - a) 2
x12
2ax1
a2
r2
2ax1
y12
2by1
( y b) 2
r2
( y1
b) 2
r2
2by1
b2
r2
a2
b2
x12
y12 .....(2)

8. Dari persamaan (1) dan (2), diperoleh :
yy1 by by1
x1 x ax ax1
x12
y12
yy1 by by1
x1 x ax ax1
r2
2ax1
a2
r2
yy1 by by1
b2
x1 x ax ax1
a)
a)(x a) ( y1 b)( y b)
b2
r2
Jadi, persamaan garis singgung lingkaran (x - a) 2
yang melalui titik pada lingkaran adalah
( x1
a2
r2
( y b)( y1 b) ( x a)( x1
( x1
2by1
a)(x a) ( y1
b)( y b)
r2
(y - b) 2
r2

9. Dari pers.garis singgung melalui titik Q pada lingkaran (x - a) 2
( x1
x1 x ax1
x1 x a ( x1
x1 x
y1 y a ( x1
a )(x a ) ( y1
ax a 2
x) a 2
x) b( y1
r2
r2
b)( y b)
y1 y by1
by b 2
r2
y1 y b( y1
y) b 2
r2
b2
0
y) a 2
Misalkan A
x1 x
( y b) 2
-a, B
r2
-b, dan C
y1 y a ( x1
x) b( y1
x1 x
A( x1
y1 y
a2
y) a 2
x) B ( y1
b2
b2
r 2 , maka :
r2
0
y) C
0

10. Tentukan pers. garis singgung yang melalui titik A(2,1) pada lingkaran
x 2 + y 2 - 2x + 4y – 5 = 0
A(2,1)  x1 = 2, y1 = 1
x2 + y2 -2x +4y -5 = 0  A = -1, B = 2, C = -5
Persamaan garis singgung melalui titik A(2,1) :
x1x + y1y +Ax1 + Ax + By1 + By + C = 0
2x + 1y + (-1)2 + (-1)x + 2.1 + 2y-5 = 0
2x + y - 2 – x + 2 + 2y – 5 = 0
x + 3y – 5 = 0

11. Ditunjukkan bahwa titik (6,-8) terletak pada
lingkaran x2 + y2 = 100, yaitu dengan
mensubstitusikan pada lingkaran
x2+y2 = 100
62 + (-8)2 = 100
36 + 64 = 100
Terbukti bahwa titik (6,-8) terletak pada
lingkaran.
Persamaan garis singgungnya adalah
x1x + y1y = r2
6x – 8y = 100
3x – 4y = 50

12. 2. Tentukan persamaan garis singgung lingkaran (x+3)2(y-5)2=36
pada titik A(2,3)!

13. 3. Tentukan pers. garis singgung yang melalui titik
A(3,4) pada lingkaran x 2 + y 2 - 4x + 2y – 21 = 0
A(2,1)  x1 = 3, y1 = 4
x2 + y2 - 4x + 2y - 21 = 0  A = -2, B = 1, C = -21
Persamaan garis singgung melalui titik A(2,1) :
x1x + y1y +Ax1 + Ax + By1 + By + C = 0
3x + 4y + (-2)2 + (-2)x + 1.4 + 1y - 21 = 0
3x + 4y - 4 – 2x + 4 + y – 21 = 0
x + 5y – 21 = 0