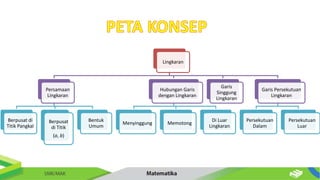
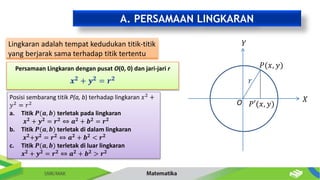
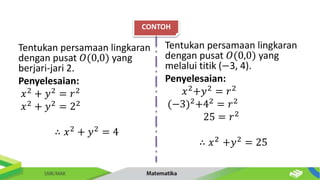
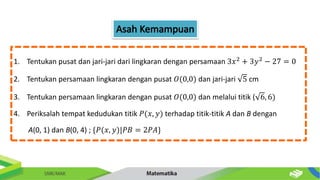
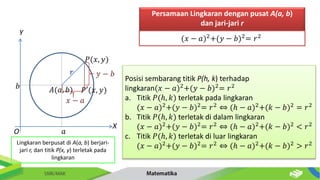
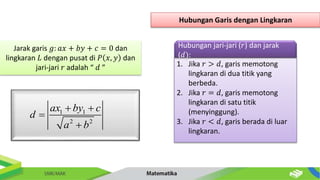
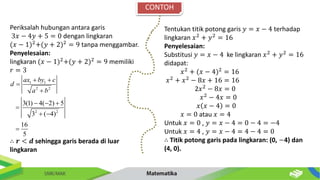
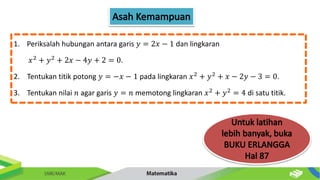
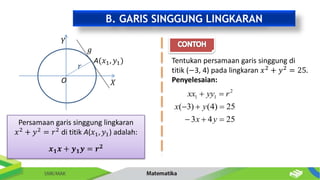
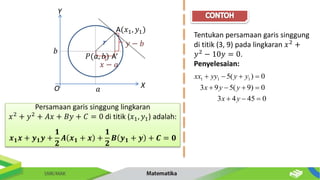
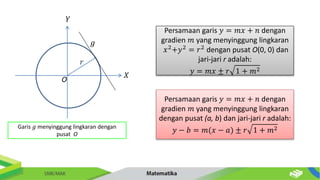
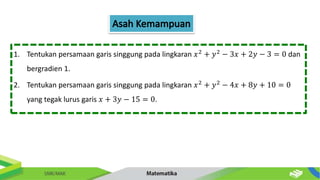
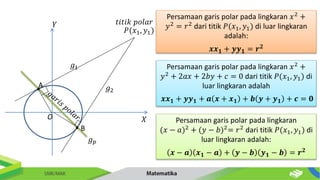
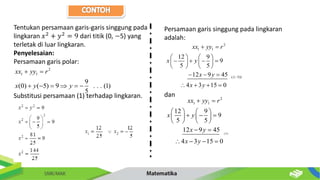
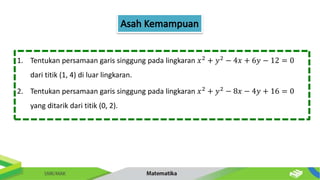
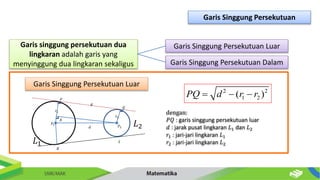
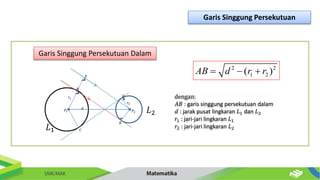
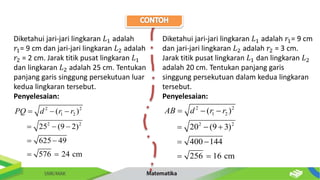
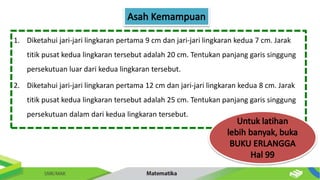
Dokumen ini membahas tentang persamaan lingkaran dan hubungannya dengan titik-titik serta garis. Diberikan metode untuk menentukan posisi titik terhadap lingkaran serta cara mencari persamaan garis singgung dan hubungan antara dua lingkaran. Contoh-contoh soal disertakan untuk memperjelas penerapan konsep tersebut.

1. Matematika
MEDIA MENGAJAR
UNTUK SMK/MAK KELAS XI

2. BAB 3
Persamaan Lingkaran
Sumber: flickr.com/©Ron
Cogswell

3. Lingkaran
Persamaan
Lingkaran
Berpusat di
Titik Pangkal
Berpusat
di Titik
(a, b)
Bentuk
Umum
Hubungan Garis
dengan Lingkaran
Menyinggung Memotong
Di Luar
Lingkaran
Garis
Singgung
Lingkaran
Garis Persekutuan
Lingkaran
Persekutuan
Dalam
Persekutuan
Luar

4. A. PERSAMAAN LINGKARAN
Lingkaran adalah tempat kedudukan titik-titik
yang berjarak sama terhadap titik tertentu
𝑟
O 𝑃′(𝑥, 𝑦)
𝑃(𝑥, 𝑦)
𝑋
𝑌
Persamaan Lingkaran dengan pusat O(0, 0) dan jari-jari r
𝒙𝟐 + 𝒚𝟐 = 𝒓𝟐
Posisi sembarang titik P(a, b) terhadap lingkaran 𝑥2
+
𝑦2
= 𝑟2
a. Titik 𝑷(𝒂, 𝒃) terletak pada lingkaran
𝒙𝟐
+ 𝒚𝟐
= 𝒓𝟐
⇔ 𝒂𝟐
+ 𝒃𝟐
= 𝒓𝟐
b. Titik 𝑷(𝒂, 𝒃) terletak di dalam lingkaran
𝒙𝟐
+𝒚𝟐
= 𝒓𝟐
⇔ 𝒂𝟐
+ 𝒃𝟐
< 𝒓𝟐
c. Titik 𝑷(𝒂, 𝒃) terletak di luar lingkaran
𝒙𝟐
+ 𝒚𝟐
= 𝒓𝟐
⇔ 𝒂𝟐
+ 𝒃𝟐
> 𝒓𝟐

5. CONTOH
Tentukan persamaan lingkaran
dengan pusat 𝑂(0,0) yang
berjari-jari 2.
Penyelesaian:
𝑥2 + 𝑦2 = 𝑟2
𝑥2 + 𝑦2 = 22
∴ 𝑥2
+ 𝑦2
= 4
Tentukan persamaan lingkaran
dengan pusat 𝑂(0,0) yang
melalui titik (−3, 4).
Penyelesaian:
𝑥2
+𝑦2
= 𝑟2
(−3)2+42 = 𝑟2
25 = 𝑟2
∴ 𝑥2 +𝑦2 = 25

6. 1. Tentukan pusat dan jari-jari dari lingkaran dengan persamaan 3𝑥2
+ 3𝑦2
− 27 = 0
2. Tentukan persamaan lingkaran dengan pusat 𝑂(0,0) dan jari-jari 5 cm
3. Tentukan persamaan lingkaran dengan pusat 𝑂(0,0) dan melalui titik ( 6, 6)
4. Periksalah tempat kedudukan titik 𝑃(𝑥, 𝑦) terhadap titik-titik A dan B dengan
A(0, 1) dan B(0, 4) ; {𝑃(𝑥, 𝑦)|𝑃𝐵 = 2𝑃𝐴}

7. 𝑟 𝑦 − 𝑏
𝑥 − 𝑎
𝐴(𝑎, 𝑏)
𝑃(𝑥, 𝑦)
𝑃′(𝑥, 𝑦)
𝑎
𝑏
X
Y
O
Persamaan Lingkaran dengan pusat A(a, b)
dan jari-jari r
Posisi sembarang titik P(h, k) terhadap
lingkaran(𝑥 − 𝑎)2+(𝑦 − 𝑏)2= 𝑟2
a. Titik 𝑃(ℎ, 𝑘) terletak pada lingkaran
(𝑥 − 𝑎)2
+(𝑦 − 𝑏)2
= 𝑟2
⇔ (ℎ − 𝑎)2
+(𝑘 − 𝑏)2
= 𝑟2
b. Titik 𝑃(ℎ, 𝑘) terletak di dalam lingkaran
(𝑥 − 𝑎)2
+(𝑦 − 𝑏)2
= 𝑟2
⇔ (ℎ − 𝑎)2
+(𝑘 − 𝑏)2
< 𝑟2
c. Titik 𝑃(ℎ, 𝑘) terletak di luar lingkaran
(𝑥 − 𝑎)2
+(𝑦 − 𝑏)2
= 𝑟2
⇔ (ℎ − 𝑎)2
+(𝑘 − 𝑏)2
> 𝑟2
(𝑥 − 𝑎)2
+(𝑦 − 𝑏)2
= 𝑟2
Lingkaran berpusat di A(a, b) berjari-
jari r, dan titik P(x, y) terletak pada
lingkaran

8. Bentuk Umum Persamaan Lingkaran dengan pusat A(a, b) dan jari-jari r
𝑥2 + 𝑦2 + 𝐴𝑥 + 𝐵𝑦 + 𝐶 = 0 ; 𝐴, 𝐵, 𝐶 bilangan real
dengan:
𝐴 = −2𝑎, 𝐵 = −2𝑏, dan 𝐶 = 𝑎2 + 𝑏2 − 𝑟2
memiliki pusat di 𝑃 −
𝐴
2
, −
𝐵
2
dan 𝑟 =
𝐴2
4
+
𝐵2
4
− 𝐶

9. Tentukan persamaan lingkaran
yang berpusat di P(−5, 6) dan
melalui titik A(3, −9).
Penyelesaian:
2 2
2 2 2
2 2 2
2 2
adalah jarak titik :
(3 ( 5)) ( 9 6) 17
Persamaan lingkarannya:
( ) ( )
( ( 5)) ( 6) 17
( 5) ( 6) 289
r AP
r
x a y b r
x y
x y
      
   
    
   
Tentukan pusat dan jari-jari lingkaran
𝑥2 + 𝑦2 + 6𝑥 − 8𝑦 − 24 = 0
Penyelesaian:
2 2
2 2
2 6 3
2 8 4
Titik Pusat ( 3, 4)
( 3) ( 4) ( 24)
49 7
a a
b b
r a b c
    
     
 
  
     
 

10. Hubungan Garis dengan Lingkaran
Substitusi antara garis 𝑔: 𝑦 = 𝑚𝑥 + 𝑛 dengan lingkaran 𝐿: 𝑥2
+ 𝑦2
+ 2𝑎𝑥 + 2𝑏𝑦 + 𝑐 = 0 menghasilkan:
2 2 2
(1 ) (2 2 2 ) 2 0
m x mn a bm x n bn c
       
Jika D < 0 , garis g tidak
memotong lingkaran L
𝒈
(a, b)
O
X
Y
Jika D > 0 , garis g
memotong lingkaran L di
dua titik yang berbeda.
𝒈
(a, b)
O
X
Y
Jika D = 0 , garis g
menyinggung lingkaran L di
satu titik.
𝑔
(a, b)
O
X
Y

11. Jarak garis 𝑔: 𝑎𝑥 + 𝑏𝑦 + 𝑐 = 0 dan
lingkaran 𝐿 dengan pusat di 𝑃 𝑥, 𝑦 dan
jari-jari 𝑟 adalah “ 𝑑 ”
1 1
2 2
ax by c
d
a b
 


1. Jika 𝑟 > 𝑑, garis memotong
lingkaran di dua titik yang
berbeda.
2. Jika 𝑟 = 𝑑, garis memotong
lingkaran di satu titik
(menyinggung).
3. Jika 𝑟 < 𝑑, garis berada di luar
lingkaran.
Hubungan jari-jari (𝑟) dan jarak
(𝑑):
Hubungan Garis dengan Lingkaran

12. CONTOH
Periksalah hubungan antara garis
3𝑥 − 4𝑦 + 5 = 0 dengan lingkaran
(𝑥 − 1)2
+(𝑦 + 2)2
= 9 tanpa menggambar.
Penyelesaian:
lingkaran (𝑥 − 1)2
+(𝑦 + 2)2
= 9 memiliki
𝑟 = 3
∴ 𝒓 < 𝒅 sehingga garis berada di luar
lingkaran
Tentukan titik potong garis 𝑦 = 𝑥 − 4 terhadap
lingkaran 𝑥2
+ 𝑦2
= 16
Penyelesaian:
Substitusi 𝑦 = 𝑥 − 4 ke lingkaran 𝑥2
+ 𝑦2
= 16
didapat:
𝑥2
+ (𝑥 − 4)2
= 16
𝑥2
+ 𝑥2
− 8𝑥 + 16 = 16
2𝑥2
− 8𝑥 = 0
𝑥2
− 4𝑥 = 0
𝑥 𝑥 − 4 = 0
𝑥 = 0 atau 𝑥 = 4
Untuk 𝑥 = 0 , 𝑦 = 𝑥 − 4 = 0 − 4 = −4
Untuk 𝑥 = 4 , 𝑦 = 𝑥 − 4 = 4 − 4 = 0
∴ Titik potong garis pada lingkaran: (0, −4) dan
(4, 0).
1 1
2 2
2 2
3(1) 4( 2) 5
3 ( 4)
16
5
ax by c
d
a b
 


  

 


13. 1. Periksalah hubungan antara garis 𝑦 = 2𝑥 − 1 dan lingkaran
𝑥2
+ 𝑦2
+ 2𝑥 − 4𝑦 + 2 = 0.
2. Tentukan titik potong 𝑦 = −𝑥 − 1 pada lingkaran 𝑥2
+ 𝑦2
+ 𝑥 − 2𝑦 − 3 = 0.
3. Tentukan nilai 𝑛 agar garis 𝑦 = 𝑛 memotong lingkaran 𝑥2
+ 𝑦2
= 4 di satu titik.

14. B. GARIS SINGGUNG LINGKARAN
Persamaan garis singgung lingkaran
𝑥2
+ 𝑦2
= 𝑟2
di titik A(𝑥1, 𝑦1) adalah:
𝒙𝟏𝒙 + 𝒚𝟏𝒚 = 𝒓𝟐
𝑟
O
A(𝑥1, 𝑦1)
𝑋
𝑌
𝑔
Tentukan persamaan garis singgung di
titik (−3, 4) pada lingkaran 𝑥2 + 𝑦2 = 25.
Penyelesaian:
2
1 1
( 3) (4) 25
3 4 25
xx yy r
x y
x y
 
  
  

15. Persamaan garis singgung lingkaran
𝑥2 + 𝑦2 + 𝐴𝑥 + 𝐵𝑦 + 𝐶 = 0 di titik (𝑥1, 𝑦1) adalah:
𝒙𝟏𝒙 + 𝒚𝟏𝒚 +
𝟏
𝟐
𝑨 𝒙𝟏 + 𝒙 +
𝟏
𝟐
𝑩 𝒚𝟏 + 𝒚 + 𝑪 = 𝟎
𝑟 𝑦 − 𝑏
𝑥 − 𝑎
𝑃(𝑎, 𝑏)
A(𝑥1, 𝑦1)
A’
𝑎
𝑏
X
Y
O
Tentukan persamaan garis singgung
di titik (3, 9) pada lingkaran 𝑥2 +
𝑦2
− 10𝑦 = 0.
Penyelesaian:
1 1 1
5( ) 0
3 9 5( 9) 0
3 4 45 0
xx yy y y
x y y
x y
   
   
  

16. Persamaan garis 𝑦 = 𝑚𝑥 + 𝑛 dengan
gradien 𝑚 yang menyinggung lingkaran
𝑥2+𝑦2 = 𝑟2 dengan pusat O(0, 0) dan
jari-jari r adalah:
𝑦 = 𝑚𝑥 ± 𝑟 1 + 𝑚2
𝑟
O
𝑋
𝑌
𝑔
Persamaan garis 𝑦 = 𝑚𝑥 + 𝑛 dengan
gradien 𝑚 yang menyinggung lingkaran
dengan pusat (a, b) dan jari-jari r adalah:
𝑦 − 𝑏 = 𝑚(𝑥 − 𝑎) ± 𝑟 1 + 𝑚2
Garis 𝑔 menyinggung lingkaran dengan
pusat O

17. Tentukan persamaan garis singgung
dengan gradien 2 pada lingkaran 𝑥2
+
𝑦2
= 16.
Penyelesaian:
2
1
2 4 1 4
2 4 5
2 4 5 dan 2 4 5
y mx r m
x
x
y x y x
  
  
 
    
Tentukan persamaan garis singgung
dengan gradien 2 pada lingkaran
(𝑥 − 1)2
+(𝑦 − 2)2
= 4.
Penyelesaian:
2
( ) 1
2 2( 1) 2 1 4
2 2 5
2 2 5 dan 2 2 5
y b m x a r m
y x
y x
y x y x
    
    
 
    

18. 1. Tentukan persamaan garis singgung pada lingkaran 𝑥2
+ 𝑦2
− 3𝑥 + 2𝑦 − 3 = 0 dan
bergradien 1.
2. Tentukan persamaan garis singgung pada lingkaran 𝑥2 + 𝑦2 − 4𝑥 + 8𝑦 + 10 = 0
yang tegak lurus garis 𝑥 + 3𝑦 − 15 = 0.

19. Persamaan garis polar pada lingkaran 𝑥2
+
𝑦2
= 𝑟2
dari titik 𝑃(𝑥1, 𝑦1) di luar lingkaran
adalah:
𝒙𝒙𝟏 + 𝒚𝒚𝟏 = 𝒓𝟐
O
A
𝑋
𝑌
𝑔𝑝
B
𝑔1
𝑔2
𝑃(𝑥1, 𝑦1)
𝑡𝑖𝑡𝑖𝑘 𝑝𝑜𝑙𝑎𝑟
Persamaan garis polar pada lingkaran 𝑥2 +
𝑦2
+ 2𝑎𝑥 + 2𝑏𝑦 + 𝑐 = 0 dari titik 𝑃(𝑥1, 𝑦1) di
luar lingkaran adalah
𝒙𝒙𝟏 + 𝒚𝒚𝟏 + 𝒂 𝒙 + 𝒙𝟏 + 𝒃 𝒚 + 𝒚𝟏 + 𝒄 = 𝟎
Persamaan garis polar pada lingkaran
(𝑥 − 𝑎)2
+ (𝑦 − 𝑏)2
= 𝑟2
dari titik 𝑃(𝑥1, 𝑦1) di
luar lingkaran adalah:
𝒙 − 𝒂 𝒙𝟏 − 𝒂 + 𝒚 − 𝒃 𝒚𝟏 − 𝒃 = 𝒓𝟐

20. Tentukan persamaan garis-garis singgung pada
lingkaran 𝑥2
+ 𝑦2
= 9 dari titik (0, −5) yang
terletak di luar lingkaran.
Penyelesaian:
Persamaan garis polar:
Substitusi persamaan (1) terhadap lingkaran.
2
1 1
9
(0) ( 5) 9 . . . (1)
5
xx yy r
x y y
 
     
Persamaan garis singgung pada lingkaran
adalah:
dan
2
1 1
(:( 3))
12 9
9
5 5
12 9 45
4 3 15 0
xx yy r
x y
x y
x y

 
   
   
   
   
  
   
(:3)
2
1 1
12 9
9
5 5
12 9 45
4 3 15 0
xx yy r
x y
x y
x y
 
   
  
   
   
 
   

21. 1. Tentukan persamaan garis singgung pada lingkaran 𝑥2 + 𝑦2 − 4𝑥 + 6𝑦 − 12 = 0
dari titik (1, 4) di luar lingkaran.
2. Tentukan persamaan garis singgung pada lingkaran 𝑥2
+ 𝑦2
− 8𝑥 − 4𝑦 + 16 = 0
yang ditarik dari titik (0, 2).

22. Garis Singgung Persekutuan Luar
Garis Singgung Persekutuan
Garis singgung persekutuan dua
lingkaran adalah garis yang
menyinggung dua lingkaran sekaligus
dengan:
𝑃𝑄 : garis singgung persekutuan luar
𝑑 : jarak pusat lingkaran 𝐿1 dan 𝐿2
𝑟1 : jari-jari lingkaran 𝐿1
𝑟2 : jari-jari lingkaran 𝐿2
2 2
1 2
( )
PQ d r r
  
𝐴
𝑃1
𝑃
𝑅
𝑟1
𝐿1
𝐿2
𝑔
𝑑
𝑆
𝑄
𝑃2
𝑟2
Garis Singgung Persekutuan Luar
Garis Singgung Persekutuan Dalam

23. Garis Singgung Persekutuan Dalam
dengan:
𝐴𝐵 : garis singgung persekutuan dalam
𝑑 : jarak pusat lingkaran 𝐿1 dan 𝐿2
𝑟1 : jari-jari lingkaran 𝐿1
𝑟2 : jari-jari lingkaran 𝐿2
2 2
1 2
( )
AB d r r
  
𝐸
𝑃1
A
𝐶
𝑟1
𝐿1
𝐿2
𝑑
𝐵
𝐷
𝑃2
𝑟2
Garis Singgung Persekutuan

24. 2 2
1 2
2 2
( )
25 (9 2)
625 49
576 24 cm
PQ d r r
  
  
 
 
Diketahui jari-jari lingkaran 𝐿1 adalah
𝑟1= 9 cm dan jari-jari lingkaran 𝐿2 adalah
𝑟2 = 2 cm. Jarak titik pusat lingkaran 𝐿1
dan lingkaran 𝐿2 adalah 25 cm. Tentukan
panjang garis singgung persekutuan luar
kedua lingkaran tersebut.
Penyelesaian:
Diketahui jari-jari lingkaran 𝐿1 adalah 𝑟1= 9 cm
dan jari-jari lingkaran 𝐿2 adalah 𝑟2 = 3 cm.
Jarak titik pusat lingkaran 𝐿1 dan lingkaran 𝐿2
adalah 20 cm. Tentukan panjang garis
singgung persekutuan dalam kedua lingkaran
tersebut.
Penyelesaian:
2 2
1 2
2 2
( )
20 (9 3)
400 144
256 16 cm
AB d r r
  
  
 
 

25. 1. Diketahui jari-jari lingkaran pertama 9 cm dan jari-jari lingkaran kedua 7 cm. Jarak
titik pusat kedua lingkaran tersebut adalah 20 cm. Tentukan panjang garis singgung
persekutuan luar dari kedua lingkaran tersebut.
2. Diketahui jari-jari lingkaran pertama 12 cm dan jari-jari lingkaran kedua 8 cm. Jarak
titik pusat kedua lingkaran tersebut adalah 25 cm. Tentukan panjang garis singgung
persekutuan dalam dari kedua lingkaran tersebut.