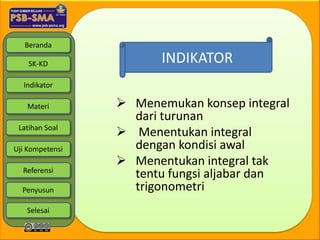
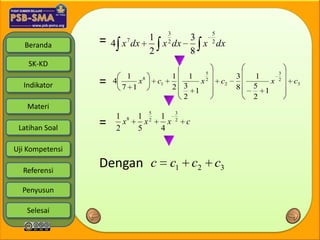
Dokumen tersebut membahas tentang integral dan penerapannya dalam memecahkan masalah, khususnya terkait perancangan bangunan tinggi. Integral digunakan untuk menentukan rancangan bagian atas dan bawah bangunan agar tahan terhadap angin yang semakin kuat di bagian atas. Dokumen ini juga berisi pengertian integral, rumus-rumus dasar, sifat-sifat, dan contoh soal integral.

1. 1

2. Beranda
Mengapa Belajar Integral
SK-KD
Lihatlah gedung-gedung pencakar
Indikator langit yang ada di Jakarta, atau
Petronas di Kuala Lumpur.
Materi
Semakin tinggi bangunan semakin
Latihan Soal kuat angin yang menghantamnya.
Karenanya bagian atas bangunan
Uji Kompetensi harus dirancang berbeda dengan
bagian bawah.
Untuk menentukan rancangan
Referensi
yang tepat, digunakan
perhitungan integral.
Penyusun
Selesai

3. Beranda
SK-KD
STANDAR KOMPETENSI
Indikator
1. Menggunakan konsep integral
Materi dalam pemecahan masalah
Latihan Soal
KOMPETENSI DASAR
Uji Kompetensi
Referensi 1.1 Memahami konsep integral
tak tentu dan integral tentu
Penyusun
Selesai

4. Beranda
SK-KD INDIKATOR
Indikator
Materi  Menemukan konsep integral
dari turunan
Latihan Soal
 Menentukan integral
Uji Kompetensi dengan kondisi awal
 Menentukan integral tak
Referensi
tentu fungsi aljabar dan
Penyusun trigonometri
Selesai

5. Beranda
PENGERTIAN INTEGRAL
SK-KD
Integral merupakan kebalikan dari
Indikator
turunan (diferensial). Integral disebut juga
Materi sebagai anti diferensial.
Latihan Soal Notasi Integral dan Integral tak Tentu
Uji Kompetensi
adalah
Referensi
Dibaca: integral dari f(x) terhadap variabel x
Penyusun
Selesai

6. Beranda
PENGERTIAN INTEGRAL
SK-KD
• Secara umum himpunan semua anti
Indikator difrensial dari fungsi f(x) dirumuskan
sebagai :
Materi
f ( x)dx F ( x) c
Latihan Soal
Uji Kompetensi
f(x) = integran
F(x) = fungsi integral atau fungsi primitif
Referensi x = variabel
c = konstanta integrasi
Penyusun
Selesai

7. Beranda
SK-KD
RUMUS-RUMUS INTEGRAL
Indikator n 1 +1
∫x dx = + c , dengan n≠ -1
+1
Materi
Latihan Soal n a +1
∫ ax
x dx =
+1 + c , dengan n≠ -1
Uji Kompetensi
Referensi ∫a x
dx = +c
Penyusun
Selesai

8. Beranda SIFAT-SIFAT INTEGRAL
SK-KD
Indikator a. f ( x) g ( x) dx f ( x)dx g ( x)dx
Materi b.
f ( x) g ( x) dx f ( x)dx g ( x)dx
Latihan Soal
c. a f ( x)dx a f ( x)dx
Uji Kompetensi
1 dx
Referensi d. dx ln x c
x x
Penyusun e.
dx x c
Selesai

9. Beranda CONTOH : 1
SK-KD
Tentukan nilai integral tak tentu berikut:
Indikator
1. 3t 2dt
1 21
Materi Jawab: 3t 2 dt 3 t 2 dt 3. t c t3 c
2 1
Latihan Soal 1 3 3 5
7
2. 4x x2 x 2 dx
2 8
Uji Kompetensi Jawab:
3 5
Referensi 7 1 2 3 2
4x x x dx
2 8
Penyusun
3 5
7 1 2 3 2
4 x dx x dx x dx
Selesai 2 8

10. 1 3 5
= 3
Beranda 4 x 7 dx x 2 dx x 2 dx
2 8
SK-KD
5 3
1 1 1 3 1
Indikator = 4
7 1
x 8
c1
2 3 1
x2 c2
8 5
x 2
c3
1
2 2
Materi
1 8 1 5 1 3
Latihan Soal
= 2
x
5
x2
4
x 2
c
Uji Kompetensi
Referensi
Dengan c c1 c2 c3
Penyusun
Selesai

11. Beranda
Menentukan f(x) jika diketahui
SK-KD
f’(x) dan f(a) dengan a=konstanta
Indikator
Materi
• Untuk menentukan f(x) dengan cara:
Latihan Soal a. f ( x) f ' ( x) dx
Uji Kompetensi b. Tentukan a dengan mensubstitusikan
pada f(x), yaitu f(a)
Referensi
c. Tentukan f(x)
Penyusun
Selesai

12. Beranda CONTOH : 2
SK-KD
1 3 2
Tentukan f(x) jika diketahui: f' x
3
x dan f (2)
Indikator 3
Jawab: f ( x) f ' ( x)dx
Materi
1
1 3 1 4
x dx = 3 x3 1 x c
Latihan Soal
3 3 1
c = 12
Uji Kompetensi 2 2 16
f (2) c c 2
3 3 12
Referensi
1 4
Jadi f ( x) x 2
Penyusun 12
Selesai

13. Beranda SOAL LATIHAN
SK-KD
Tentukan nilai integral berikut.
Indikator 1. 3x 2 4 x dx
5 2
Materi 2. 8 dx
x3 x 2
3. 2t 1 t 2 dt
Latihan Soal
4.
3 sin xdx
Uji Kompetensi 5.
2 sin 2 x cos x dx
Referensi
Tentukan f(x) jika diketahui:
Penyusun 6. f ' ( x) 8x 2 dan f (5) 36
3
7. f ' ( x) x 1 x 2 dan f ( 3)
Selesai 2

14. Beranda
SK-KD UJI KOMPETENSI
Indikator
Materi
Latihan Soal Klik disini
Uji Kompetensi
Referensi
Penyusun
Selesai

15. Beranda
REFERENSI
SK-KD
• Pesta E.S, Cecep Anwar, matematika
Indikator
Aplikasi Jilid, BSE, Pusat Perbukuan
Depdiknas, 2008
Materi
• Marten Kanginan. Matematika untuk
Latihan Soal
kelas XII semester 1, Grapindo
Bandung, 2006
Uji Kompetensi • Bob Foster, Soal UMPTN Matematika
IPA, Erlangga Bandung, 1996
Referensi
Penyusun
Selesai

16. Beranda PENYUSUN
SK-KD
Deny Asiah
Indikator Guru SMA Negeri 3
Kota Bengkulu
Materi Email: denyasiah@yahoo.co.id
Latihan Soal Editor :
Ali Tamami
Uji Kompetensi
Guru SMA Negeri 3 Sidoarjo
Referensi
Email : alijokam@yahoo.com
Penyusun
Selesai

17. Terima
Beranda
SK-KD
Kasih
Indikator
Materi
Selamat
Latihan Soal
Uji Kompetensi
Belajar
Referensi
Penyusun
Selesai

18. Beranda LISENSI
SK-KD
Indikator
Materi
Latihan Soal
Uji Kompetensi
Referensi
Penyusun
Selesai