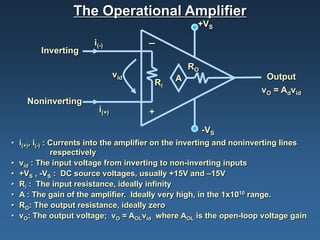
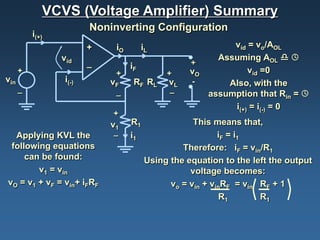
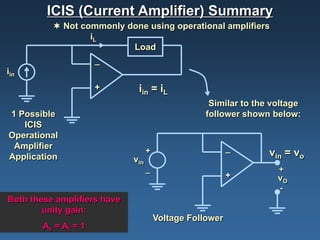
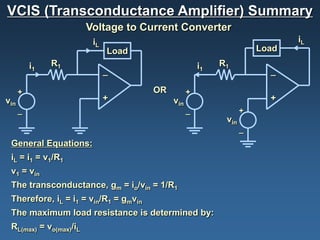
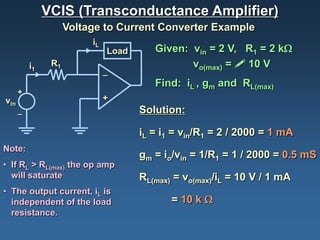
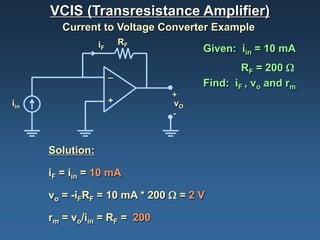
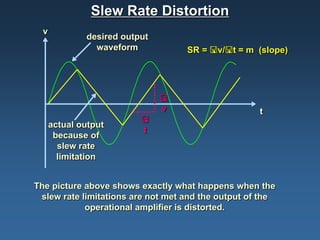
Operational amplifiers, or op amps, are devices that amplify input voltages or currents to produce larger output signals. They have very high gain and are used to build analog circuits. The four main types are voltage amplifiers, current amplifiers, transconductance amplifiers, and transresistance amplifiers. Voltage amplifiers, also called voltage controlled voltage sources (VCVS), can be configured non-inverting or inverting. In a non-inverting configuration, the output voltage is equal to the input voltage plus the input voltage multiplied by the feedback resistance. In an inverting configuration, the output voltage is equal to the negative input voltage multiplied by the feedback resistance divided by the input resistance.

1. Operational Amplifiers
Tutorial Series
_
+
Kristin Ackerson, Virginia Tech EE
Spring 2002 – VTech –Calvin Project

2. Table of Contents
The Operational Amplifier______________________________slides 3-4
The Four Amplifier Types______________________________slide 5
VCVS(Voltage Amplifier) Summary:
Noninverting Configuration____________slides 6-9
Inverting Configuration________________slides 10-12
ICIC(Current Amplifier) Summary________________________slide 13
VCIS (Transconductance Amplifier) Summary_____________slides 14-15
ICVS (Transresistance Amplifier) Summary_______________slides 16-18
Power Bandwidth_____________________________________slide 19
Slew Rate____________________________________________slide 20
Slew Rate Output Distortion____________________________ slide 21
Noise Gain___________________________________________slide 22
Gain-Bandwidth Product_______________________________slide 23
Cascaded Amplifiers - Bandwidth________________________slide 24
Common Mode Rejection Ratio__________________________slides 25-26
Power Supply Rejection Ratio___________________________slide 27
Sources_____________________________________________slide 28

3. The Operational Amplifier
• Usually Called Op Amps
• An amplifier is a device that accepts a varying input signal and
produces a similar output signal with a larger amplitude.
• Usually connected so part of the output is fed back to the input.
(Feedback Loop)
• Most Op Amps behave like voltage amplifiers. They take an input
voltage and output a scaled version.
• They are the basic components used to build analog circuits.
• The name “operational amplifier” comes from the fact that they were
originally used to perform mathematical operations such as
integration and differentiation.
• Integrated circuit fabrication techniques have made high-
performance operational amplifiers very inexpensive in comparison
to older discrete devices.

4. The Operational Amplifier
+VS
i(-) _
Inverting
RO
vid A Output
Ri
vO = Advid
Noninverting
i(+) +
-VS
• i(+), i(-) : Currents into the amplifier on the inverting and noninverting lines
respectively
• vid : The input voltage from inverting to non-inverting inputs
• +VS , -VS : DC source voltages, usually +15V and –15V
• Ri : The input resistance, ideally infinity
• A : The gain of the amplifier. Ideally very high, in the 1x1010 range.
• RO: The output resistance, ideally zero
• vO: The output voltage; vO = AOLvid where AOL is the open-loop voltage gain

5. The Four Amplifier Types
Gain Transfer
Description Symbol Function
Voltage Amplifier
or Av vo/vin
Voltage Controlled Voltage Source (VCVS)
Current Amplifier
or Ai io/iin
Current Controlled Current Source (ICIS)
Transconductance Amplifier
gm
or io/vin
(siemens)
Voltage Controlled Current Source (VCIS)
Transresistance Amplifier
rm
or vo/iin
(ohms)
Current Controlled Voltage Source (ICVS)

6. VCVS (Voltage Amplifier) Summary
Noninverting Configuration
i(+)
+ iO iL vid = vo/AOL
vid Assuming AOL  
_ iF +
+ + + vO vid =0
vin i(-) vF RF RL vL - Also, with the
_ _
_ assumption that Rin = 
i(+) = i(-) = 0
+
v1 R1 This means that,
Applying KVL the _ i1 iF = i 1
following equations Therefore: iF = vin/R1
can be found: Using the equation to the left the output
v1 = vin voltage becomes:
vO = v1 + vF = vin+ iFRF vo = vin + vinRF = vin RF + 1
R1 R1

7. VCVS (Voltage Amplifier) Summary
Noninverting Configuration Continued
The closed-loop voltage gain is symbolized by Av and is found to be:
Av = vo = RF + 1
vin R1
The original closed loop gain equation is:
Av = AF = AOL AF is the amplifier
1 + AOLβ gain with
feedback
Ideally AOL   , Therefore Av = 1
β
Note: The actual value of AOL is given for the specific device and
usually ranges from 50k  500k.
β is the feedback factor and by assuming open-loop gain is infinite:
β = R1
R1 + RF

8. VCVS (Voltage Amplifier) Summary
Noninverting Configuration Continued
Input and Output Resistance
Ideally, the input resistance for this configuration is infinity, but the a
closer prediction of the actual input resistance can be found with the
following formula:
RinF = Rin (1 + βAOL) Where Rin is given for the
specified device. Usually Rin is
in the MΩ range.
Ideally, the output resistance is zero, but the formula below gives a
more accurate value:
RoF = Ro Where Ro is given for the
βAOL + 1 specified device. Usually Ro is in
the 10s of Ωs range.

9. VCVS (Voltage Amplifier)
i(+)
Noninverting Configuration Example
+ iO iL
vid
Given: vin = 0.6V, RF = 200 kΩ
_ iF +
+ vO R1 = 2 kΩ , AOL = 400k
+ +
vin i(-) vF RF RL vL - Rin = 8 M Ω , Ro = 60 Ω
_ _ _
Find: vo , iF , Av , β , RinF and RoF
+
v1 R1
_ i1
Solution:
vo = vin + vinRF = 0.6 + 0.6*2x105 = 60.6 V iF = vin = 0.6 = 0.3 mA
R1 2000 R1 2000
Av = RF + 1 = 2x105 + 1 = 101 β = 1 = 1 = 9.9x10-3
R1 2000 AOL 101
RinF = Rin (1 + βAOL) = 8x106 (1 + 9.9x10-3*4x105) = 3.1688x1010 Ω
RoF = Ro = 60 = 0.015 Ω
βAOL + 1 9.9x10-3*4x105 + 1

10. VCVS (Voltage Amplifier) Summary
Inverting Configuration
RF The same
iF
assumptions used to
R1 find the equations for
i1
_ the noninverting
configuration are
+ + also used for the
vin + vO inverting
_ RL - configuration.
General Equations:
i1 = vin/R1
iF = i 1
vo = -iFRF = -vinRF/R1
Av = RF/R1 β = R1/RF

11. VCVS (Voltage Amplifier) Summary
Inverting Configuration Continued
Input and Output Resistance
Ideally, the input resistance for this configuration is equivalent to R1.
However, the actual value of the input resistance is given by the
following formula:
Rin = R1 + RF
1 + AOL
Ideally, the output resistance is zero, but the formula below gives a
more accurate value:
RoF = Ro
1 + βAOL
Note: β= R1 This is different from the equation used
R1 + RF on the previous slide, which can be confusing.

12. VCVS (Voltage Amplifier)
Inverting Configuration Example
iF RF
Given: vin = 0.6 V, RF = 20 kΩ
i1 R1
R1 = 2 kΩ , AOL = 400k
+
Rin = 8 M Ω , Ro = 60 Ω
+ _ +
vin vO Find: vo , iF , Av , β , RinF and RoF
_ RL -
Solution:
vo = -iFRF = -vinRF/R1 = -(0.6*20,000)/2000 = 12 V
iF = i1 = vin/R1 = 1 / 2000 = 0.5 mA
Av = RF/R1 = 20,000 / 2000 = 10 β = R1/RF = 2000 / 20,000 = 0.1
Rin = R1 + RF = 2000 + 20,000 = 2,000.05 Ω
1 + AOL 1 + 400,000
RoF = Ro = 60 = 1.67 m Ω
1 + βAOL 1 + 0.09*400,000 Note: β is 0.09 because using
different formula than above

13. ICIS (Current Amplifier) Summary
 Not commonly done using operational amplifiers
iL
Load
_
iin
+ iin = iL
Similar to the voltage
1 Possible follower shown below:
ICIS
Operational
Amplifier _
+ vin = vo
Application vin
_ +
+ vO
-
Both these amplifiers have
unity gain:
Voltage Follower
Av = Ai = 1

14. VCIS (Transconductance Amplifier) Summary
Voltage to Current Converter
iL iL
Load Load
i1 R1 i1 R1
_ _
+ OR +
vin + vin +
_ _ +
vin
_
General Equations:
iL = i1 = v1/R1
v1 = vin
The transconductance, gm = io/vin = 1/R1
Therefore, iL = i1 = vin/R1 = gmvin
The maximum load resistance is determined by:
RL(max) = vo(max)/iL

15. VCIS (Transconductance Amplifier)
Voltage to Current Converter Example
iL
Load Given: vin = 2 V, R1 = 2 kΩ
i1 R1 vo(max) =  10 V
_
Find: iL , gm and RL(max)
+
vin +
_ Solution:
iL = i1 = vin/R1 = 2 / 2000 = 1 mA
Note:
gm = io/vin = 1/R1 = 1 / 2000 = 0.5 mS
• If RL > RL(max) the op amp
will saturate RL(max) = vo(max)/iL = 10 V / 1 mA
• The output current, iL is
independent of the load = 10 k Ω
resistance.

16. VCIS (Transresistance Amplifier) Summary
Current to Voltage Converter
iF RF
_
+
iin + vO
-
General Equations:
iF = iin
vo = -iFRF
rm = vo/iin = RF

17. VCIS (Transresistance Amplifier) Summary
Current to Voltage Converter
• Transresistance Amplifiers are used for low-power
applications to produce an output voltage proportional to
the input current.
• Photodiodes and Phototransistors, which are used in the
production of solar power are commonly modeled as
current sources.
• Current to Voltage Converters can be used to convert these
current sources to more commonly used voltage sources.

18. VCIS (Transresistance Amplifier)
Current to Voltage Converter Example
iF RF
Given: iin = 10 mA
RF = 200 Ω
_
Find: iF , vo and rm
+
iin + vO
-
Solution:
iF = iin = 10 mA
vo = -iFRF = 10 mA * 200 Ω = 2 V
rm = vo/iin = RF = 200

19. Power Bandwidth
The maximum frequency at which a sinusoidal output signal can be
produced without causing distortion in the signal.
The power bandwidth, BWp is determined using the desired
output signal amplitude and the the slew rate (see next slide)
specifications of the op amp.
BWp = SR
2πVo(max)
SR = 2πfVo(max) where SR is the slew rate
Example:
Given: Vo(max) = 12 V and SR = 500 kV/s
Find: BWp
Solution: BWp = 500 kV/s = 6.63 kHz
2π * 12 V

20. Slew Rate
A limitation of the maximum possible rate of change of the
output of an operational amplifier.
As seen on the previous slide, This is derived from:
SR = 2πfVo(max) SR = vo/tmax
 f is the
frequency in Slew Rate is independent of the
Hz closed-loop gain of the op amp.
Example:
Given: SR = 500 kV/s and vo = 12 V (Vo(max) = 12V)
Find: The t and f.
Solution: t = vo / SR = (10 V) / (5x105 V/s) = 2x10-5 s
f = SR / 2πVo(max) = (5x105 V/s) / (2π * 12) = 6,630 Hz

21. Slew Rate Distortion
v
desired output
waveform SR = v/t = m (slope)

v t

actual output
t
because of
slew rate
limitation
The picture above shows exactly what happens when the
slew rate limitations are not met and the output of the
operational amplifier is distorted.

22. Noise Gain
The noise gain of an amplifier is independent of the amplifiers
configuration (inverting or noninverting)
The noise gain is given by the formula:
AN = R1 + RF
R1
Example 1: Given a noninverting amplifier with the resistance
values, R1 = 2 kΩ and RF = 200 kΩ
Find: The noise gain.
AN = 2 kΩ + 200 kΩ = 101  Note: For the
2 kΩ noninverting amplifier AN = AV
Example 2: Given an inverting amplifier with the resistance
values, R1 = 2 kΩ and RF = 20 kΩ
Find: The noise gain.
AN = 2 kΩ + 20 kΩ = 12  Note: For the
2 kΩ inverting amplifier AN > AV

23. Gain-Bandwidth Product
In most operational amplifiers, the open-loop gain begins
dropping off at very low frequencies. Therefore, to make the
op amp useful at higher frequencies, gain is traded for
bandwidth.
The Gain-Bandwidth Product (GBW) is given by:
GBW = ANBW
Example: For a 741 op amp, a noise gain of 10 k corresponds
to a bandwidth of ~200 Hz
Find: The GBW
GBW = 10 k * 200 Hz = 2 MHz

24. Cascaded Amplifiers - Bandwidth
Quite often, one amplifier does not increase the signal enough
and amplifiers are cascaded so the output of one amplifier is the
input to the next.
The amplifiers are matched so:
BWS = BW1 = BW2 = GBW where, BWS is the bandwidth of all
AN the cascaded amplifiers and AN is
the noise gain
The Total Bandwidth of the Cascaded Amplifiers is:
BWT = BWs(21/n – 1)1/2 where n is the number of amplifiers
that are being cascaded
Example: Cascading 3 Amplifiers with GBW = 1 MHz and AN = 15,
Find: The Total Bandwidth, BWT
BWS = 1 MHz / 15 = 66.7 kHz
BWT = 66.7 kHz (21/3 – 1)1/2 = 34 kHz

25. Common-Mode Rejection Ratio
The common-mode rejection ratio (CMRR) relates to the ability of
the op amp to reject common-mode input voltage. This is very
important because common-mode signals are frequently
encountered in op amp applications.
CMRR = 20 log|AN / Acm|
Acm = AN
log-1 (CMRR / 20)
We solve for Acm because Op Amp data sheets list the CMRR value.
The common-mode input voltage is an average of the voltages that
are present at the non-inverting and inverting terminals of the
amplifier.
vicm = v(+) + v(-)
2

26. Common-Mode Rejection Ratio
Example
Given: A 741 op amp with CMRR = 90 dB and a noise gain,
AN = 1 k
Find: The common mode gain, Acm
Acm = AN = 1000
log-1 (CMRR / 20) log-1 (90 / 20)
= 0.0316
It is very desirable for the common-mode gain to be small.

27. Power Supply Rejection Ratio
One of the reasons op amps are so useful, is that they can
be operated from a wide variety of power supply voltages.
The 741 op amp can be operated from bipolar supplies
ranging from 5V to 18V with out too many changes to
the parameters of the op amp.
The power supply rejection ratio (SVRR) refers to the slight
change in output voltage that occurs when the power
supply of the op amp changes during operation.
SVRR = 20 log (Vs / Vo)
The SVRR value is given for a specified op amp. For the
741 op amp, SVRR = 96 dB over the range 5V to 18V.

28. Open-Loop Op Amp Characteristics
Table 12.11
Device LM741C LF351 OP-07 LH0003 AD549K
Hybrid
Technology BJT BiFET BJT BiFET
BJT
AOL(typ) 200 k 100 k 400 k 40 k 100 k
Rin 2 MΩ 1012 Ω 8 MΩ 100 kΩ 1013 Ω || 1 pF
Ro 50 Ω 30 Ω 60 Ω 50 Ω ~100 Ω
SR 0.5 V/µs 13 V/µs 0.3 V/µs 70 V/µs 3 V/µs
CMRR 90 dB 100 dB 110 dB 90 dB 90 dB

29. Sources
Dailey, Denton. Electronic Devices and Circuits, Discrete and Integrated. Prentice Hall, New
Jersey: 2001. (pp 456-509)
1Table 12.1: Selected Op Amps and Their Open Loop Characteristics, pg 457
Liou, J.J. and Yuan, J.S. Semiconductor Device Physics and Simulation. Plenum Press,
New York: 1998.
Neamen, Donald. Semiconductor Physics & Devices. Basic Principles. McGraw-Hill,
Boston: 1997. (pp 351-357)
Web Sources
www.infoplease.com/ce6/sci/A0803814.html
http://www.infoplease.com/ce6/sci/A0836717.html
http://people.msoe.edu/~saadat/PSpice230Part3.htm