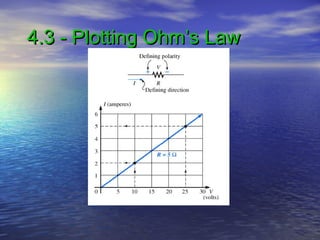
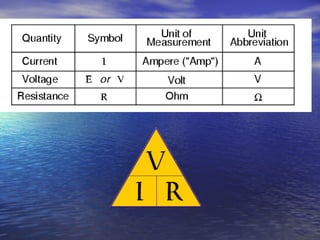
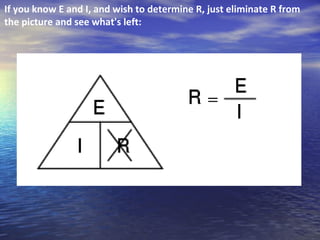
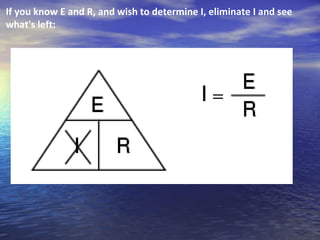
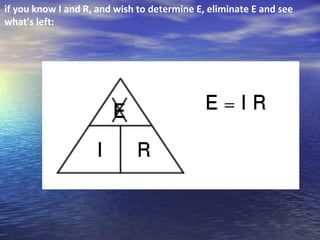
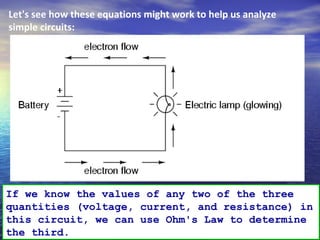
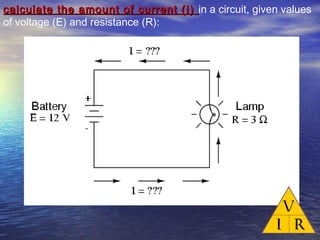
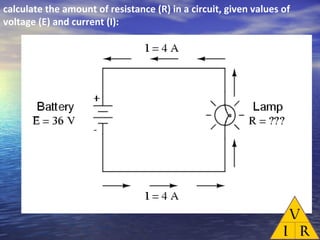
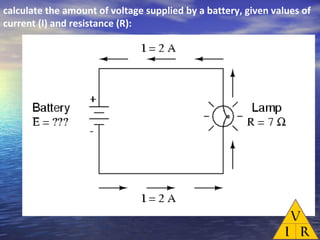
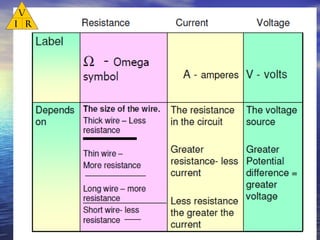
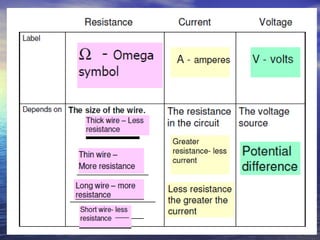
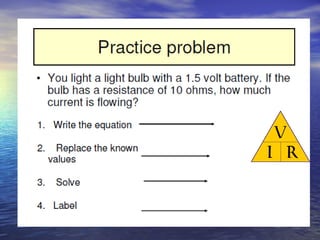
Ohm's law defines the relationship between voltage, current, and resistance in a circuit. It states that current is directly proportional to voltage and inversely proportional to resistance. The amount of current, voltage, or resistance in a circuit can be calculated if two of the three values are known using the equation: I = V/R Some key points about Ohm's law include: - Voltage is measured in volts (V), current in amps (A), and resistance in ohms (Ω) - Ohm's law can be rearranged to solve for any of the three circuit variables - Examples are provided to demonstrate calculating unknown values given two known values

1. Ohm's law magic triangle
Ohms law,
defines the relationship between voltage, current and
resistance.
The amount of current in a circuit in directly
proportional to the amount of voltage applied and
inversely proportional to the amount of resistance.
Expressed mathematically.
By : Sundas
Shabbir

2. Ohm’s LawOhm’s Law
WhereWhere:: I = current (amperes, A)I = current (amperes, A)
E = voltage (volts, V)E = voltage (volts, V)
R = resistance (ohms,R = resistance (ohms,
ΩΩ))
R
E
I =

3. 4.3 - Plotting Ohm’s Law4.3 - Plotting Ohm’s Law

4. Voltage measured in volts, symbolized by
the letters "E" or "V".
Current measured in amps, symbolized by
the letter "I".
Resistance measured in ohms, symbolized
by the letter "R".

6. If you know E and I, and wish to determine R, just eliminate R from
the picture and see what's left:

7. If you know E and R, and wish to determine I, eliminate I and see
what's left:

8. if you know I and R, and wish to determine E, eliminate E and see
what's left:

9. Let's see how these equations might work to help us analyze
simple circuits:
If we know the values of any two of the three
quantities (voltage, current, and resistance) in
this circuit, we can use Ohm's Law to determine
the third.

10. calculate the amount of current (I)calculate the amount of current (I) in a circuit, given values
of voltage (E) and resistance (R):

11. calculate the amount of resistance (R) in a circuit, given values of
voltage (E) and current (I):

12. calculate the amount of voltage supplied by a battery, given values of
current (I) and resistance (R):

13. • Example #1Example #1
• Find the current of an electrical circuit thatFind the current of an electrical circuit that
has resistance of 50 Ohms and voltagehas resistance of 50 Ohms and voltage
supply of 5 Volts.supply of 5 Volts.
• Solution:Solution:
• VV = 5V = 5V
• RR = 50Ω = 50Ω
• II = = V / RV / R = 5V / 50Ω = 0.1A = 100mA = 5V / 50Ω = 0.1A = 100mA

14. • Example #2Example #2
• Find the resistance of an electrical circuitFind the resistance of an electrical circuit
that has voltage supply of 10 Volts andthat has voltage supply of 10 Volts and
current of 5mA.current of 5mA.
• Solution:Solution:
• VV = 10V = 10V
• II = 5mA = 0.005A = 5mA = 0.005A
• RR = = V / IV / I = 10V / 0.005A = 2000Ω = 2kΩ = 10V / 0.005A = 2000Ω = 2kΩ

15. Electric PowerElectric Power
 The unit of electric power is the watt (W).one watt of power equals theThe unit of electric power is the watt (W).one watt of power equals the
work done in one second by one volt of potential difference in movingwork done in one second by one volt of potential difference in moving
one coulomb of charge.one coulomb of charge.
 Power is an indication of how much work (the conversionPower is an indication of how much work (the conversion
of energy from one form to another) can be done in aof energy from one form to another) can be done in a
specific amount of time; that is, aspecific amount of time; that is, a raterate of doing work.of doing work.
Power in watt = volt x amperes.Power in watt = volt x amperes.
P = V x I ,I = P/ V , V = P / IP = V x I ,I = P/ V , V = P / I
t
W
P =second/joule1(W)Watt1 =

16. Example of powerExample of power
 Energy (Energy (WW) lost or gained by any system) lost or gained by any system
is determined by:is determined by:
W =W = PtPt
 Since power is measured in watts (orSince power is measured in watts (or
joules per second) and time in seconds,joules per second) and time in seconds,
the unit of energy is thethe unit of energy is the wattsecondwattsecond (Ws)(Ws)
oror joulejoule (J)(J)

22. The force
or
pressure
behind
electricity

27. • Electric power definitionElectric power definition
• The electric power P is equal to the energyThe electric power P is equal to the energy
consumption E divided by the consumptionconsumption E divided by the consumption
time t:time t:
• Watt definitionWatt definition
• Watt is the unit of Watt is the unit of powerpower (symbol: W). (symbol: W).
• The watt unit is named after James Watt,The watt unit is named after James Watt,
the inventor of the steam engine.the inventor of the steam engine.
• One watt is defined as the energyOne watt is defined as the energy
consumption rate of one joule per second.consumption rate of one joule per second.

28. • 1W = 1J / 1s1W = 1J / 1s
• One watt is also defined as the currentOne watt is also defined as the current
flow of one ampere with voltage of oneflow of one ampere with voltage of one
volt.volt.
• 1W = 1V × 1A1W = 1V × 1A
• P is the electric power in watt (W).P is the electric power in watt (W).
• E is the energy consumption in joule (J).E is the energy consumption in joule (J).
• t is the time in seconds (s).t is the time in seconds (s).

29. • ExampleExample
• Find the electric power of an electricalFind the electric power of an electrical
circuit that consumes 120 joules for 20circuit that consumes 120 joules for 20
seconds.seconds.
• Solution:Solution:
• EE = 120J = 120J
• tt = 20s = 20s
• PP = = EE / / tt = 120J / 20s = 6W = 120J / 20s = 6W

30. • Electric power calculationElectric power calculation
• The power formula can be used in three ways:The power formula can be used in three ways:
• P= v x I OR P =IP= v x I OR P =I22
x R OR Px R OR P
= V= V22
/ R/ R
• P is the electric power in watt (W).P is the electric power in watt (W).
• V is the voltage in volts (V).V is the voltage in volts (V).
• I is the current in amps (A).I is the current in amps (A).
• R is the resistance in ohms (ΩR is the resistance in ohms (Ω
• I= P/VI= P/V
• V= P/IV= P/I

31. • Example 1Example 1: A toaster takes 10 A from the: A toaster takes 10 A from the
120v power line. How much power is120v power line. How much power is
used ?used ?
• Ans : P=V x I = 120v x 10 AAns : P=V x I = 120v x 10 A
• P=1200WP=1200W
• Exam 2Exam 2: how much current flows in the: how much current flows in the
filament of a 300 w bulb connected to thefilament of a 300 w bulb connected to the
120v power line?120v power line?
• Ans : I=P / V = 300w/120vAns : I=P / V = 300w/120v
• I= 2.5 AI= 2.5 A

32. • Multiple Units:Multiple Units:
• The basic units –ampere ,volt and ohmThe basic units –ampere ,volt and ohm
practical values in most electric power circuits,practical values in most electric power circuits,
but in many electronics application these unitsbut in many electronics application these units
are either too small or too big. Such as 2000kare either too small or too big. Such as 2000k
ohm resister value or 2000 v and 5 mA .ohm resister value or 2000 v and 5 mA .
• Example1: the I of 8 mA flows through a 5 kExample1: the I of 8 mA flows through a 5 k
ohms R. how much is the IR Voltage:ohms R. how much is the IR Voltage:
• Answer:Answer: V= IR 8V= IR 8 x10x10-3-3
x 5 xx 5 x101033
= 8 x 5= 8 x 5
• V=40 vV=40 v

33. • Example 2: How much current is produced by 60 vExample 2: How much current is produced by 60 v
across 12k ohms ?across 12k ohms ?
Answer : I = V/R 60/12 x 10Answer : I = V/R 60/12 x 1033
I = 5 x 10I = 5 x 10­3­3
=5 mA=5 mA
• Test point Question?,Test point Question?, 200w , 0.83A 1.8kw200w , 0.83A 1.8kw,,
1 An electric heater takes 15 A from the 120 V power1 An electric heater takes 15 A from the 120 V power
line .Calculate the Amount of power used.line .Calculate the Amount of power used.
2 How much is the load current for 100 W bulb2 How much is the load current for 100 W bulb
connected to the 120 V power line?connected to the 120 V power line?
3 How many watts is the power of 200 J/S equal to?3 How many watts is the power of 200 J/S equal to?

34. • Voltage DividerVoltage Divider
• Voltage divider rule finds the voltage overVoltage divider rule finds the voltage over
a load in electrical circuit, when the loadsa load in electrical circuit, when the loads
are connected in series.are connected in series.
• Voltage divider rule for DC circuitVoltage divider rule for DC circuit
• Voltage divider calculatorVoltage divider calculator
• Voltage divider rule for DC circuitVoltage divider rule for DC circuit

35. For a DC circuit with constant
voltage source VT
and resistors in
series, the voltage drop Vi
in
resistor Ri
is given by the formula:

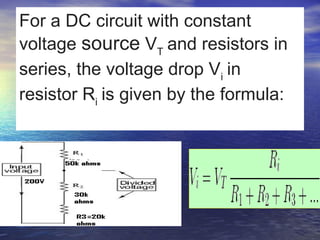
36. • VVi - voltage drop in resistor Ri in volts [V].i - voltage drop in resistor Ri in volts [V].
• VTVT - the equivalent voltage source or - the equivalent voltage source or
voltage drop in volts [V].voltage drop in volts [V].
• RRi - resistance of resistor i - resistance of resistor RRi in ohms [Ω].i in ohms [Ω].
• RR1 - resistance of resistor 1 - resistance of resistor RR1 in ohms [Ω].1 in ohms [Ω].
• RR2 - resistance of resistor 2 - resistance of resistor RR2 in ohms [Ω].2 in ohms [Ω].
• RR3 - resistance of resistor 3 - resistance of resistor RR3 in ohms [Ω].3 in ohms [Ω].

37. Example1.
Voltage source of VT
=30V is connected to
resistors in series, R1
=30Ω, R2
=40Ω.
Find the voltage drop on resistor R2
?
V2
= VT
× R2
/ (R1
+R2
) = 30V × 40Ω /
(30Ω+40Ω) = 17.14V

38. • Example2.Example2.
• Voltage source of VT=100V is connected toVoltage source of VT=100V is connected to
resistors in series, R1=50kΩ, R2=30kΩ, R3=20kresistors in series, R1=50kΩ, R2=30kΩ, R3=20k
Ω.Ω.
• Find the voltage drop on resistor R1,R2,R3.Find the voltage drop on resistor R1,R2,R3.

39. V3 Fine R3 volt drop
V3=R3/RT x VT= 20/100 X 200 V
V3=40 V
V2 Fine R2 volt drop
V2=R2/RT x VT= 30/100 X 200 V
V2=60 V
V1 Fine R1 volt drop
V1=R1/RT x VT= 50/100 X 200 V
V1=100 V.
The sum of V1,V2,V3 in series is 100+60+40=200v which
is equal to VT

40. Method of IR Drops:
V1=I x R1 =2mA x 50 kΩ= 100 v.
V2=I x R2 =2mA x 30 kΩ= 60 v.
V3=I x R3 =22mA x 20 kΩ= 40 v.

41. Series voltage divider with voltage taps.

42. voltage at tap point C.
vc=R4/RT X VT
=1 kΩ /20 kΩ X 24V
VC= 1.2 V.
Voltage at tap pint B.
VB=R3+R4/RT x VT
=1.5 kΩ +1 kΩ / 20 kΩ x 24v
VB= 3V.
Voltage at tap pint A.
VA=R2+R3+R4/RT x VT
=7.5kΩ +1.5 kΩ +1 kΩ / 20 kΩ x
24v
VA= 12.6V.

43. Current Divider with two parallel
resistances.
It is often necessary to find the individual
branch currents in a bank from the
resistances and IT , but without knowing the
voltage across the bank this problem can
be solved by using the fact that currents
divide inversely as the branch resistances.
such as show in example:

44. Current divider with two branch resistances each
branch I is inversely proportional to its R. the
small R has more I.
Calculation: I1 =R2/R1+R2 x IT
I1 = 4/2+4 x30
I1 = 20 A
Calculation: for other branch I2 =R1/R1+R2 x IT
I2 = 2/2+4 =30
I2 = 10 A