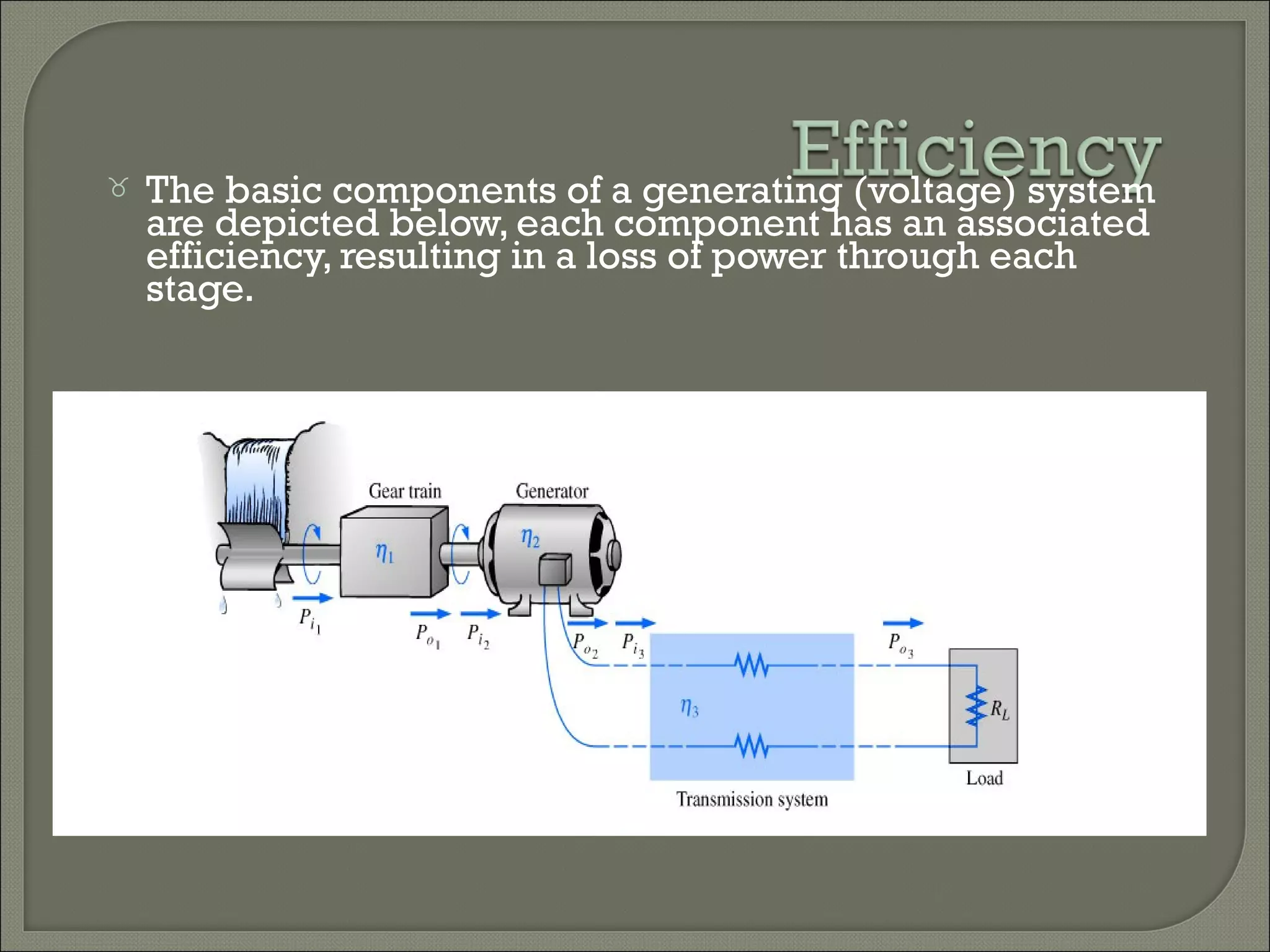
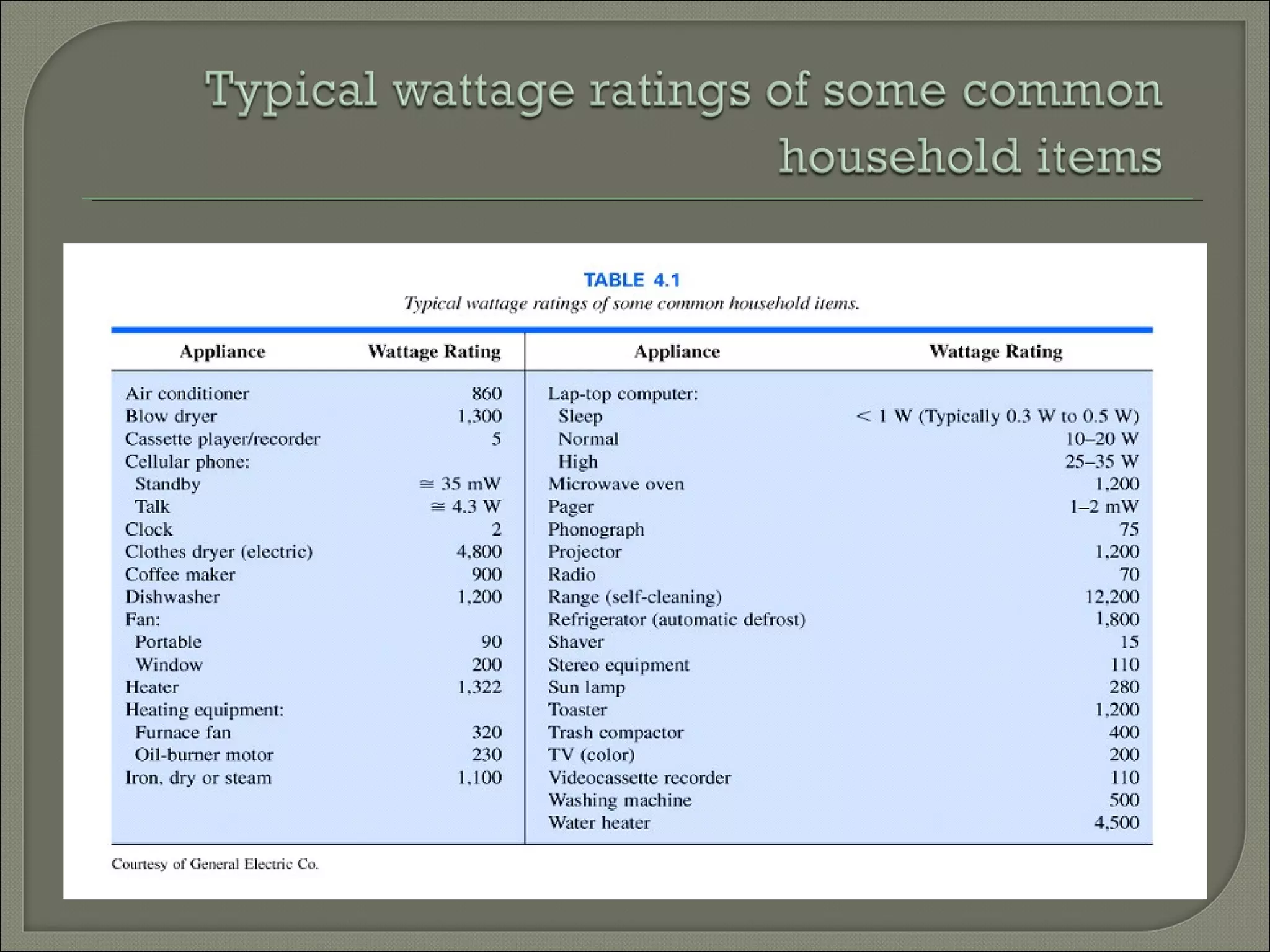
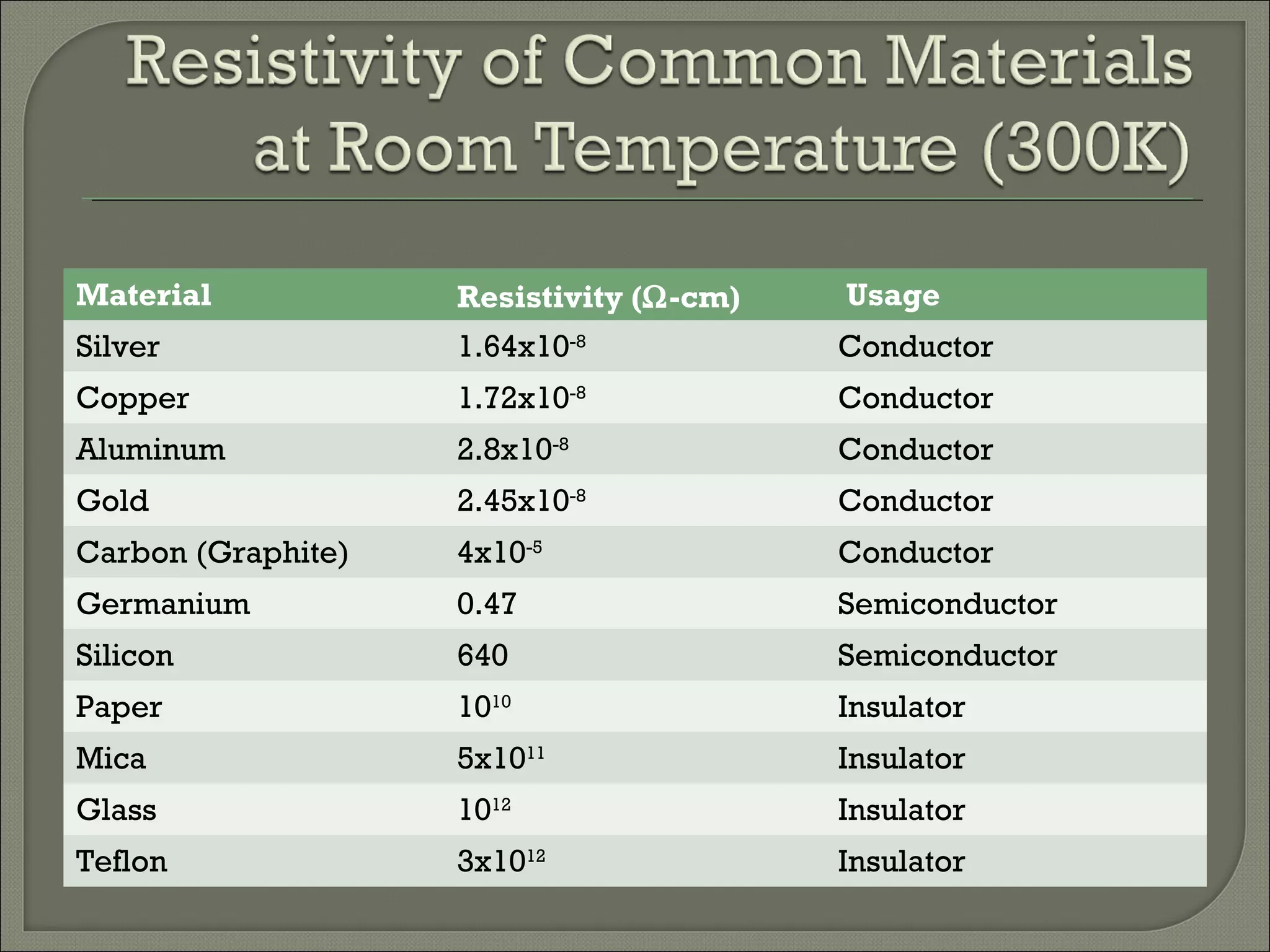
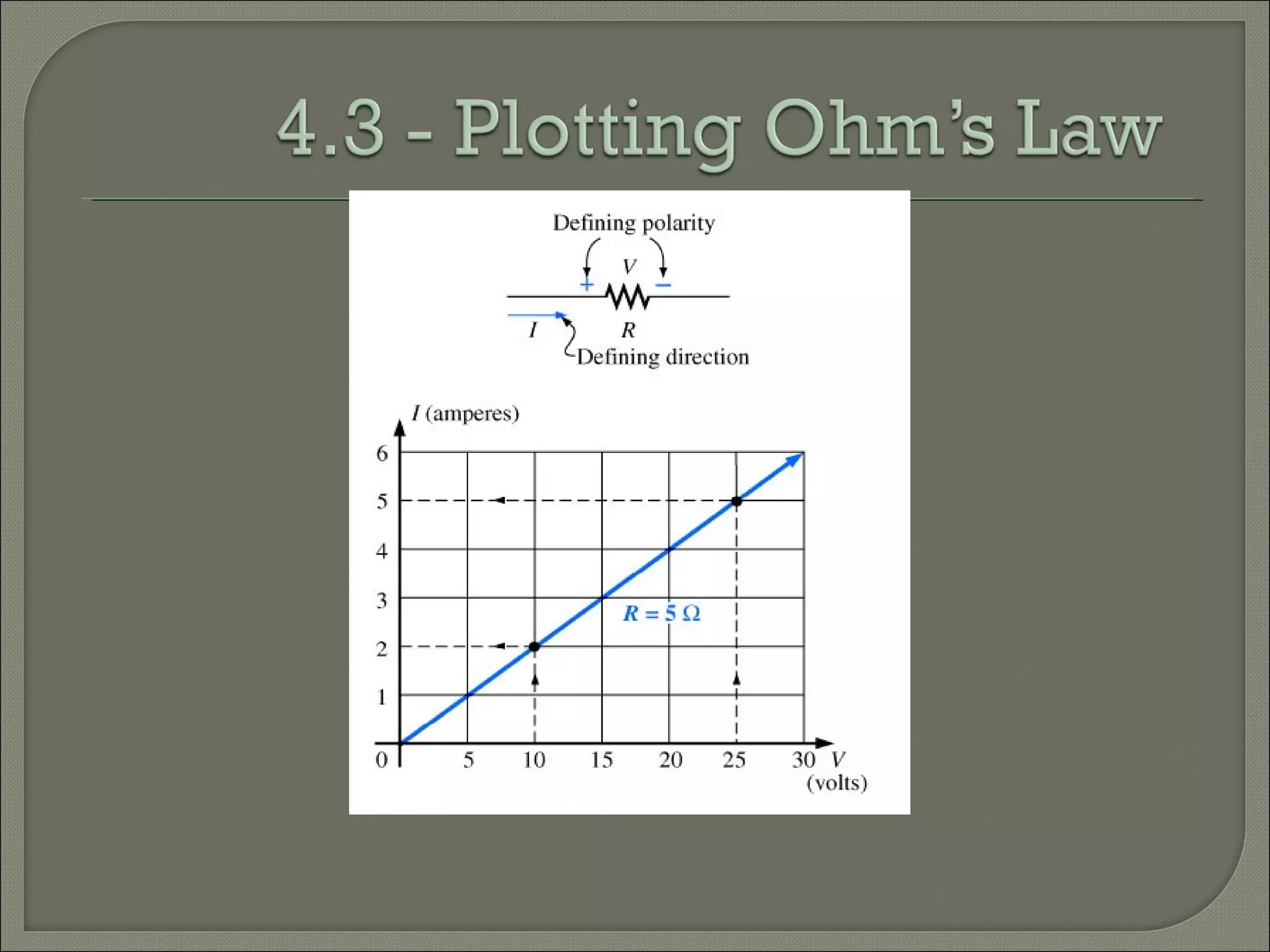
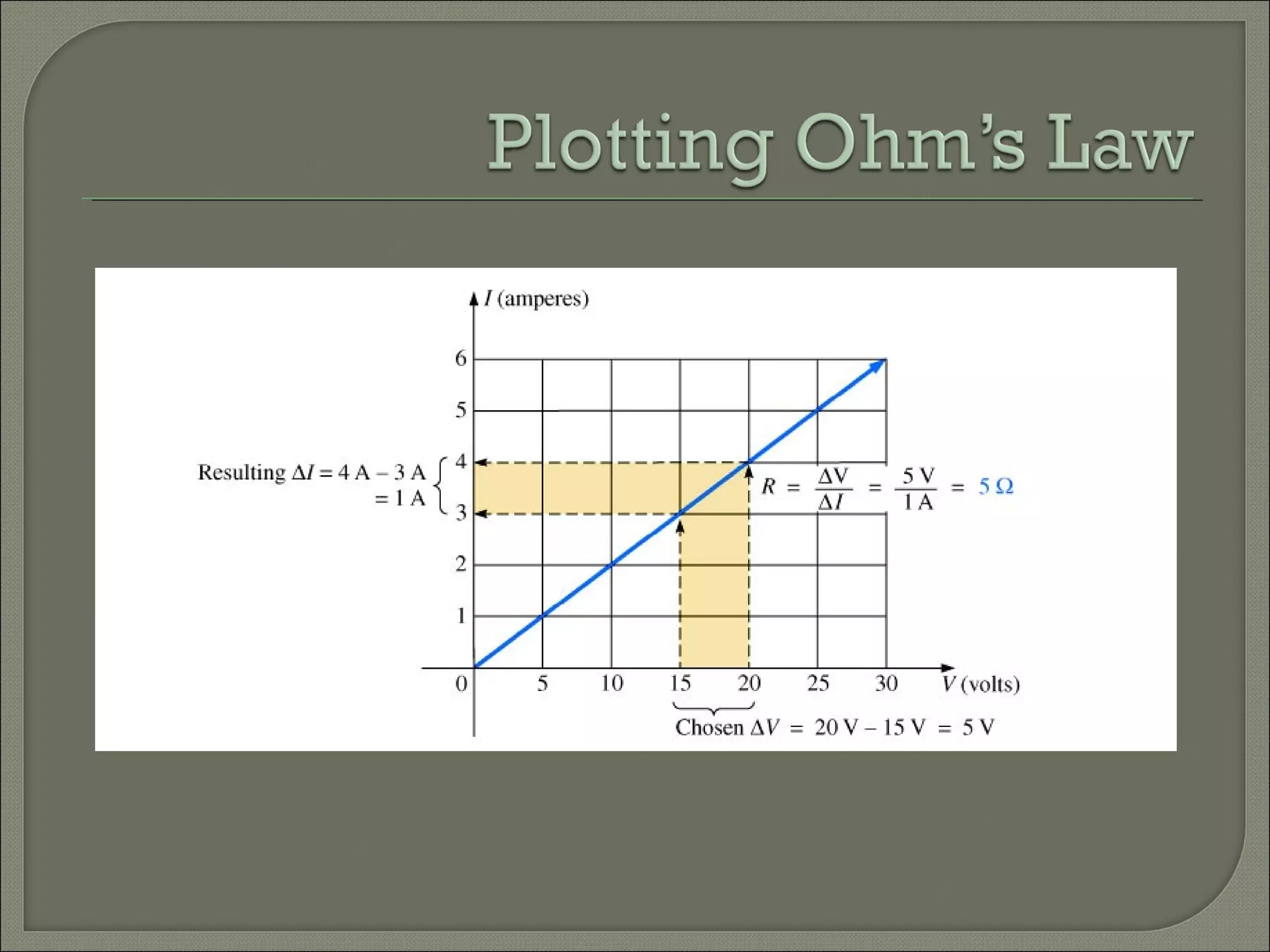
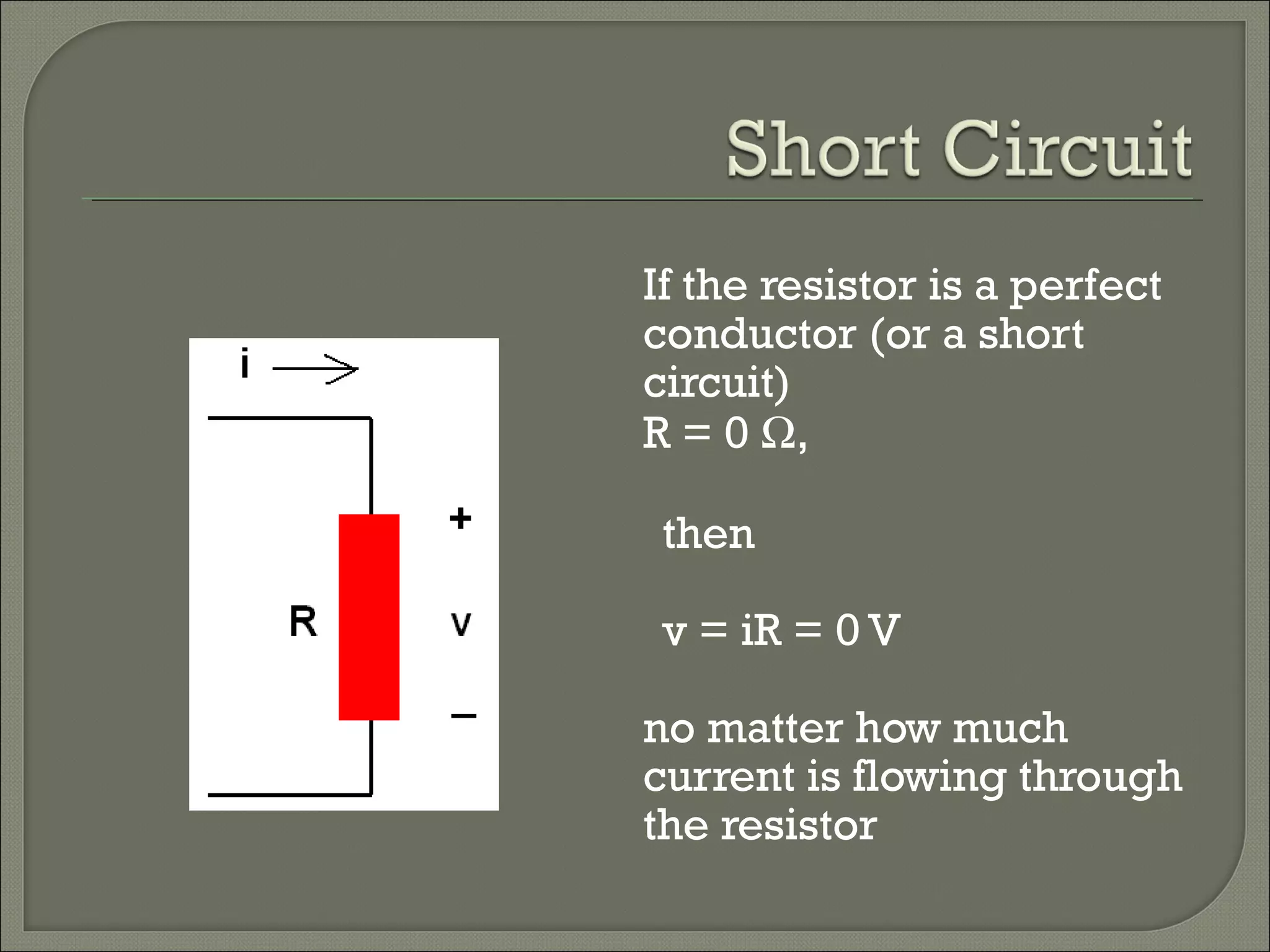
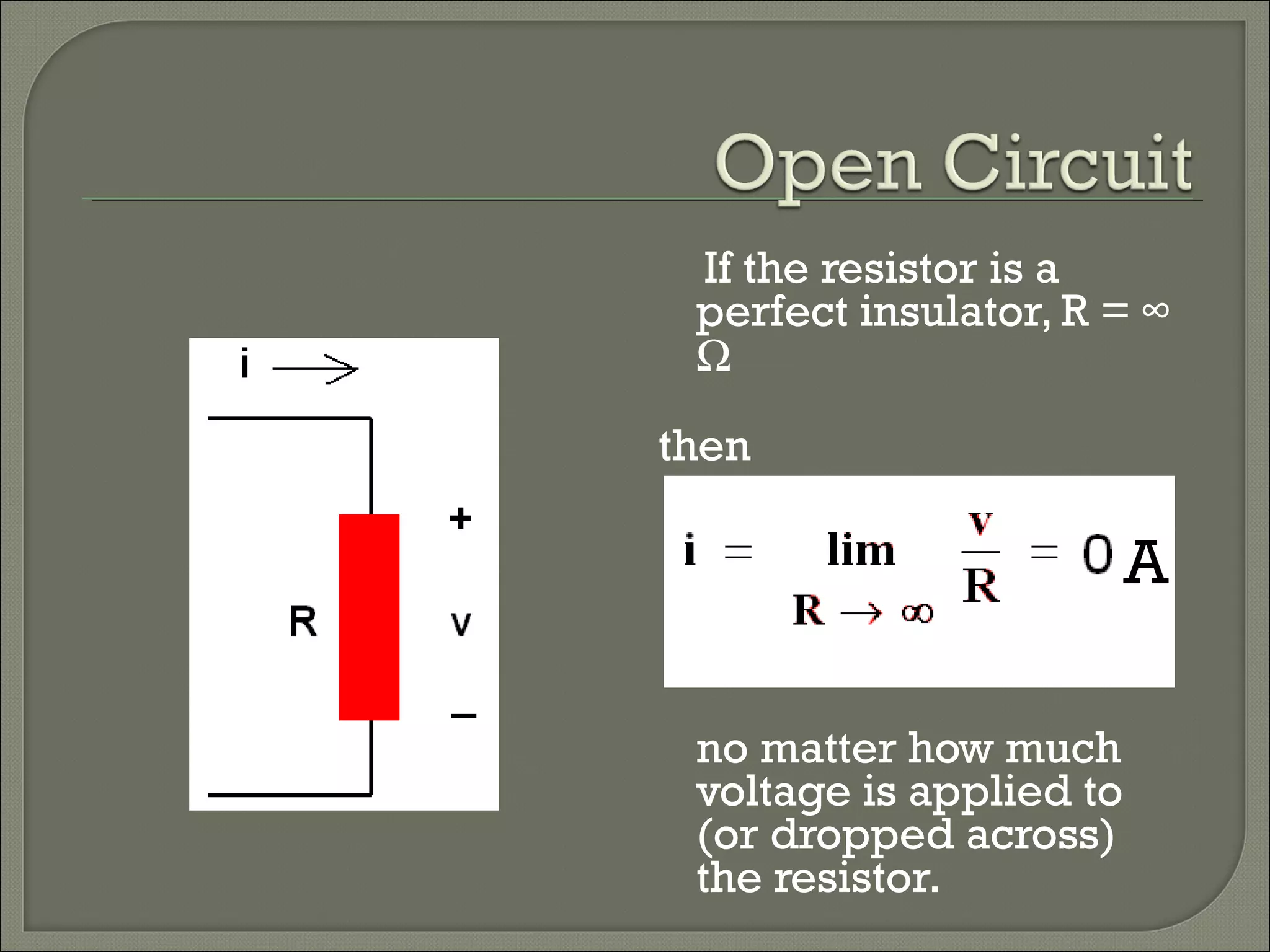
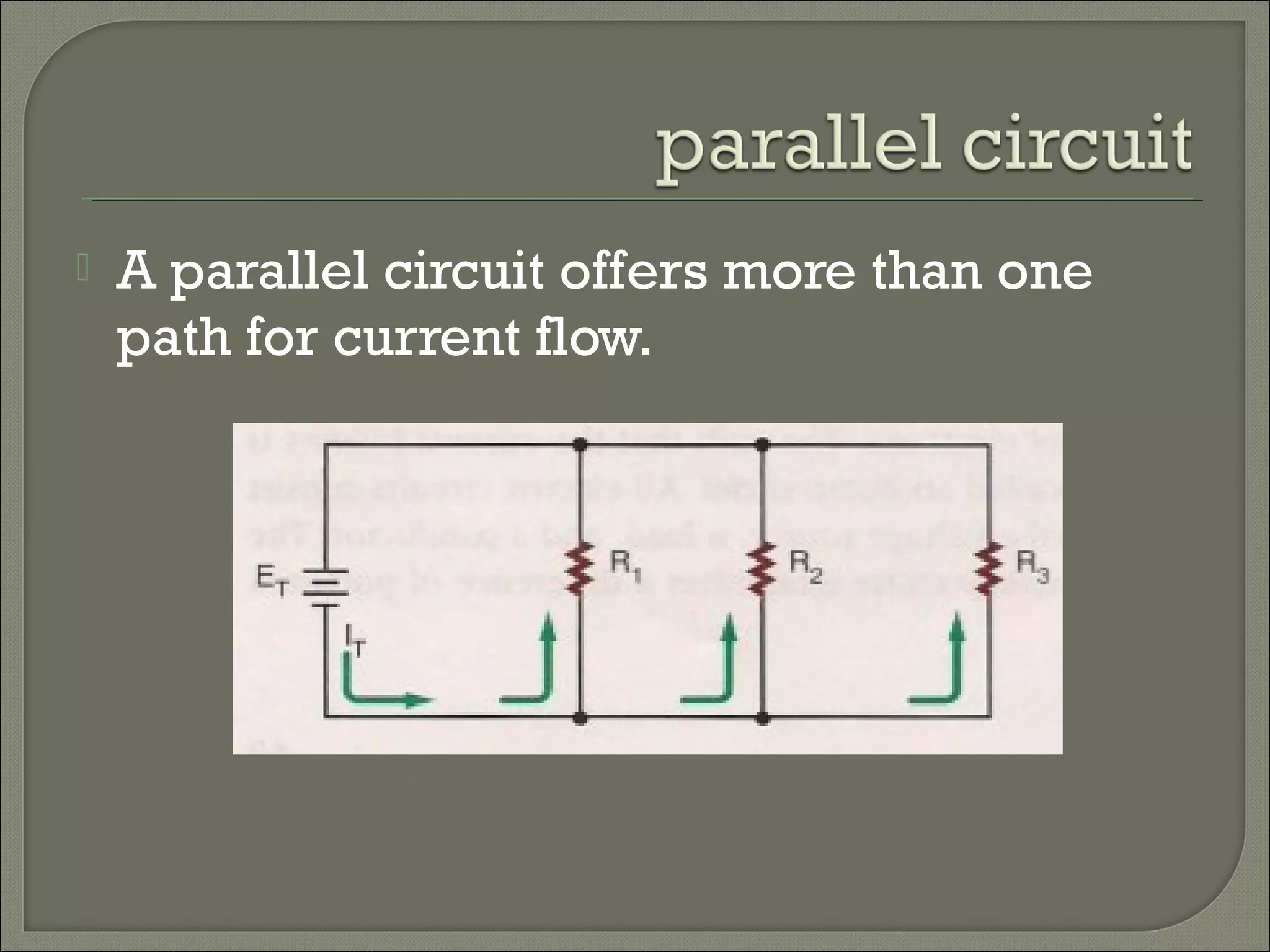
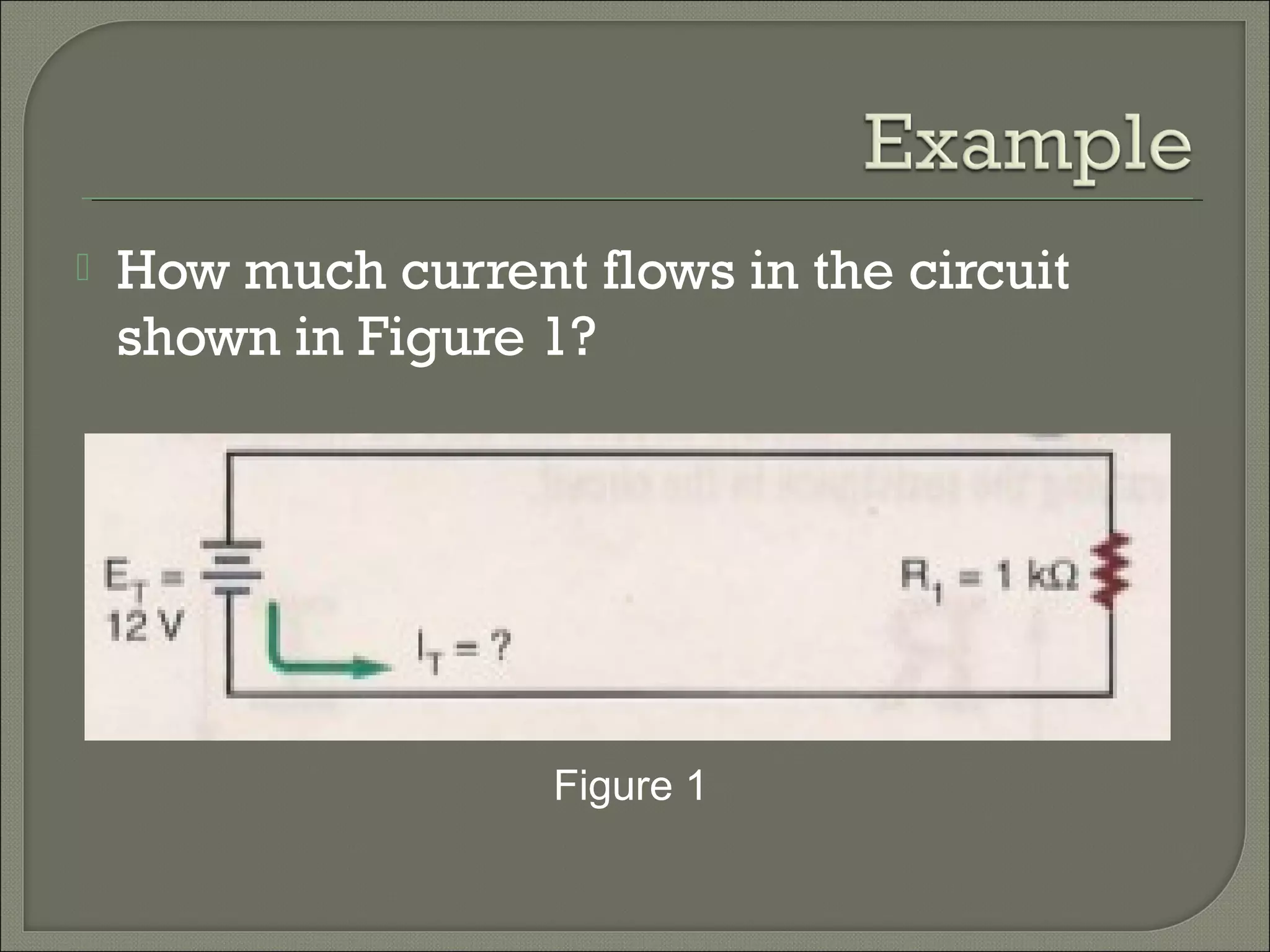
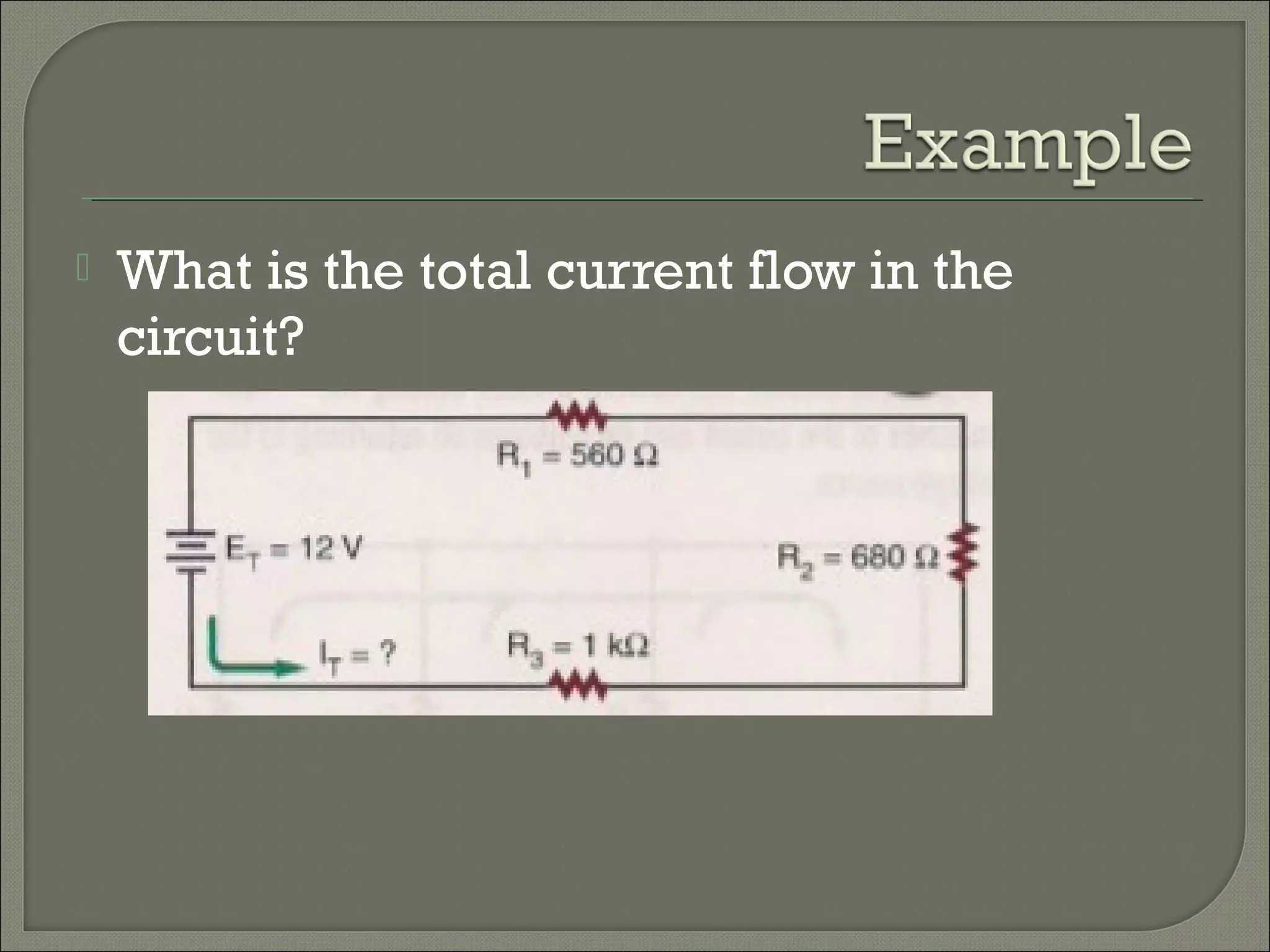
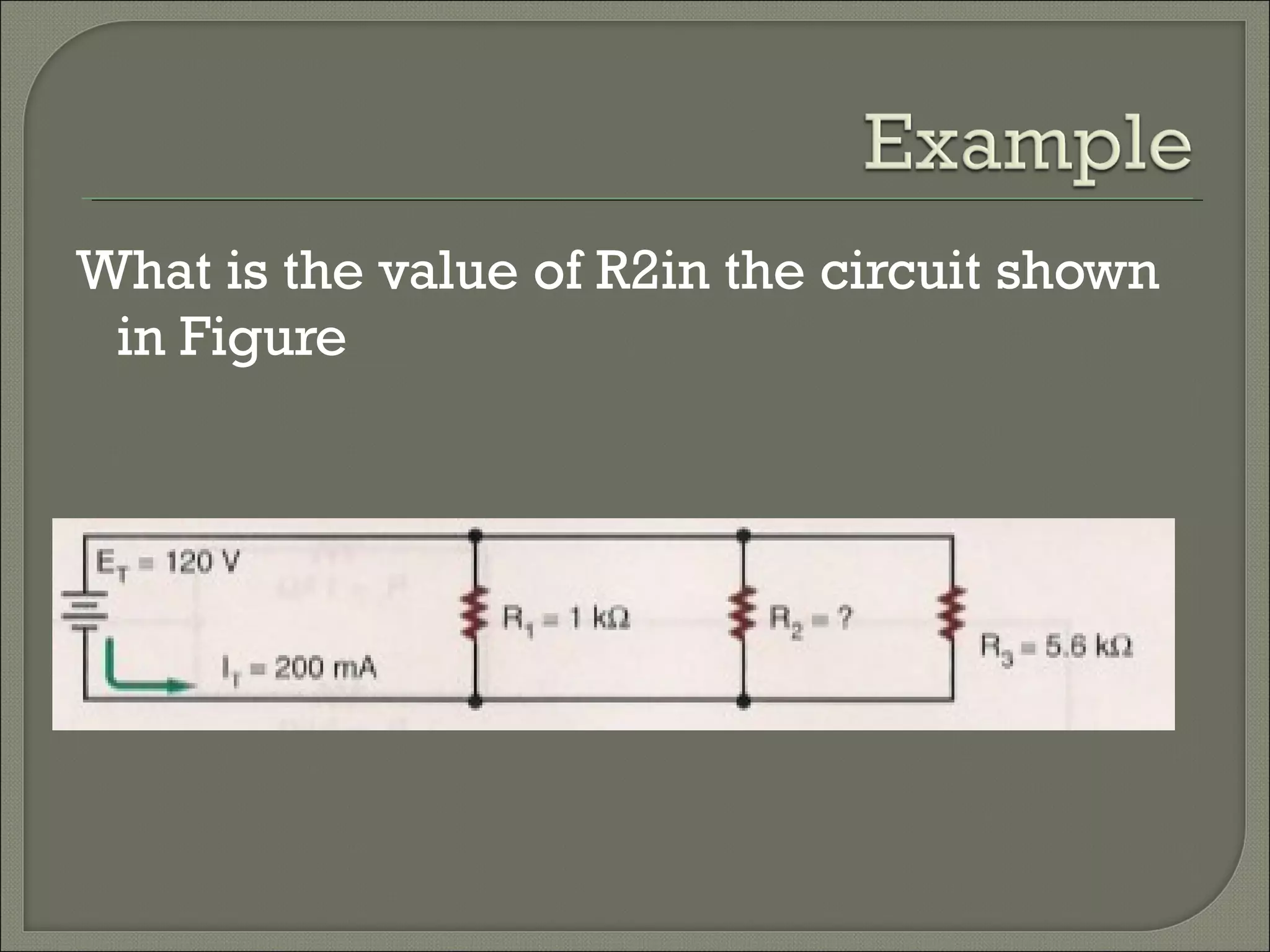
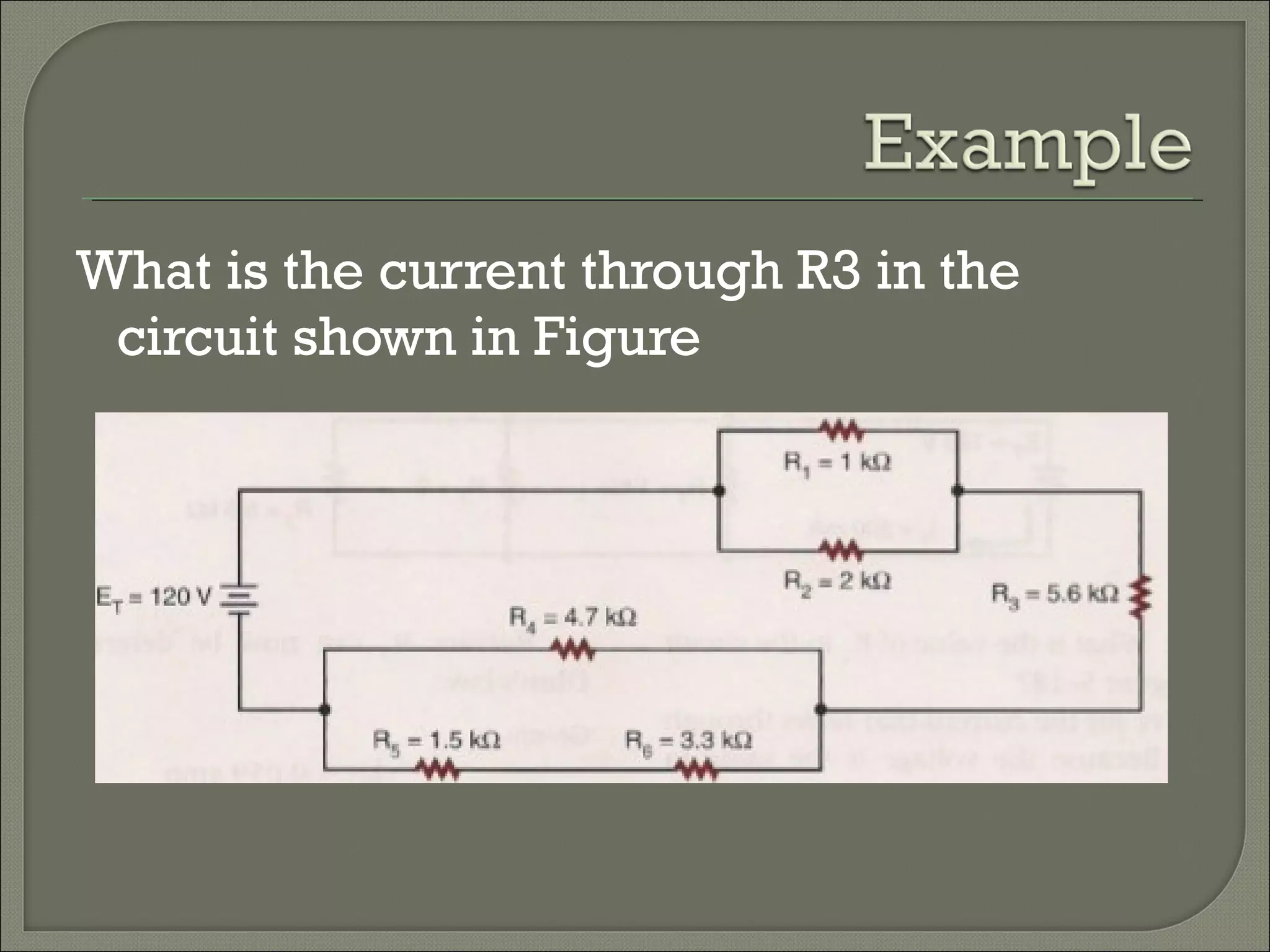
This document discusses Ohm's law and basic circuit concepts. It defines key terms like voltage, current, resistance, power, and energy. It explains that voltage is directly proportional to current based on Ohm's law. Circuits can be connected in series or parallel, and examples show how to calculate current, voltage, resistance, and power in different circuit configurations using Ohm's law.

1. Ohm’s Law & Circuits

2. 2
A. Voltage-electricalpotential;anelectricalpressurecreatedbythebuildupofcharge;causes
chargedparticlestomove
B. Volt-unitofvoltage;Symbol=V
C. Electromotiveforce-ahistoricaltermusedtodescribevoltage;Symbol=E
(Nolongerrelevant,thedefinitionofforceissomethingthatcausesamasstoaccelerate,andvoltageorEMFdoesnotfitthat
definition).Eisnowcommonlyusedasasymbolforelectricfieldstrength.
A. Current-theflowormovementofelectrons
B. Ampere-unitofcurrent;Symbol=I
C. Resistance-oppositiontocurrentflow

3. H. Energy- the fundamental ability to do work
I. Joule- unit of energy; Symbol= J
J. Electrical Power- the rate of electrical energy used in a
circuit; calculated by multiplying current times voltage,
or
P = V • I
K. Watt- unit of measurement for power; a watt is one
joule per second (J/s); Symbol= W
L. Ohm’s Law- a formula describing the mathematical
relationship between voltage, current, and resistance;
one of the most commonly used equations in all of
science
3

4. M. Directly proportional- having a constant ratio; a situation
where one variable moves in the same direction as another
variable when other conditions are constant
M. Inversely proportional- having a constant but inverse ratio;
a situation where one variable moves in the opposite
direction from another variable when other conditions
remain constant
4
• Example- current doubles when voltage is doubled if
resistance is held constant; thus, voltage and current are
directly proportional
• Example- with a constant voltage, current decreases when
resistance increases; thus, current and resistance are inversely
proportional

5. 5
• I – Electrical current in amperes
• R – Resistance in ohms
• V – Represents voltage in volts
• A – Represents amperes
• Ω – Represents ohms
• E – Electromotive force (emf) in volts,
sometimes used as an alternate
symbol for voltage

6.  Power is an indication of how much work
(the conversion of energy from one form
to another) can be done in a specific
amount of time; that is, a rate of doing
work.

7.  Power can be delivered or absorbed as
defined by the polarity of the voltage and the
direction of the current.
t
W
P =
second/joule1(W)Watt1 =

8.  Energy (W) lost or gained by any system
is determined by:
W = Pt
 Since power is measured in watts (or
joules per second) and time in seconds,
the unit of energy is the wattsecond (Ws)
or joule (J)

9.  The watt-second is too small a quantity for
most practical purposes, so the watt-hour
(Wh) and kilowatt-hour (kWh) are defined
as follows:
 The killowatt-hour meter is an instrument
used for measuring the energy supplied to
a residential or commercial user of
electricity.
1000
(h)time(W)power
(kWh)Energy
×
=
(h)time(W)power(Wh)Energy ×=

10.  Efficiency (η) of a system is determined
by the following equation:
η = Po / Pi
Where: η = efficiency (decimal number)
Po = power output
Pi = power input

11.  The basic components of a generating (voltage) system
are depicted below, each component has an associated
efficiency, resulting in a loss of power through each
stage.
Insert Fig 4.19Insert Fig 4.19

12. Insert Table 4.1Insert Table 4.1

13. Basic Laws of Circuits
Ohm’s Law:
The voltage across a resistor is directly proportional to the current
moving through the resistor.
+ _v ( t )i ( t )
R
v ( t ) = R i ( t )
+_ v ( t )i ( t )
R
v ( t ) = R i ( t )_
(2.1)
(2.2)

14. Basic Laws of Circuits
Ohm’s Law:
Directly proportional means a straight line relationship.
v(t)
i(t)
R
The resistor is a model and will not produce a straight line
for all conditions of operation.
v(t) = Ri(t)

15. Basic Laws of Circuits
Ohm’s Law: About Resistors:
The unit of resistance is ohms( Ω).
A mathematical expression for resistance is
l
R
A
ρ=
( )
2
: ( )
: ( )
:
l Thelengthof theconductor meters
A Thecross sectional area meters
Theresistivity mρ
−
Ω ⋅
(2.3)

16. Basic Laws of Circuits
Ohm’s Law: About Resistors:
We remember that resistance has units of ohms. The reciprocal of
resistance is conductance. At one time, conductance commonly had units
of mhos (resistance spelled backwards).
In recent years the units of conductance has been established as seimans (S).
Thus, we express the relationship between conductance and resistance as
1
G
R
= (2.4)
We will see later than when resistors are in parallel, it is convenient
to use Equation (2.4) to calculate the equivalent resistance.
(S)

17. Basic Laws of Circuits
Ohm’s Law: Ohm’s Law: Example 2.1.
Consider the following circuit.
+
_
1 1 5 V R M S
( a c )
R
( 1 0 0 W a t t lig h t b u lb )
V
Determine the resistance of the 100 Watt bulb.
2
2
2
2
115
132.25
100
V
P VI I R
R
V
R ohms
P
= = =
= = =
(2.5)
A suggested assignment is to measure the resistance of a 100 watt light
bulb with an ohmmeter. Debate the two answers.

18.  Resistivity is a material property
• Dependent on the number of free or mobile
charges (usually electrons) in the material.
 In a metal, this is the number of electrons from the
outer shell that are ionized and become part of the
‘sea of electrons’
• Dependent on the mobility of the charges
 Mobility is related to the velocity of the charges.
 It is a function of the material, the frequency and
magnitude of the voltage applied to make the charges
move, and temperature.

19. Material Resistivity (Ω-cm) Usage
Silver 1.64x10-8
Conductor
Copper 1.72x10-8
Conductor
Aluminum 2.8x10-8
Conductor
Gold 2.45x10-8
Conductor
Carbon (Graphite) 4x10-5
Conductor
Germanium 0.47 Semiconductor
Silicon 640 Semiconductor
Paper 1010
Insulator
Mica 5x1011
Insulator
Glass 1012
Insulator
Teflon 3x1012
Insulator

20. mA Milliamp = 0.001 amps
Kilo ohm = 1000 ohmsKΩ

21. Resistance takes into account the physical
dimensions of the material
where:
L is the length along which
the carriers are moving
A is the cross sectional area
that the free charges move
through.
A
L
R ρ=

22. Voltage drop across a resistor is
proportional to the current flowing
through the resistor
Units: V = AΩ
where A = C/s
iR=v

24. Insert Fig 4.8Insert Fig 4.8

25. If the resistor is a perfect
conductor (or a short
circuit)
R = 0 Ω,
then
v = iR = 0 V
no matter how much
current is flowing through
the resistor

26. If the resistor is a
perfect insulator, R = ∞
Ω
then
no matter how much
voltage is applied to
(or dropped across)
the resistor.
A

27.  Conductance is the reciprocal of
resistance
G = R-1
= i/v
Unit for conductance is S (siemens) or
(mhos)
G = Aσ/L
where σ is conductivity,
which is the inverse of resistivity, ρ

28. p = iv = i(iR) = i2
R
p = iv = (v/R)v = v2
/R
p = iv = i(i/G) = i2
/G
p = iv = (vG)v = v2
G

29.  Since R and G are always real positive
numbers
• Power dissipated by a resistor is always positive
 The power consumed by the resistor is
not linear with respect to either the
current flowing through the resistor or
the voltage dropped across the resistor
• This power is released as heat. Thus, resistors
get hot as they absorb power (or dissipate
power) from the circuit.

30.  There is no power dissipated in a short
circuit.
 There is no power dissipated in an open
circuit.
W0)0()V0(v 22
=Ω== Rpsc
W0)()A0(i 22
=Ω∞== Rpoc

31.  The path that the current follows is called
an electric circuit.
 All electric circuits consist of a voltage
source, a load, and a conductor
 The voltage source establishes a
difference of potential that forces the
current to flow.

32.  A series circuit offers a single path for
current flow.

33.  A parallel circuit offers more than one
path for current flow.

34.  A series-parallel circuit is a combination
of a series circuit and a parallel circuit.

35.  How much current flows in the circuit
shown in Figure 1?
Figure 1

36. Given:
IT= ?
ET = 12 volts
RT= 1000 ohms
IT = ET/ RT
IT = 12 /1000
IT = 0.012 amp or 12 milliamps

37.  In the circuit shown in Figure 2, how
much voltage is required to produce 20
milliamps of current flow
Figure 2

38. Given:
IT= 20 mA = = 0.02 amp
ET = ?
RT= 1.2 kΩ = ohms

39.  In the circuit shown in Figure 5-10, how
much voltage is required to produce 20
milliamps of current flow?

40. Solution:
IT = ET / RT
0.02 = ET / 1200
ET = 24 volts

41.  What resistance value is needed for the
circuit shown in Figure 5-11 to draw 2
amperes of current?

42. Given :
IT = 2 amps
ET = 120 volts
RT = ?
Solution:
IT = ET / RT
2 = 120 / RT
60 ohms = RT

43.  What is the total current flow in the
circuit?

44. Given:
IT= ?
ET = 12 volts
RT =?
R1= 560 ohms
R2 = 680 ohms
R3 = 1 kΩ= 1000 ohms
Solution:
First solve for the total resistance of the circuit:
RT = R1 + R2 + R3
RT = 560 + 680 + 1000 = 2240 ohms
RT= 2240 ohms

45. Draw an equivalent circuit. See Figure. Now
solve for the total current flow:
IT = ET / RT
IT = 12 / 2240
IT = 0.0054 amp or 5.4 milliamp

46. How much voltage is dropped across
resistor R2 in the circuit

47. Given:
IT =?
ET = 48 volts
RT =?
R1 = 1.2 k Ω = 1200 ohms
R2 = 3.9 k Ω = 3900 ohms
R3 = 5.6 k Ω = 5600 ohms
Solution:
First solve for the total circuit resistance:
RT = R1 + R2 + R3 = 1200 + 3900 + 5600
RT= 10,700 ohms
Draw the equivalent circuit. See Figure. Solve for the total current in the circuit:
IT = ET / RT
IT = 48 / 10,700
I = 0.0045 amp or 4.5 milliamps

48. Remember, in a series circuit, the same
current flows throughout the circuit.
Therefore, IR = IT
IR2 = ER2 / R2
0.0045 = ER / 3900
ER2 = 17.55 volts

49. What is the value of R2in the circuit shown
in Figure

50.  What is the value of R2 in the circuit
shown in Figure?
 First solve for the current that flows
through R1 and R3. Because the voltage is
the same in each branch of a parallel
circuit, each branch voltage is equal to
the source voltage of 120 volts.

51. Given:
IR1
ER1 = 120 volts
R1 = 1000 ohms
Solution:
IR1 = ER1 / R1
IR1 = 120 / 1000
IR1 = 0.12 amp
Given:
IR3
ER3 = 120 volts
R3 = 5600 ohms
Solution:
IR3 = ER3 / R3
IR3 = 120 / 5600

52. Circuit, the total current is equal to the sum of
the currents in the branch currents.
Given:
IT = 0.200 amp
IR1= 0.120 amp
IR2=?
IR3= 0.021 amp
Solution:
IT = IR1 + IR2+ IR3
0.200 = 0.120 + IR2 + 0.021
0.200 = 0.141 + IR2
0.200 - 0.141 = IR2

53. Resistor R2 can now be determined using
Ohm's law.
Given:
IR2 = 0.059 amp
ER2 = 120 volts
R2 = ?
IR2 = ER2 / R2
.
Solution:
0.059 = 120 / R2
R2 = 2033.9 ohms

54. What is the current through R3 in the
circuit shown in Figure

55. First determine the equivalent resistance
(RA) for resistors R1 and R2.
Given:
RA =?
R1 = 1000 ohms
R2 = 2000 ohms
Solution:
1 / RA= 1/R1 + 1/R2(adding fractions requires a common denominator)
1 / RA= 1/1000 + 1/2000
1 /RA = 666.67 ohms

56. Then determine the equivalent resistance (RB)
for resistors R4, R5, and R6• First, find the total
series resistance (Rs) for resistors R5 and R6.
Given:
Rs =?
R5 = 1500 ohms
R6= 3300 ohms
Solution:
Rs = R5 + R6
Rs = 1500 + 3300
Rs = 4800 ohms

57. Given:
RB =?
R4 = 4700 ohms
Rs = 4800 ohms
Solution:
1 / RB= 1/R4 + 1/Rs
1 / RB= 1/4700 + 1/4800
RB = 2375.30 ohms

58. Redraw the equivalent circuit substituting
RA and RB , and find the total series
resistance of the equivalent circuit. See
Figure
Given:
RT=?
RA = 666.67 ohms
R3 = 5600 ohms
RB = 2375.30 ohms

59. Solution:
RT= RA + R3 + RB
RT = 666.67 + 5600 + 2375.30
RT = 8641.97 ohms
Now solve for the total current through the equivalent circuit
using Ohm's law.
Given:
IT =?
ET = 120 volts
RT = 8641.97 ohms
Solution:
IT = ET / RT
IT = 120 / 8641.97
IT = 0.0139 amp or 13.9 milliamps

60. In a series circuit, the same current flows
throughout the circuit.Therefore, the
current flowing through R3 is equal to the
total current in the circuit.
IR3 = IT
IR3 =13.9 milliamps