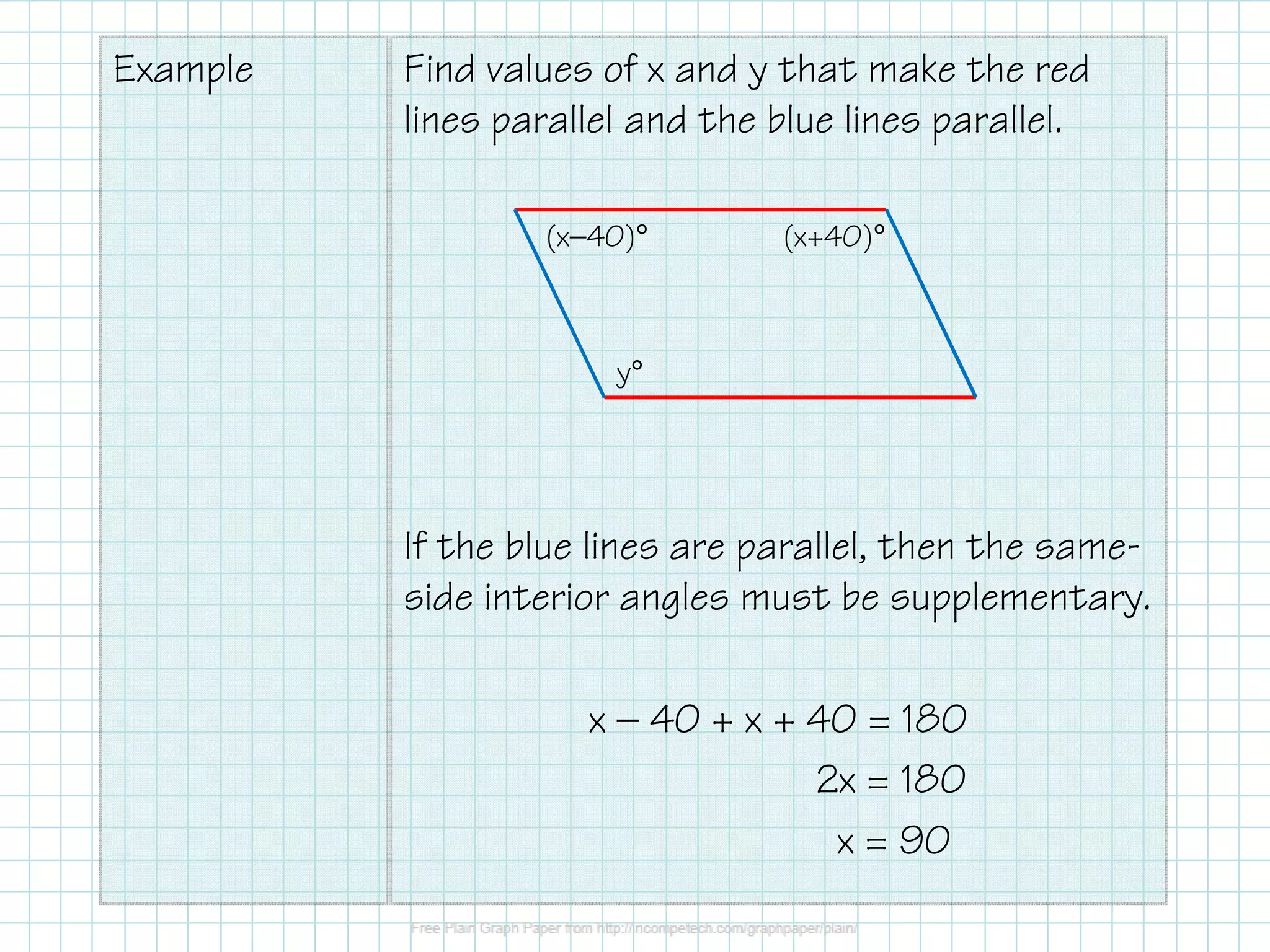
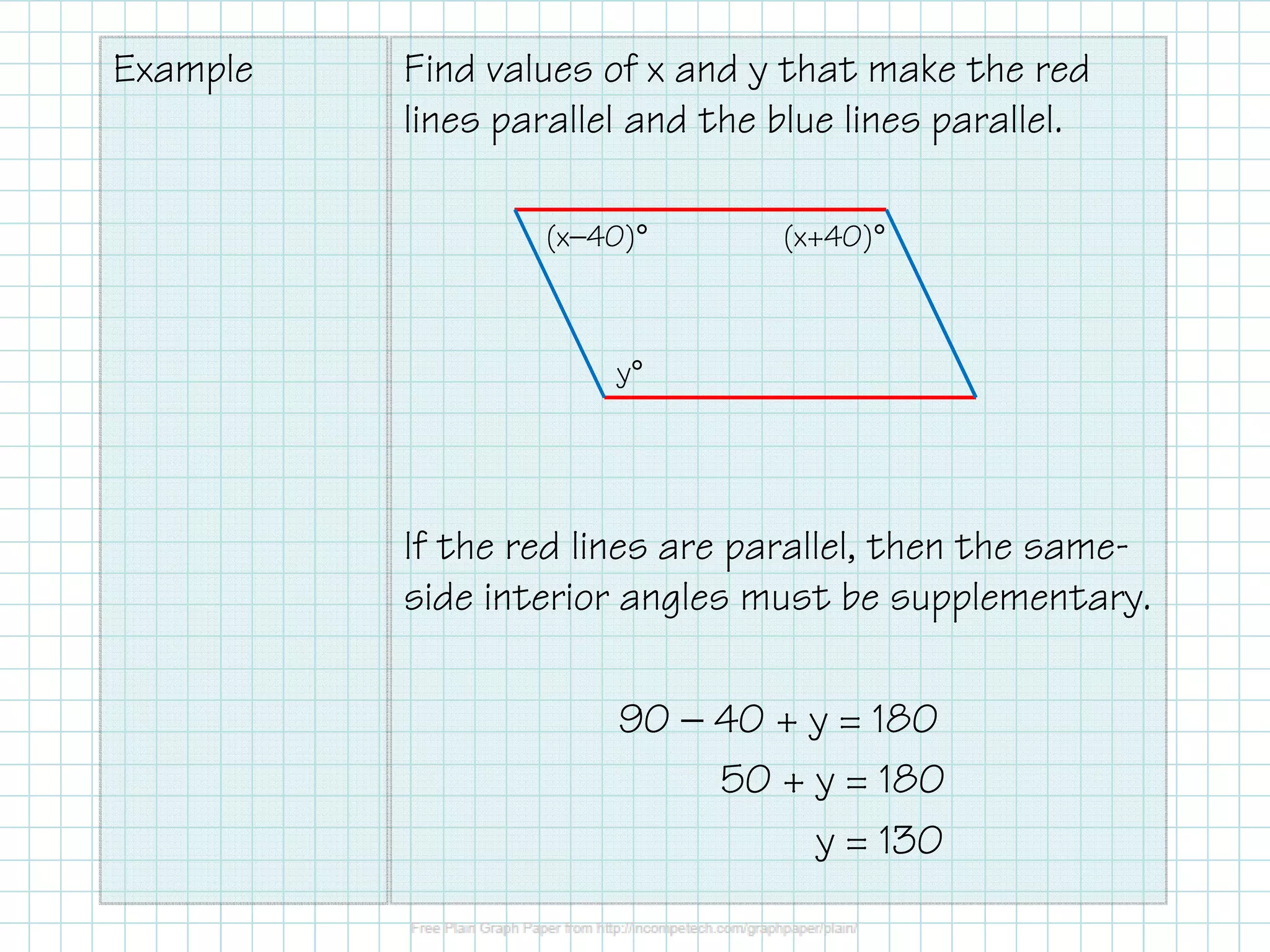
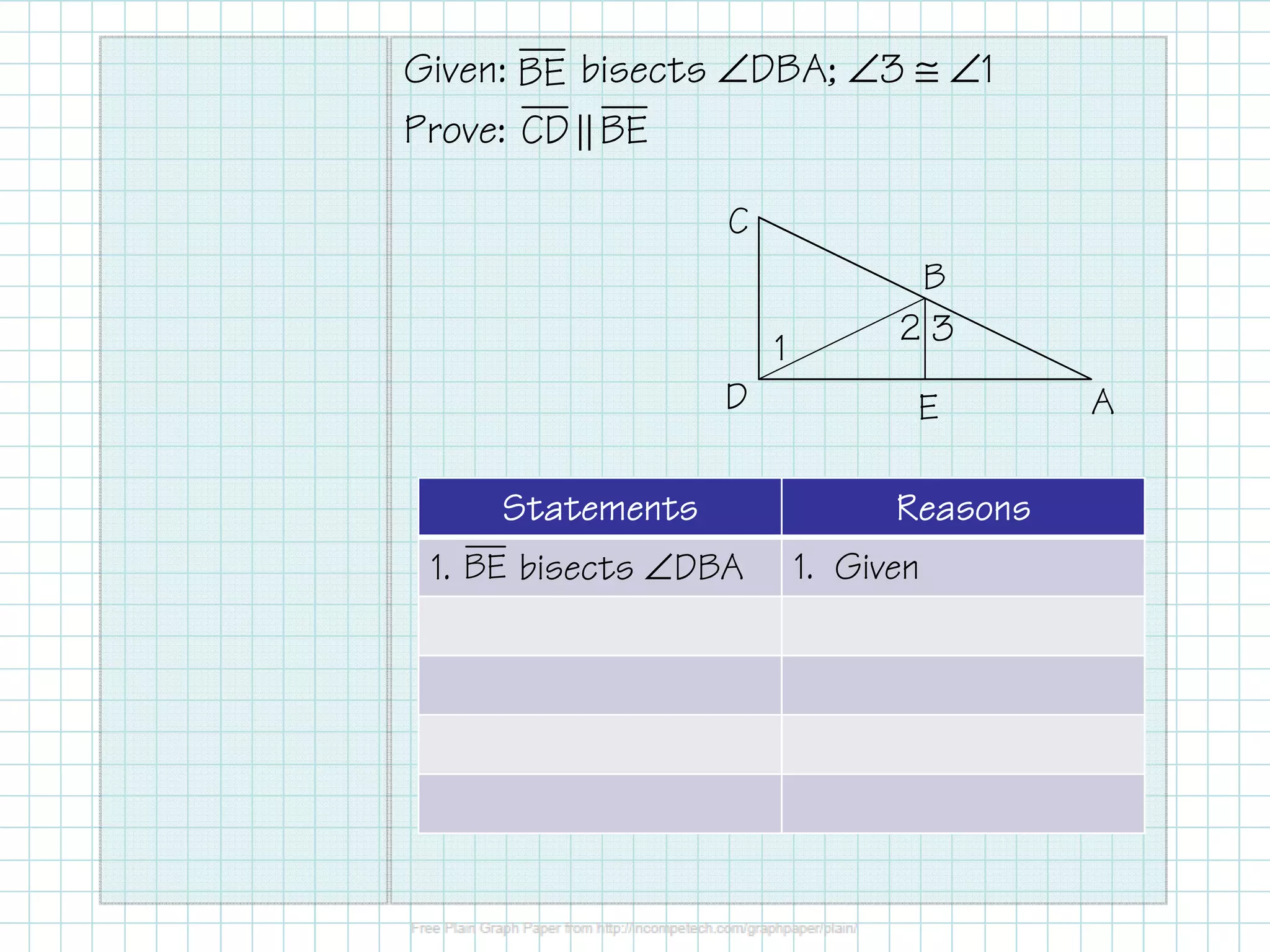
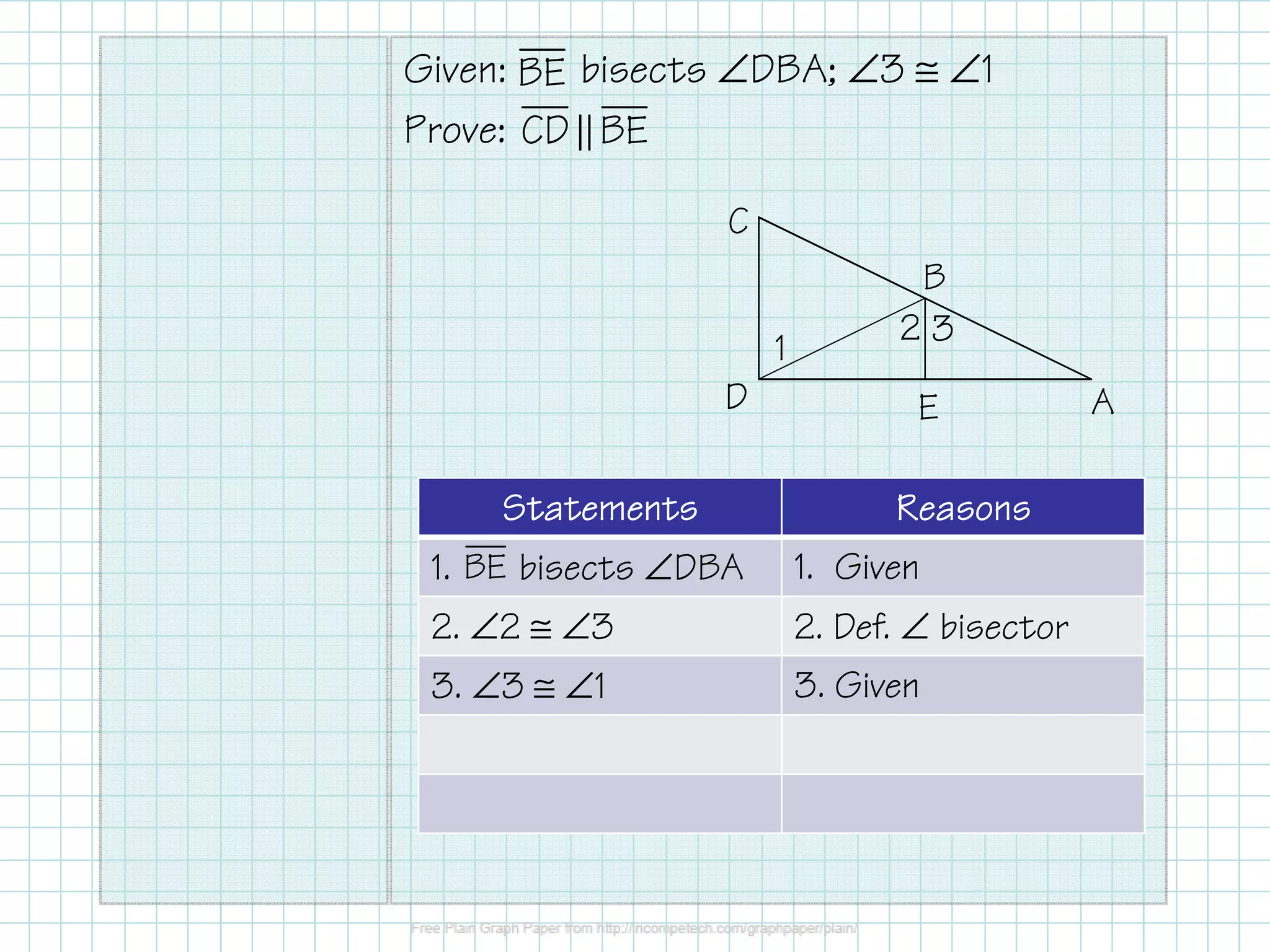
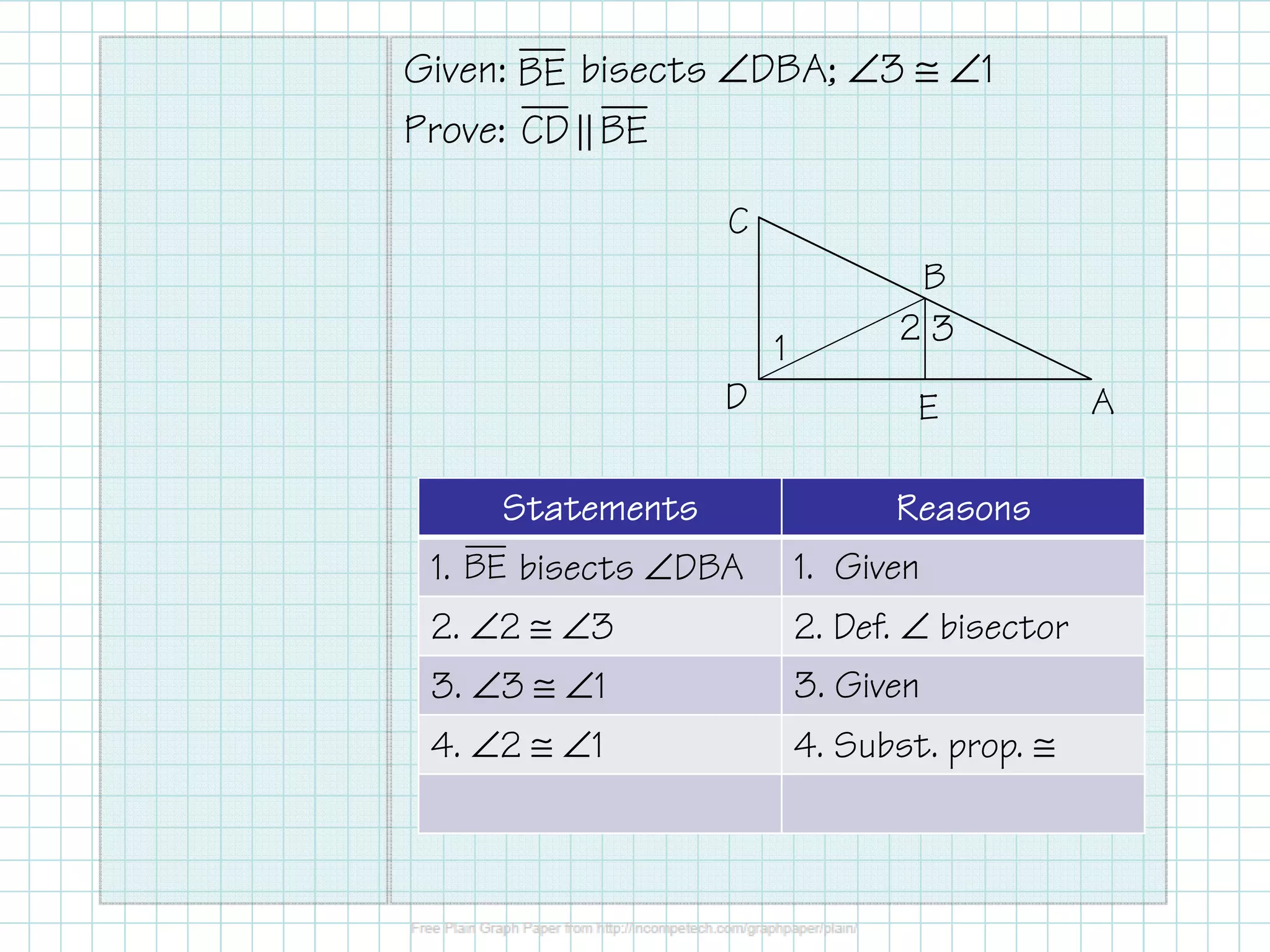
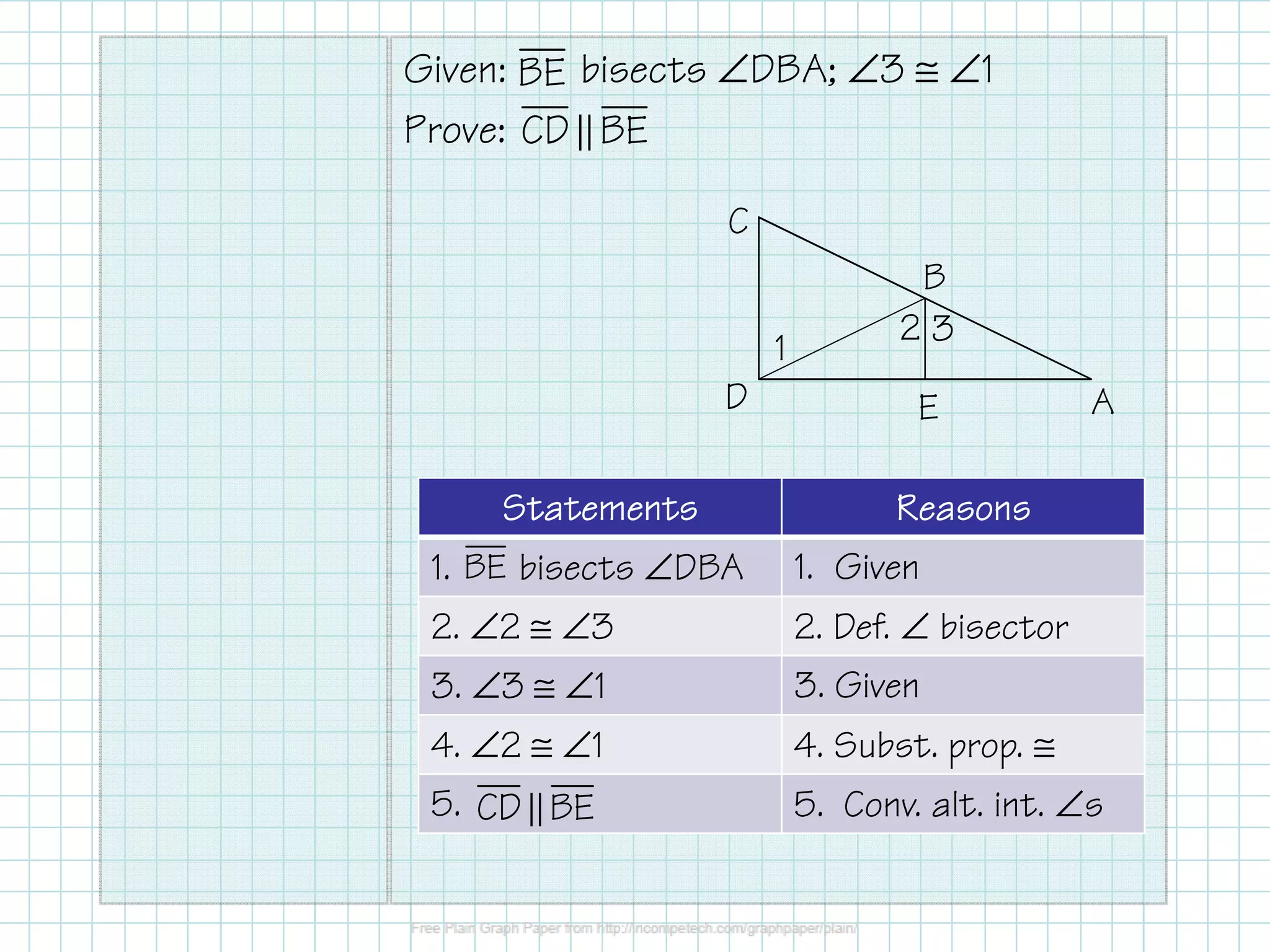
1. The document discusses using angles formed by a transversal to show that lines are parallel using the parallel line theorems. 2. It provides an example of finding values of x and y that make two sets of lines parallel using the same-side interior angle theorem. 3. It also shows a proof that lines CD and BE are parallel given that angle BE bisects angle DBA and angle 3 is congruent to angle 1 using alternate interior angles.

1. Obj. 12 Proving Lines Parallel
The student is able to (I can):
• Use angles formed by a transversal to show that lines are
parallel.

2. Recall that the converse of a theorem is
found by exchanging the hypothesis and
conclusion.
The converses of the parallel line theorems
can be used to prove lines parallel
• Corresponding Angles
• Alternate Interior Angles
• Alternate Exterior Angles
— If angles are congruent, then the lines
are parallel.
• Same-Side Interior Angles
— If angles are supplementary, then the
lines are parallel.

3. Example Find values of x and y that make the red
lines parallel and the blue lines parallel.
(x−40)° (x+40)°
If the blue lines are parallel, then the same-side
interior angles must be supplementary.
x − 40 + x + 40 = 180
2x = 180
x = 90
y°

4. Example Find values of x and y that make the red
lines parallel and the blue lines parallel.
(x−40)° (x+40)°
If the red lines are parallel, then the same-side
interior angles must be supplementary.
90 − 40 + y = 180
50 + y = 180
y = 130
y°

5. Given: bisects ÐDBA; Ð3 @ Ð1
Prove:
BE
CD BE
C
B
2 3
1
D E A
Plan of proof: Because bisects ÐDBA,
BE
Ð2 @ Ð3. Because Ð3 @ Ð1,
I can set Ð2 @Ð1 using
substitution. Ð1 and Ð2 are
alternate interior angles, and
since they are congruent, the
lines are parallel.

6. Given: bisects ÐDBA; Ð3 @ Ð1
Prove:
BE
CD BE
C
B
2 3
1
D E A
SSSSttttaaaatttteeeemmmmeeeennnnttttssss RRRReeeeaaaassssoooonnnnssss
1. B E bisects ÐDBA 1. Given

7. Given: bisects ÐDBA; Ð3 @ Ð1
Prove:
BE
CD BE
C
B
2 3
1
D E A
SSSSttttaaaatttteeeemmmmeeeennnnttttssss RRRReeeeaaaassssoooonnnnssss
1. BE
bisects ÐDBA 1. Given
2. Ð2 @ Ð3 2. Def. Ð bisector

8. Given: bisects ÐDBA; Ð3 @ Ð1
Prove:
BE
CD BE
C
B
2 3
1
D E A
SSSSttttaaaatttteeeemmmmeeeennnnttttssss RRRReeeeaaaassssoooonnnnssss
1. BE
bisects ÐDBA 1. Given
2. Ð2 @ Ð3 2. Def. Ð bisector
3. Ð3 @ Ð1 3. Given

9. Given: bisects ÐDBA; Ð3 @ Ð1
Prove:
BE
CD BE
C
B
2 3
1
D E A
SSSSttttaaaatttteeeemmmmeeeennnnttttssss RRRReeeeaaaassssoooonnnnssss
1. BE
bisects ÐDBA 1. Given
2. Ð2 @ Ð3 2. Def. Ð bisector
3. Ð3 @ Ð1 3. Given
4. Ð2 @ Ð1 4. Subst. prop. @

10. Given: bisects ÐDBA; Ð3 @ Ð1
Prove:
BE
CD BE
C
B
2 3
1
D E A
SSSSttttaaaatttteeeemmmmeeeennnnttttssss RRRReeeeaaaassssoooonnnnssss
1. BE
bisects ÐDBA 1. Given
2. Ð2 @ Ð3 2. Def. Ð bisector
3. Ð3 @ Ð1 3. Given
4. Ð2 @ Ð1 4. Subst. prop. @
5. 5. Conv. alt. int. Ðs
CD BE