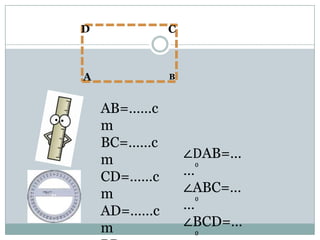
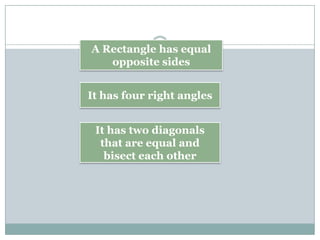
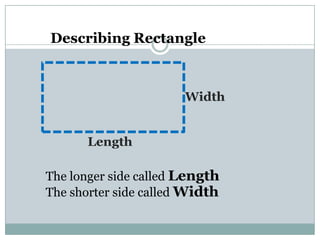
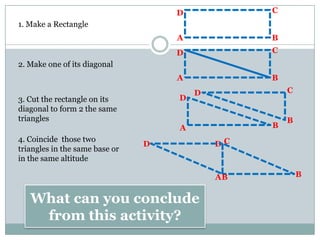
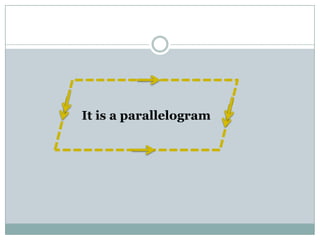
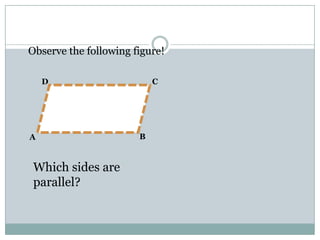
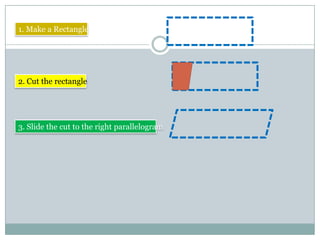
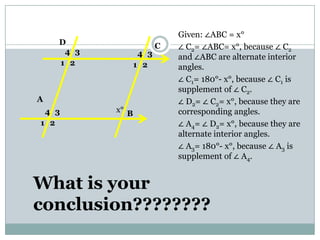
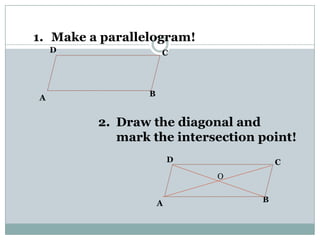
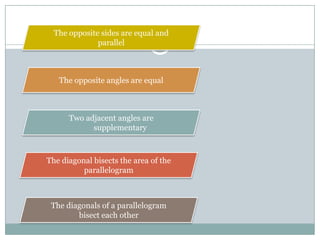
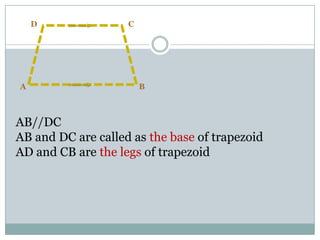
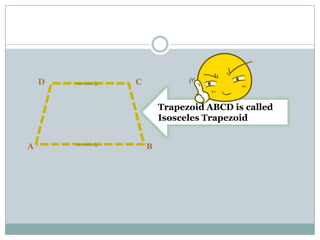
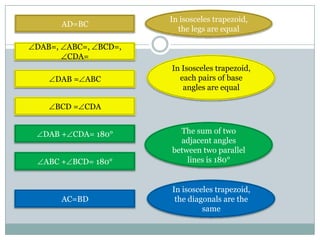
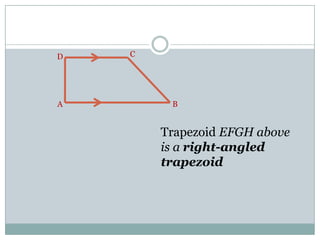
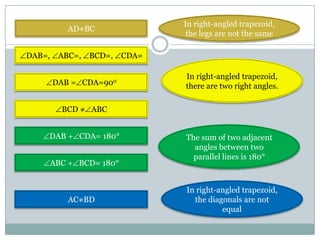
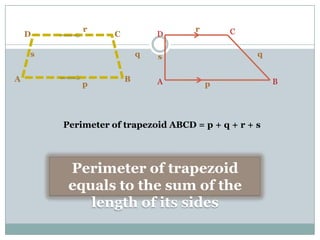
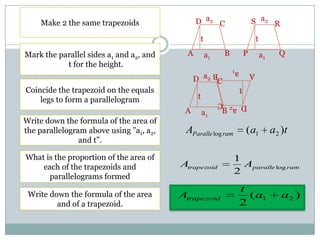
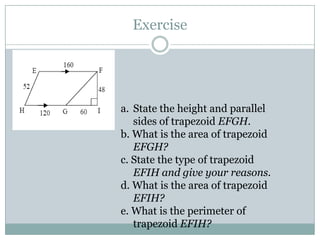
This document defines and describes properties of various quadrilaterals: - Rectangles have four right angles and opposite sides of equal length. The area formula is length x width. - Parallelograms have two pairs of parallel sides. The opposite angles are equal and adjacent angles sum to 180 degrees. Diagonals bisect each other. - Trapezoids have one pair of parallel sides. Isosceles trapezoids have two pairs of equal angles and equal or equal length diagonals. Right trapezoids contain one right angle. The area of any trapezoid is half the product of the height and sum of the parallel sides.

1. Q
U
A
D
R
I
L
A
T
E
R
A
L

2. Learning
Objectives
1. Define square, rectangular,
rhombus, kite, parallelogram, and
trapezoid
2. Describe the properties of square,
rectangular, rhombus, kite,
parallelogram, and trapezoid
3. Discover the formula of the
perimeter and area of square,
rectangular, rhombus, kite,
parallelogram, and trapezoid

3. Rectangles

4. a c t i iv t y 1

5. D C
BA
AB=……c
m
BC=……c
m
CD=……c
m
AD=……c
m
∠DAB=…
…⁰
∠ABC=…
…⁰
∠BCD=…
⁰

6. It has two diagonals
that are equal and
bisect each other
It has four right angles
A Rectangle has equal
opposite sides

7. Definition

8. A rectangle is a quadrilateral
that has 4 right angles and its
opposite sides are equal in
length.
Based on the properties
above, we can conclude
that:

9. Length
Width
Describing Rectangle
The longer side called Length
The shorter side called Width

10. Formula of The
Area

11. Suppose you have a room. The room
floor is in a rectangular shape. The
floor will be covered with square tiles.

13. It is a parallelogram

14. Parallelogram is a
quadrilateral whose opposite
sides are parallel.
What is parallelogram?

15. B
D C
A
Observe the following figure!
Which sides are
parallel?

16. a c t i iv t y 5

17. 1. Make a Rectangle
2. Cut the rectangle
3. Slide the cut to the right parallelogram

18. 1. Make a Rectangle
2. Make one of its diagonal
3. Cut the rectangle on its
diagonal to form 2 the same
triangles
4. Coincide those two
triangles in the same base or
in the same altitude
A
D C
B
A
D C
B
D
B
C
A B
D
A B
DD
B
C
What can you conclude
from this activity?

19. Let ABCD be a parallelogram and ∠ABC
= x°, find the other angles!
Use the properties of parallel lines!
B
D
C
A
Observe the figure below!

20. Given: ∠ABC = x°
∠ C2= ∠ABC= x°, because ∠ C2
and ∠ABC are alternate interior
angles.
∠ C1= 180°- x°, because ∠ C1 is
supplement of ∠ C2.
∠ D2= ∠ C2= x°, because they are
corresponding angles.
∠ A4= ∠ D2= x°, because they are
alternate interior angles.
∠ A3= 180°- x°, because ∠ A3 is
supplement of ∠ A4.
B
D
A
C
x°
1 2
34
1 2
34
1 2
34
What is your
conclusion????????

21. a c t i iv t y 6

22. B
D C
A
B
D C
A
O
1. Make a parallelogram!
2. Draw the diagonal and
mark the intersection point!

23. 3. Measure the length of the diagonal and the length
of line segment from the intersection point to each
vertices!
AC=… OA=… OB=…
BD=… OC=… OD=…
WHAT CAN YOU CONCLUDE FROM
THIS ACTIVITY?

24. 4. Cut the parallelogram on one of its diagonal!
5. Compare the area of the two parts!
6. Make another parallelogram which is the same as
the first parallelogram!
7. Repeat the step number 4 and 5 but on another
diagonal!
What can you conclude?

25. The Properties

26. The opposite sides are equal and
parallel
The opposite angles are equal
Two adjacent angles are
supplementary
The diagonal bisects the area of the
parallelogram
The diagonals of a parallelogram
bisect each other

27. Trapezoid

28. D
i
nf
e
i
i
ot
n

29. Trapezoid is a
quadrilateral with one pair
of exactly parallel sides

30. D C
A B
AB//DC
AB and DC are called as the base of trapezoid
AD and CB are the legs of trapezoid

31. T
p
ea
r
i
z
do
K i n sd
o f

32. I
S
O L
E
SC
S E
r a p dozt e i

33. D C
A B
Trapezoid ABCD is called
Isosceles Trapezoid

34. a c t i iv t y 7

35. 1. Measure the length of side AD and BC
2. Measure DAB, ABC, BCD, CDA
3. Measure the length of AC and BD
4. What is the relation between DAB and ABC?
5. What is the relation between BCD and CDA?
6. What is the relation between DAB and CDA?
7. What is the relation between ABC and BCD?
8. What is the relation of AC and BD?

36. DAB=, ABC=, BCD=,
CDA=
DAB = ABC
BCD = CDA
DAB + CDA= 180°
ABC + BCD= 180°
AD=BC
AC=BD
In isosceles trapezoid,
the legs are equal
In Isosceles trapezoid,
each pairs of base
angles are equal
The sum of two
adjacent angles
between two parallel
lines is 180°
In isosceles trapezoid,
the diagonals are the
same

37. r a p dozt e i
R
I
G A
N
GT
H - L E
D

38. CD
BA
Trapezoid EFGH above
is a right-angled
trapezoid

39. a c t i iv t y 8

40. 1. Measure the length of side AD and BC
2. Measure DAB, ABC, BCD, CDA
3. Measure the length of AC and BD
4. What is the relation between DAB and ABC?
5. What is the relation between BCD and CDA?
6. What is the relation between DAB and CDA?
7. What is the relation between ABC and BCD?
8. What is the relation of AC and BD?

41. DAB=, ABC=, BCD=, CDA=
DAB = CDA=900
BCD ≠ ABC
DAB + CDA= 180°
ABC + BCD= 180°
AD≠BC
AC≠BD
In right-angled trapezoid,
the legs are not the same
In right-angled trapezoid,
there are two right angles.
The sum of two adjacent
angles between two
parallel lines is 180°
In right-angled trapezoid,
the diagonals are not
equal

42. Perimeter of
Trapezoid

43. D C
A B
s
r
q
p
CD
BA
s
r
q
p
Perimeter of trapezoid ABCD = p + q + r + s
Perimeter of trapezoid
equals to the sum of the
length of its sides

44. Formula
of The
Area

45. I
n
v
e
t
n
i o
n

46. S R
P Qa1
a2
t
D C
A Ba1
a2
t
D C
A Ba1
a2
t
DC
AB a1
a2
t
taaA ramParalle )( 21log
ramparalletrapezoid AA log
2
1
)(
2
21 aa
t
Atrapezoid
Make 2 the same trapezoids
Mark the parallel sides a1 and a2, and
t for the height.
Coincide the trapezoid on the equals
legs to form a parallelogram
Write down the formula of the area of
the parallelogram above using ”a1, a2,
and t”.
What is the proportion of the area of
each of the trapezoids and
parallelograms formed
Write down the formula of the area
and of a trapezoid.

47. The area of a
trapezoid is half of
the product of its
height and the sum of
the parallel sides.

48. Exercise
a. State the height and parallel
sides of trapezoid EFGH.
b. What is the area of trapezoid
EFGH?
c. State the type of trapezoid
EFIH and give your reasons.
d. What is the area of trapezoid
EFIH?
e. What is the perimeter of
trapezoid EFIH?