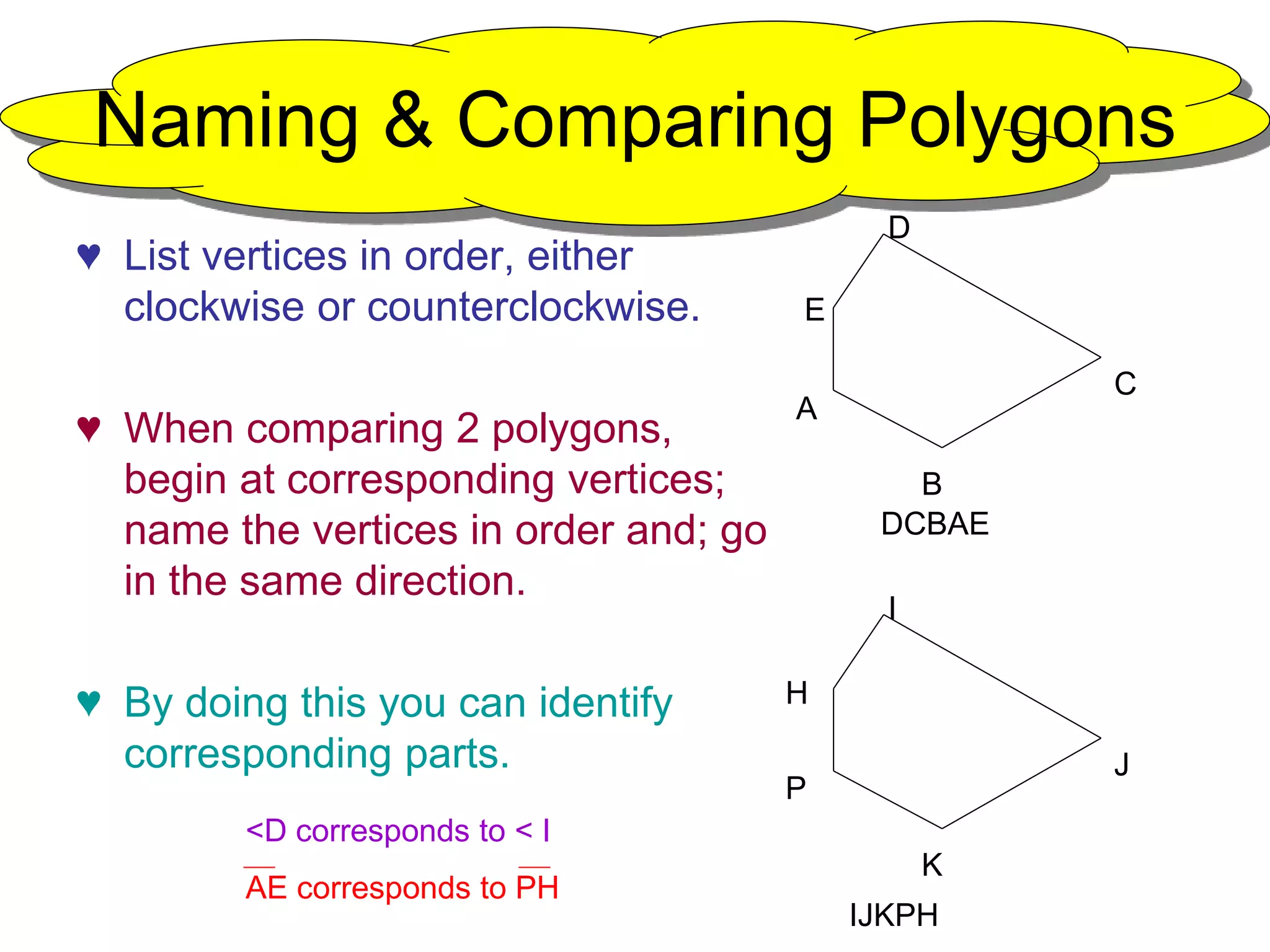
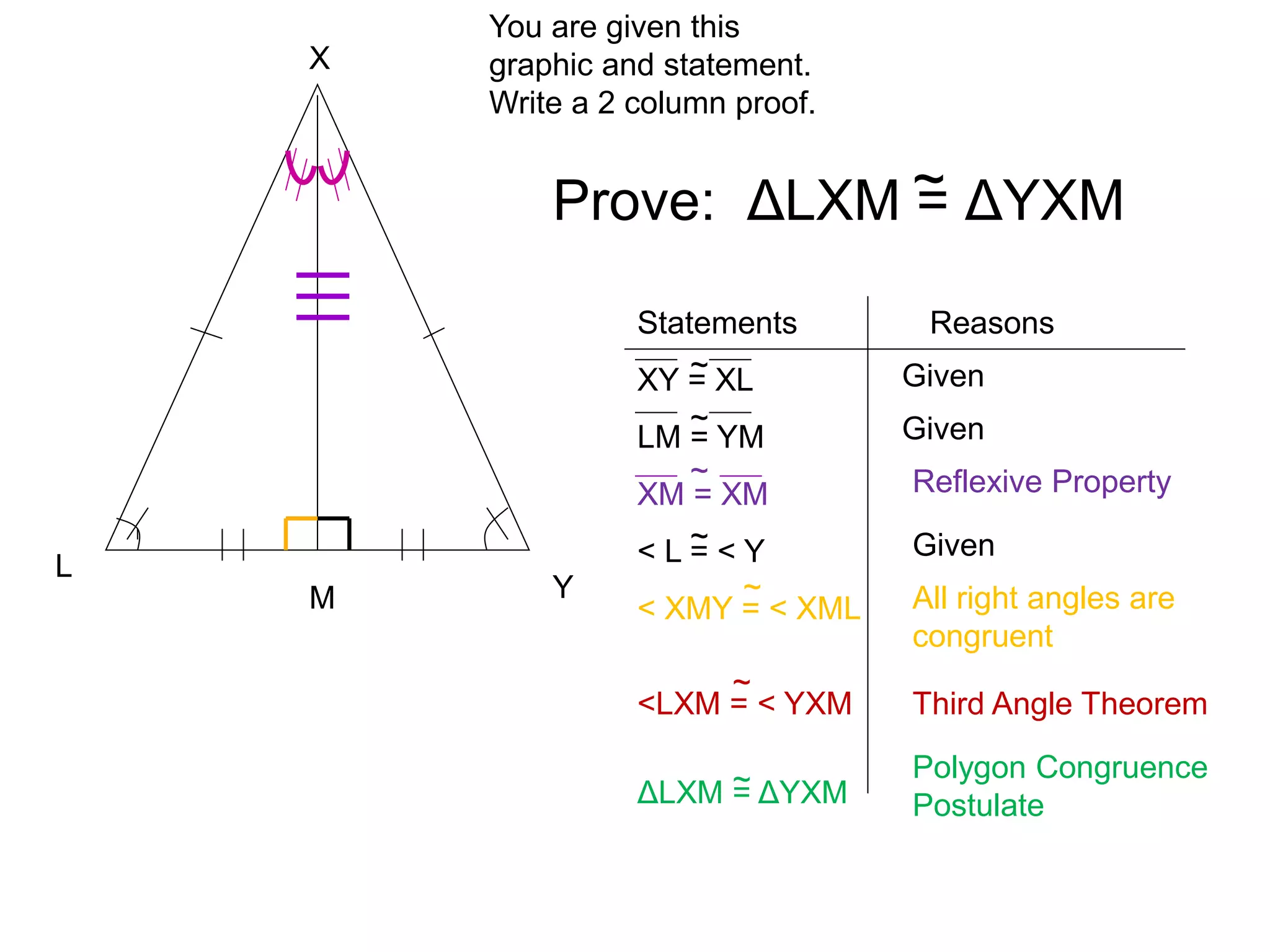
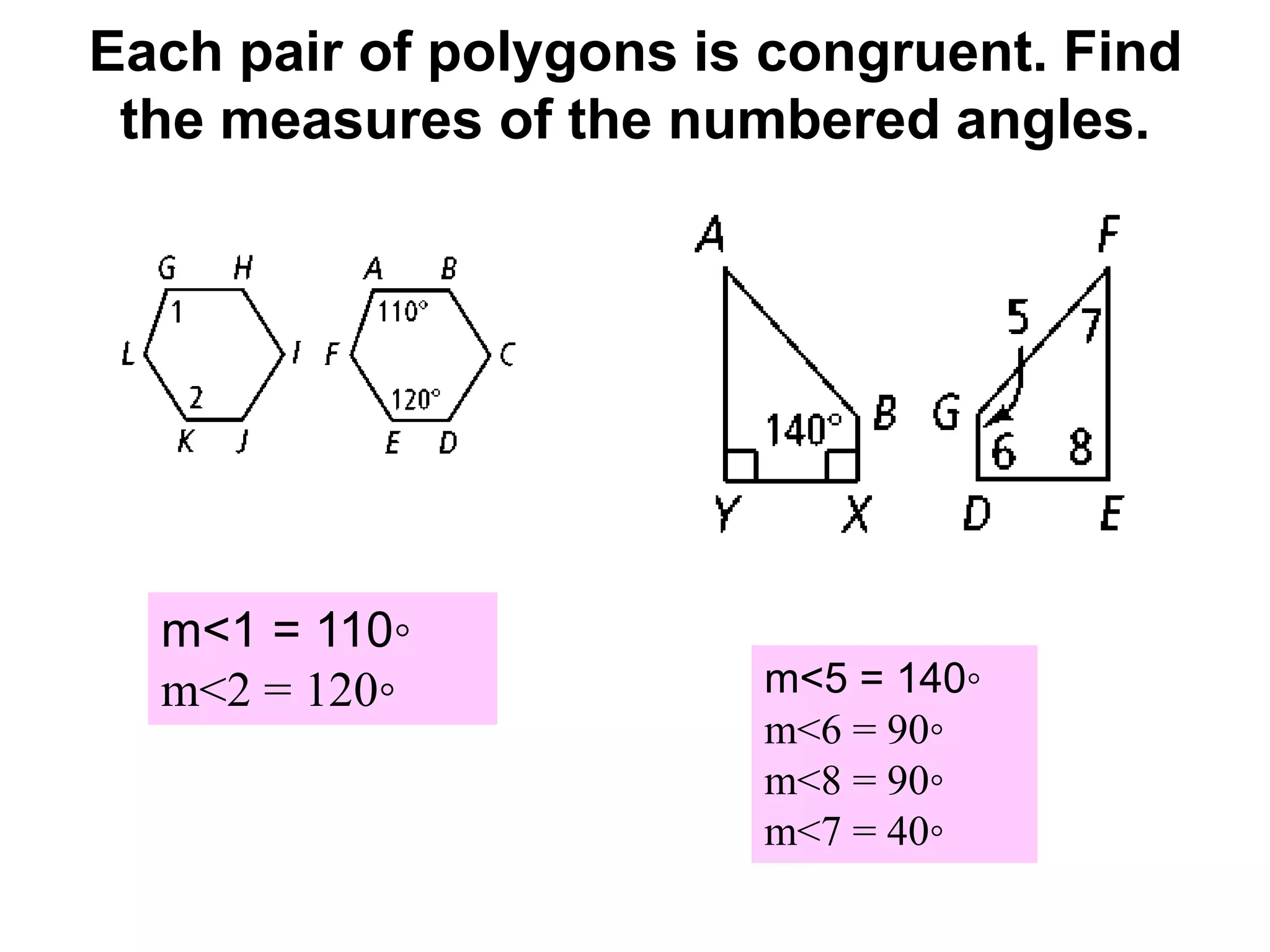
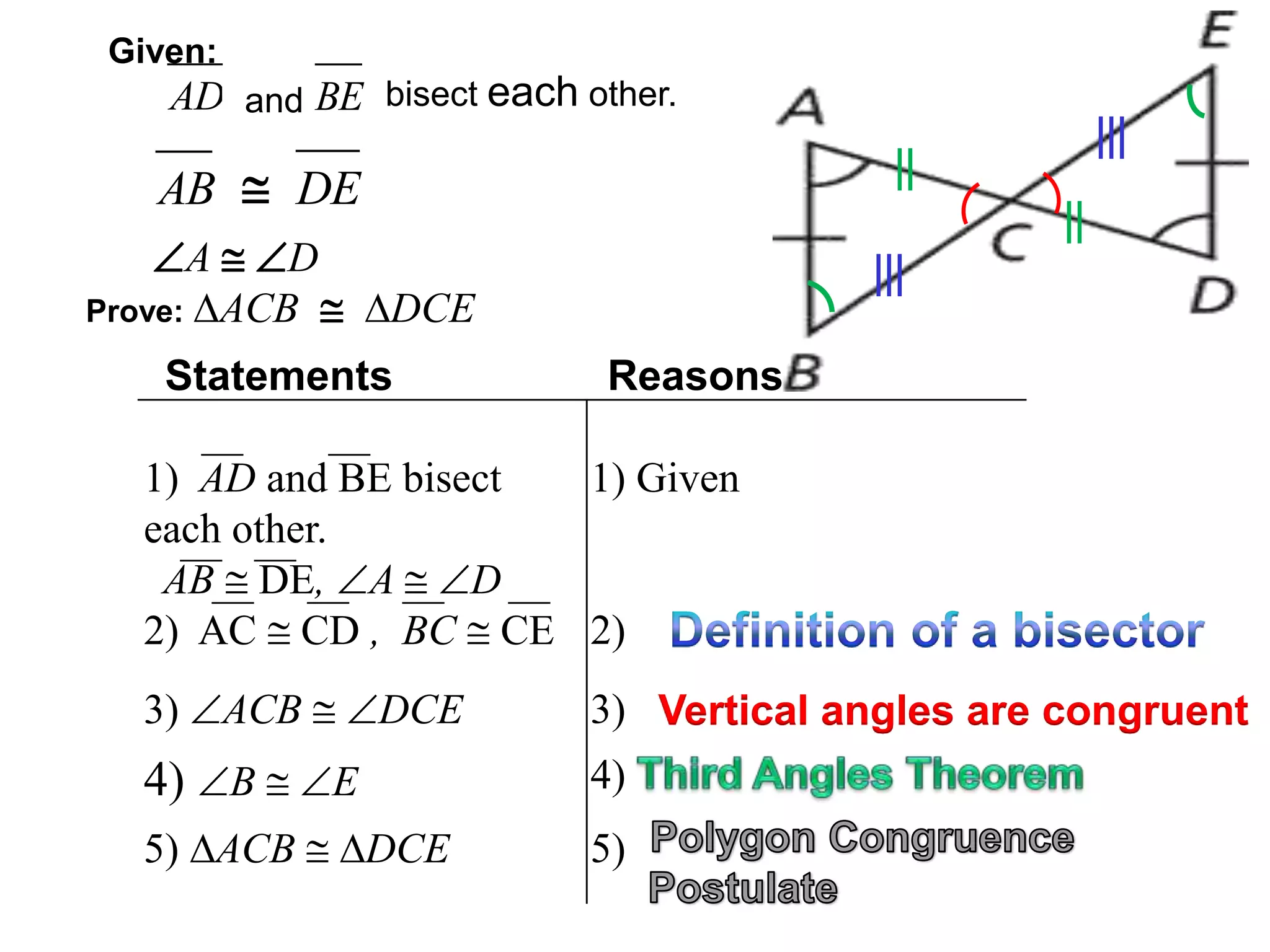
This document provides information about naming and comparing polygons, identifying corresponding parts of polygons, and determining if polygons are congruent. It defines what makes polygons congruent as having corresponding angles and sides that are congruent. It also introduces the Polygon Congruence Postulate and Third Angle Theorem, which can be used to prove polygons or triangles are congruent.

1. 4.1 Congruent
Polygons

2. Naming & Comparing Polygons
♥ List vertices in order, either
clockwise or counterclockwise.
♥ When comparing 2 polygons,
begin at corresponding vertices;
name the vertices in order and; go
in the same direction.
♥ By doing this you can identify
corresponding parts.
A
D
C
B
E
DCBAE
P
I
J
K
H
IJKPH
<D corresponds to < I
AE corresponds to PH

3. Name corresponding parts
• Name all the angles that correspond:
A
D
C
B
E
P
I
J
K
H
< D corresponds to < I
< C corresponds to < J
< B corresponds to < K
< A corresponds to < P
< E corresponds to < H
DCBAE IJKPH
• Name all the segments that correspond:
DC corresponds to IJ
CB corresponds to JK
BA corresponds to KP
AE corresponds to PH
ED corresponds to HI
How many
corresponding
angles are
there?
How many
corresponding
sides are there?
5 5

4. • How many ways
can you name
pentagon DCBAE?A
D
C
B
E
10
Do it.
DCBAE
CBAED
BAEDC
AEDCB
EDCBA
Pick a vertex and go clockwise Pick a vertex and go counterclockwise
DEABC
CDEAB
BCDEA
ABCDE
EABCD

5. Polygon Congruence
Postulate
If each pair of corresponding angles is
congruent, and each pair of corresponding
sides is congruent, then the two polygons
are congruent.

6. Congruence Statements
• Given: These polygons
are congruent.
• Remember, if they are
congruent, they are
EXACTLY the same.
• That means that all of the
corresponding angles are
congruent and all of the
corresponding sides are
congruent.
• DO NOT say that ‘all
the sides are congruent”
and “all the angles are
congruent”, because they
are not.
G
H
FE
C
D
B
A
ABCD = EFGH~

7. Third Angles Theorem
If two angles of one triangle are congruent
to two angles of another triangle, then the
third angles are congruent
A X
B
C
Y Z
If
<A = <X
and
<B = <Y,
then
<C = <Z

8. Statements Reasons
XY = XL
LM = YM
XM = XM
< L = < Y
< XMY = < XML
<LXM = < YXM
ΔLXM = ΔYXM
Prove: ΔLXM = ΔYXM~
X
YM
L
~
~
~
~
~
~
~
You are given this
graphic and statement.
Write a 2 column proof.
Given
Given
Reflexive Property
Third Angle Theorem
Given
All right angles are
congruent
Polygon Congruence
Postulate

9. Each pair of polygons is congruent. Find
the measures of the numbered angles.
m<1 = 110◦
m<2 = 120◦ m<5 = 140◦
m<6 = 90◦
m<8 = 90◦
m<7 = 40◦

10. A student says she can use the information in
the figure to prove ACB  ACD.
Is she correct? Explain.

11. 
bisect each other.
Statements Reasons
1) AD and BE bisect
each other.
AB  DE, A  D
1) Given
2) AC  CD , BC  CE 2)
3) ACB  DCE 3)
4) B  E 4)
5) ACB  DCE 5)
AD
AB DE
Given:
and
A  D
Prove: ACB  DCE
Vertical angles are congruent
BE

12. Assignment
4.1 Reteach
Worksheet
4.1 Practice
Worksheet