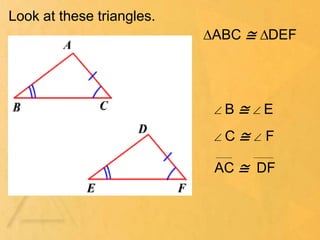
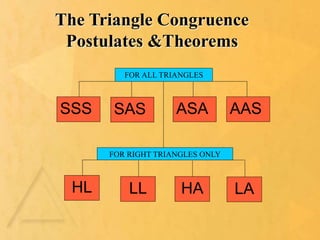
1. Triangles are congruent if all corresponding sides and angles are congruent. They will have the same shape and size but may be mirror images. 2. There are four main postulates and theorems used to prove triangles congruent: SSS (three sides), SAS (two sides and included angle), ASA (two angles and included side), and AAS (two angles and non-included side). 3. Corresponding parts of congruent triangles are also congruent based on the CPCTC theorem. This allows using previously proven congruent parts in future proofs.

1. Congruent
Triangles
Triangles are congruent when all
corresponding sides and interior angles are
congruent. The triangles will have the same
shape and size, but one may be a mirror
image of the other.

2. The Triangle Congruence
Postulates &Theorems
LAHALLHL
FOR RIGHT TRIANGLES ONLY
AASASASASSSS
FOR ALL TRIANGLES

3. SSS postulate
SSS (side, side, side) postulate
If three sides of a triangle are
congruent to its three corresponding
sides of another triangle, then the two
triangles are congruent.

4. AB ≅ ED ,
BC ≅ EF and
CA ≅ FD
∆ABC ≅ ∆DEF
Look at these two triangles

5. SAS postulate
SAS Postulate (Side-Angle-Side)
If two sides and the included
angle of one triangle are congruent
to the corresponding parts of another
triangle, then the triangles are
congruent.

6. Look at these triangles.
AC ≅ XZ
 C ≅  Z
CB ≅ ZY
∆ABC ≅ ∆XYZ

7. EXAMPLE 1
Write a proof.
GIVEN
PROVE
STATEMENTS REASONS
BC ≅ DA, BC AD
∆ABC ≅ ∆ CDA
1. Given1. BC ≅ DAS
Given2.2. BC AD
3. BCA ≅ DAC 3. Alternate Interior
Angles Theorem
A
4. 4.AC ≅ CA Reflexive propertyS

8. EXAMPLE 1
STATEMENTS REASONS
5. ABC ≅ CDA SAS Postulate5.

9. Given: RS  RQ and ST  QT
Prove: Δ QRT  Δ SRT.
Q
R
S
T
EXAMPLE 2

10. STATEMENT REASON ________
1. RS  RQ; ST  QT 1. Given
2. RT  RT 2. Reflexive
3. Δ QRT  Δ SRT 3. SSS Postulate
RQ S
T
EXAMPLE 2

11. ASA Postulate
ASA Postulate (Angle-Side-Angle)
If two angles and the included side
of one triangle are congruent to the
corresponding parts of another triangle,
then the triangles are congruent.

12. Look at these triangles.
 B ≅  E
BC ≅ EF
 C ≅  F
∆ABC ≅ ∆DEF

13. AAS Theorem
AAS (Angle-Angle-Side) Theorem
If two angles and a non-included
side of one triangle are congruent to two
angles and the corresponding non-
included side of a second triangle, then
the triangles are congruent.

14. Look at these triangles.
 B ≅  E
 C ≅  F
AC ≅ DF
∆ABC ≅ ∆DEF

15. Given: AD║EC, BD  BC
Prove: ∆ABD  ∆EBC
EXAMPLE 4

16. Statements:
1. BD  BC
2. AD ║ EC
3. D  C
4. ABD  EBC
5. ∆ABD  ∆EBC
Reasons:
1. Given
2. Given
3. If || lines, then alt. int.
s are 
4. Vertical Angles
Theorem
5. ASA Congruence
Postulate

17. EXAMPLE 5
GIVEN - EGF JGH, EF  HJ
PROVE - ∆EFG  ∆JHG

18. EXAMPLE 5
STATEMENTS REASONS
1. EFG JHG 1. Given
2. EF  HJ 2. Given
3. EGF JGH 3. Vertical angles
theorem
4. ∆EFG  ∆JHG 4. AAS Theorem

19. Given: YR  MA and AR  RM
Prove: Δ MYR  Δ AYR
Y A
R
M
Try to solve this.

20. CPCTC Theorem
•CPCTC states that if two
or more triangles are
proven congruent by any
method, then all of their
corresponding angles
and sides are congruent
as well.

21. Given: YR  MA and AR  RM
Prove: AY  MY
Y A
R
M
Try to solve this.

22. To prove that triangles are
congruent we are going to use these
theorems and postulates.
1.The (SSS) Side-Side-Side postulate
2.The (SAS) Side-Angle-Side postulate
3.The (ASA) Angle-Side-Angle
postulate
4.The (AAS) Angle-Angle-Side
theorem

23. 2. GIVEN; DE  CE, EA  EB
PROVE; ∆DAB  ∆CBA
1. GIVEN; circle with center
H
AHB   FHB
PROVE; A  F
H
A FB
D
E
C
B
A
Prove the following. ( 20 pts. )

24. Assignment
1.What is the HL theorem?
2.What is the LL theorem?
• Reference; Plane Geometry for Secondary Schools