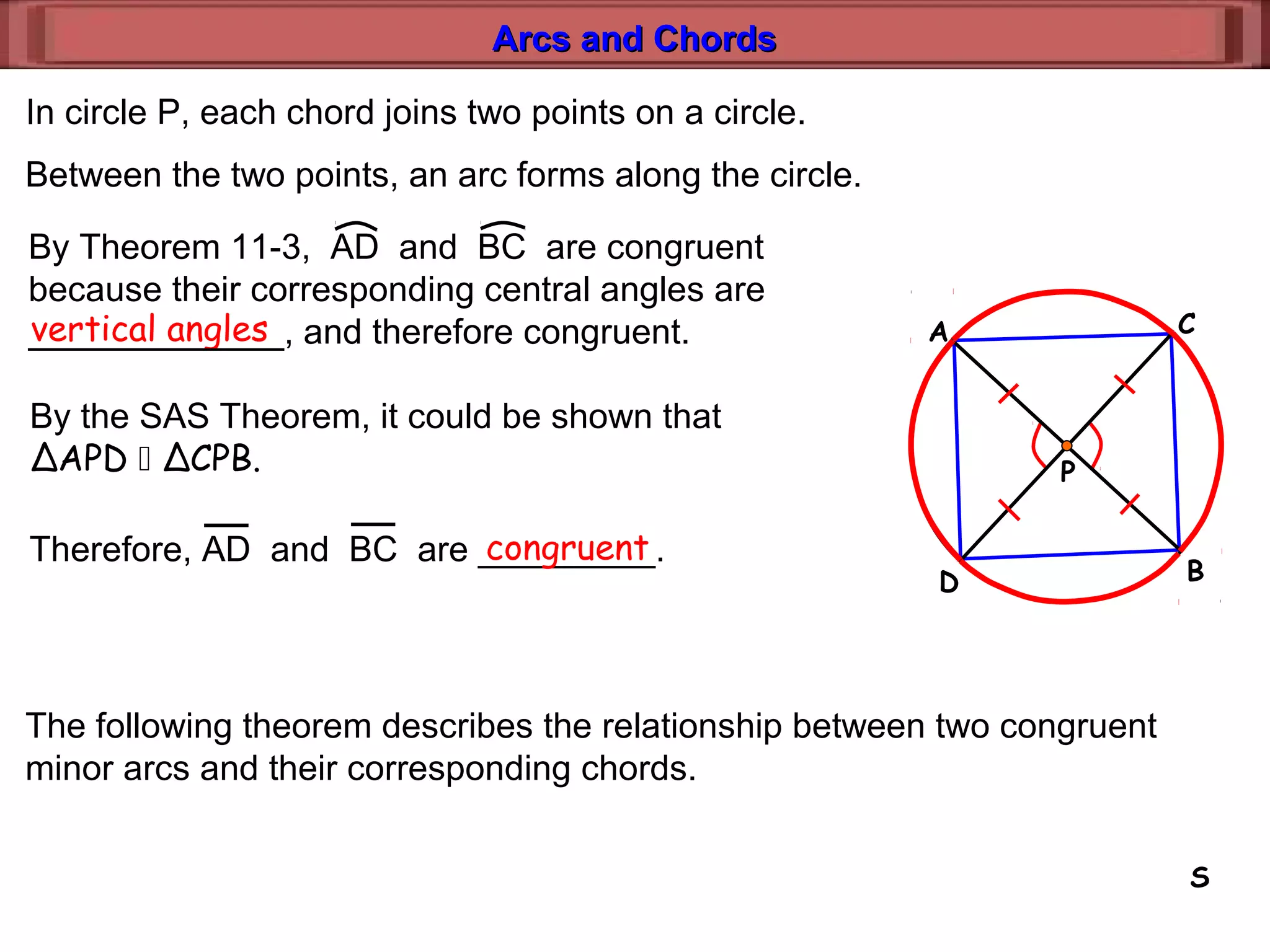
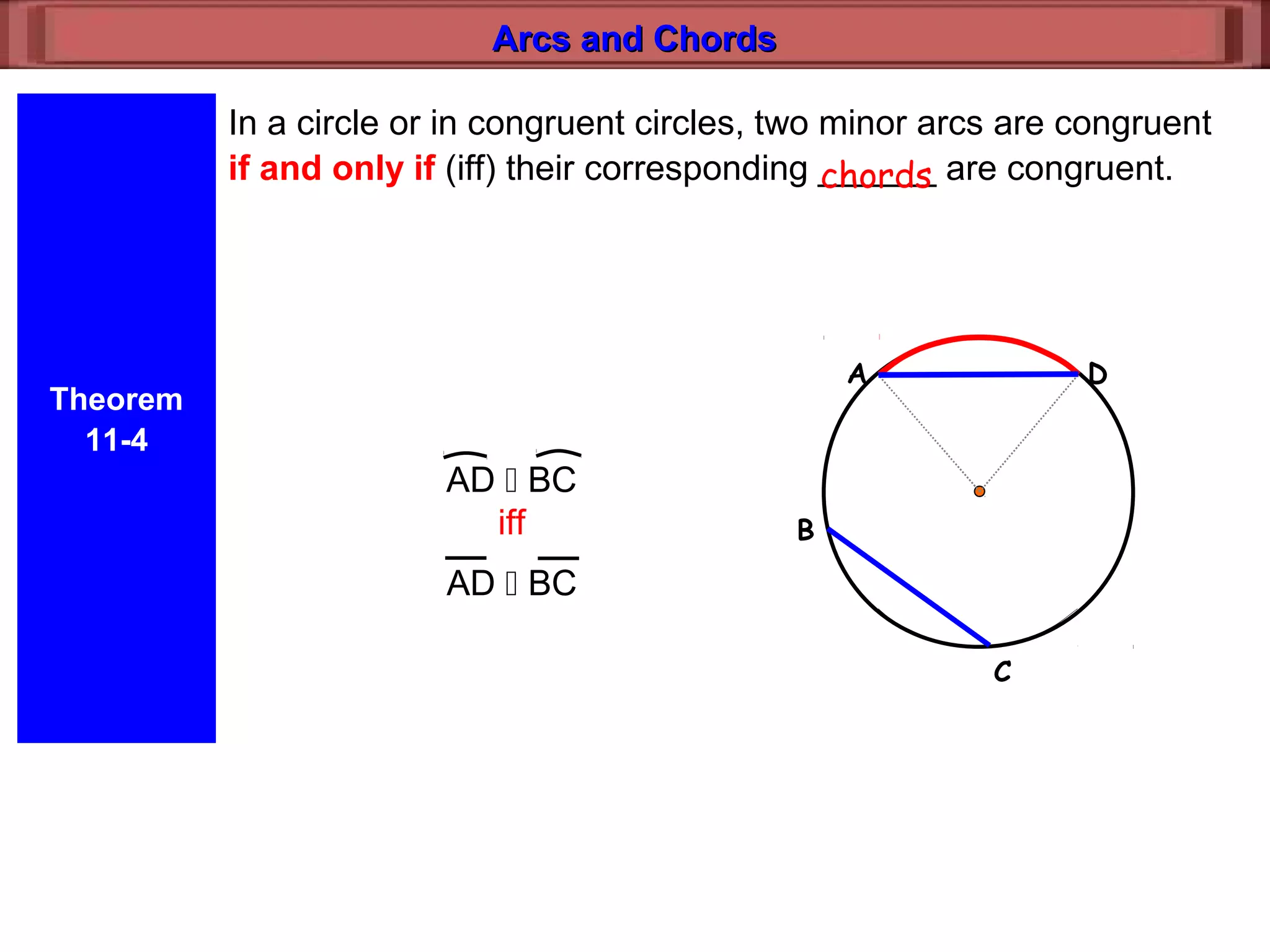
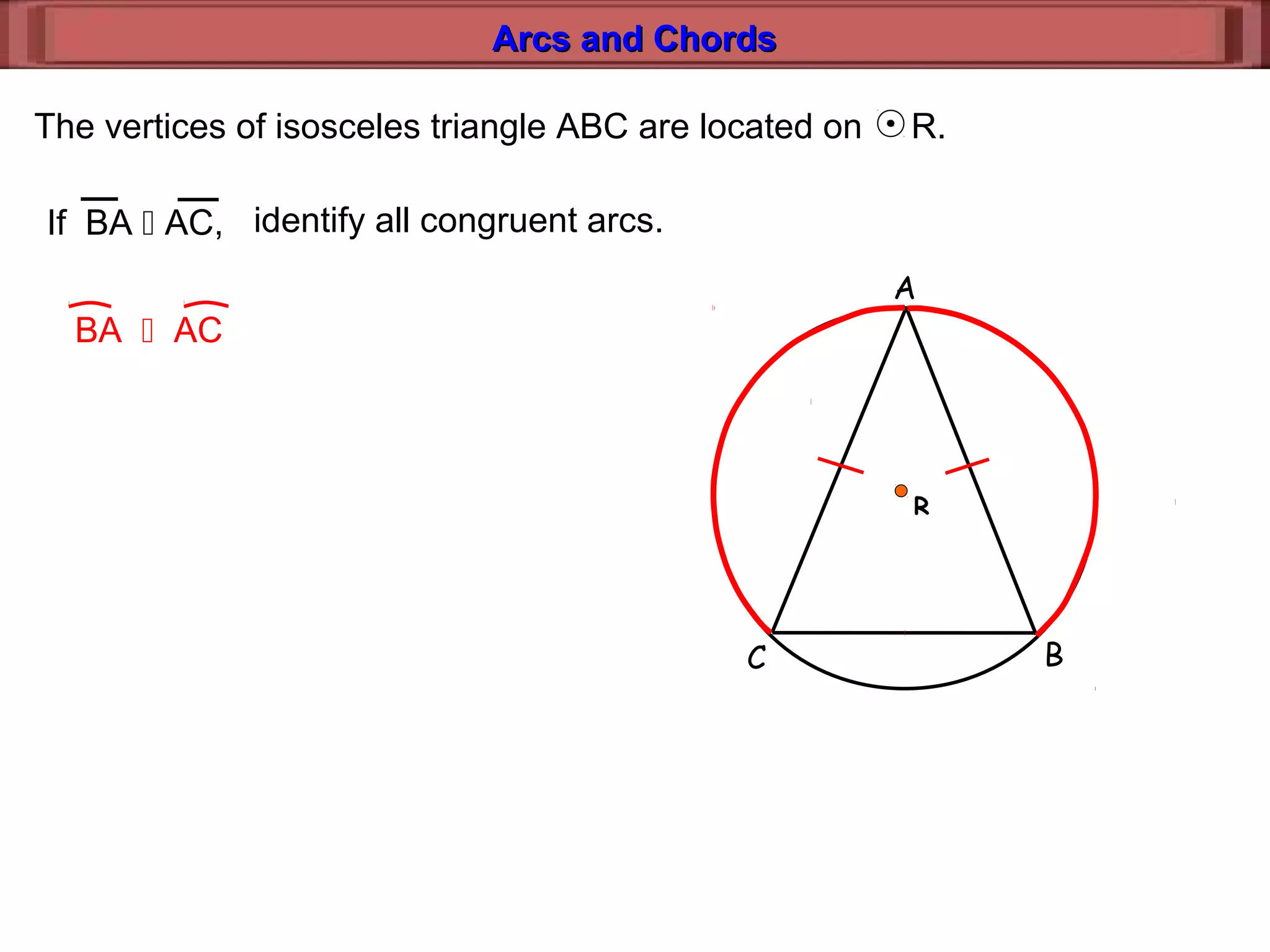
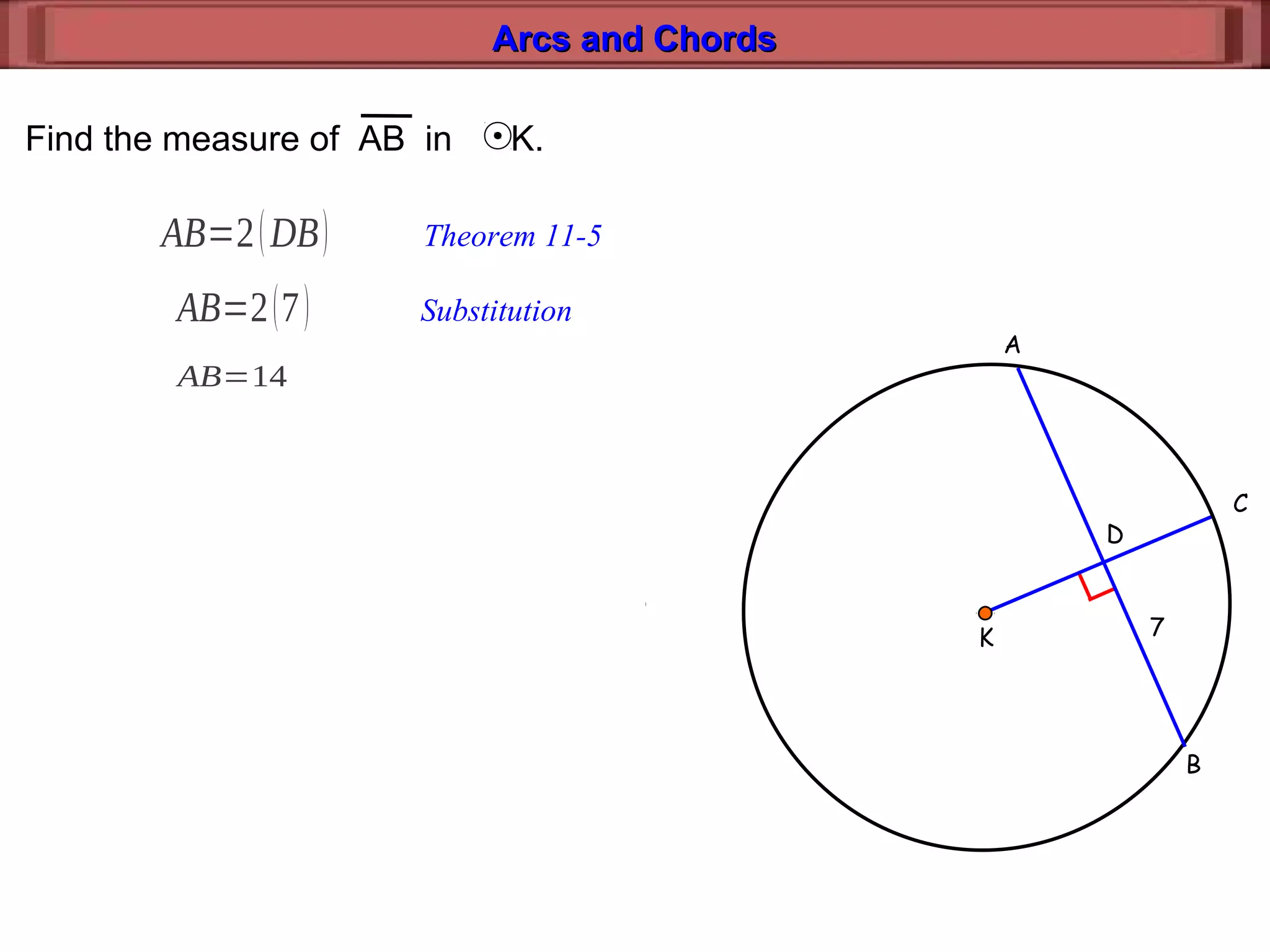
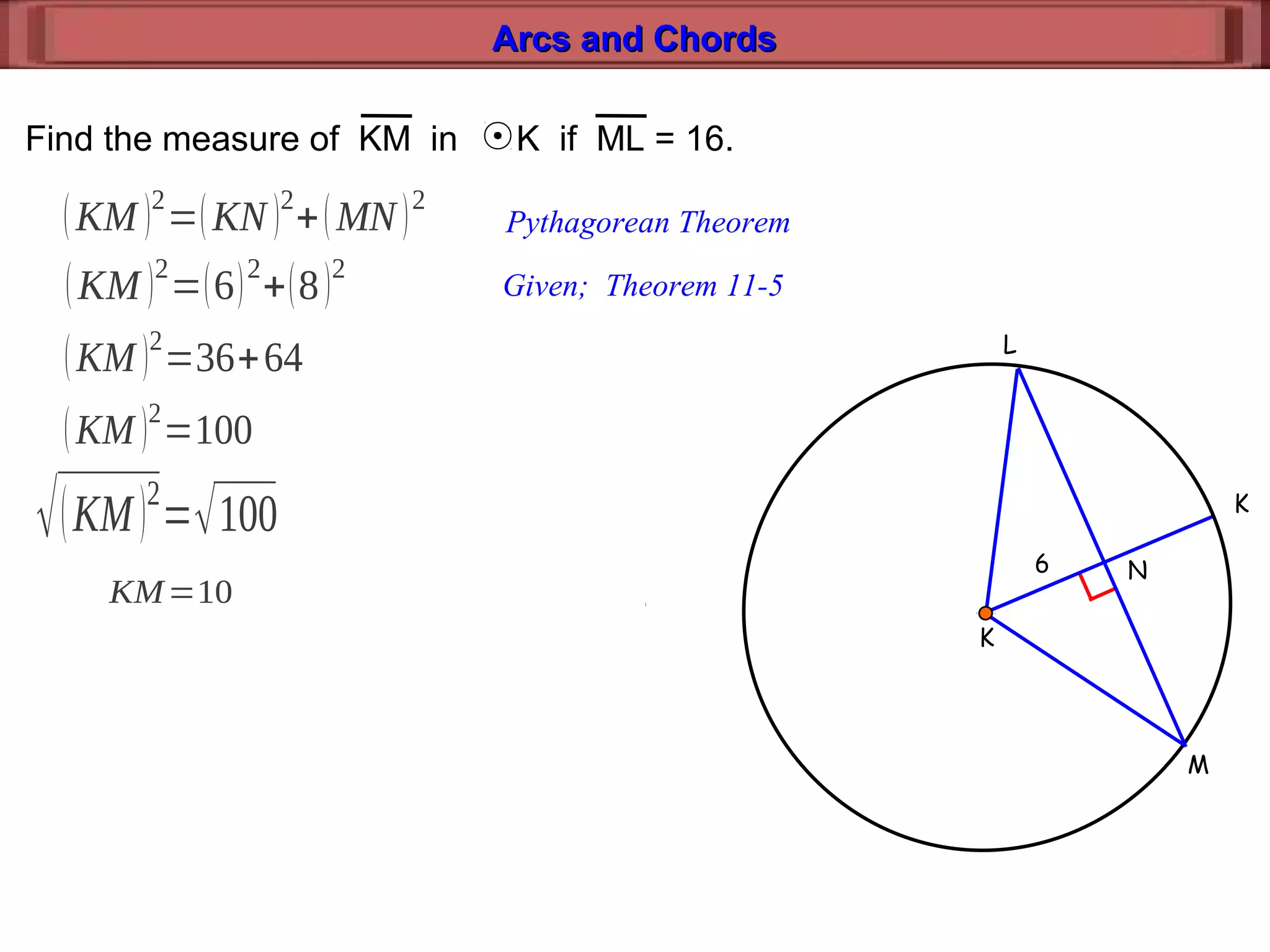
This document discusses relationships between arcs, chords, and diameters in circles. It defines arcs and chords, and presents theorems about congruent arcs having congruent chords, diameters bisecting chords and arcs if and only if they are perpendicular, and using properties of arcs, chords, and diameters to find unknown measures.

1. Arcs and ChordsArcs and Chords
You will learn to identify and use the relationships among
arcs, chords, and diameters.
Nothing New!

2. Arcs and ChordsArcs and Chords
BD
S
C
P
A
In circle P, each chord joins two points on a circle.
Between the two points, an arc forms along the circle.
vertical angles
By Theorem 11-3, AD and BC are congruent
because their corresponding central angles are
_____________, and therefore congruent.
By the SAS Theorem, it could be shown that
ΔAPD  ΔCPB.
Therefore, AD and BC are _________.congruent
The following theorem describes the relationship between two congruent
minor arcs and their corresponding chords.

3. Arcs and ChordsArcs and Chords
Theorem
11-4
In a circle or in congruent circles, two minor arcs are congruent
if and only if (iff) their corresponding ______ are congruent.
B
D
C
A
chords
AD  BC
iff
AD  BC

4. Arcs and ChordsArcs and Chords
A
BC
The vertices of isosceles triangle ABC are located on R.
R
If BA  AC, identify all congruent arcs.
BA  AC

5. Arcs and ChordsArcs and Chords
Step 1) Use a compass to draw circle on a
piece of patty paper. Label the
center P. Draw a chord that is not
a diameter. Label it EF.
Step 2) Fold the paper through P so that
E and F coincide. Label this fold
as diameter GH.
E
F
P
G
H
Q1: When the paper is folded, how do the lengths of EG and FG compare?
Q2: When the paper is folded, how do the lengths of EH and FH compare?
Q3: What is the relationship between diameter GH and chord EF?
EG  FG
EG  FG
They appear to be perpendicular.

6. Arcs and ChordsArcs and Chords
Theorem
11-5
In a circle, a diameter bisects a chord and its arc if and only if
(iff) it is perpendicular to the chord.
P
R
D
C
B
A
AR  BR and AD  BD
iff
CD AB
Like an angle, an arc can be bisected.

7. Arcs and ChordsArcs and Chords
B
C
A
K
D
7
Find the measure of AB in K.
AB=2(DB) Theorem 11-5
AB=2(7)
AB=14
Substitution

8. Arcs and ChordsArcs and Chords
M
K
L
K
N6
Find the measure of KM in K if ML = 16.
(KM )2
=(KN )2
+(MN)2
Pythagorean Theorem
(KM )2
=(6)2
+(8)2
Given; Theorem 11-5
(KM )2
=36+64
(KM )2
=100
√(KM)2
=√100
KM=10