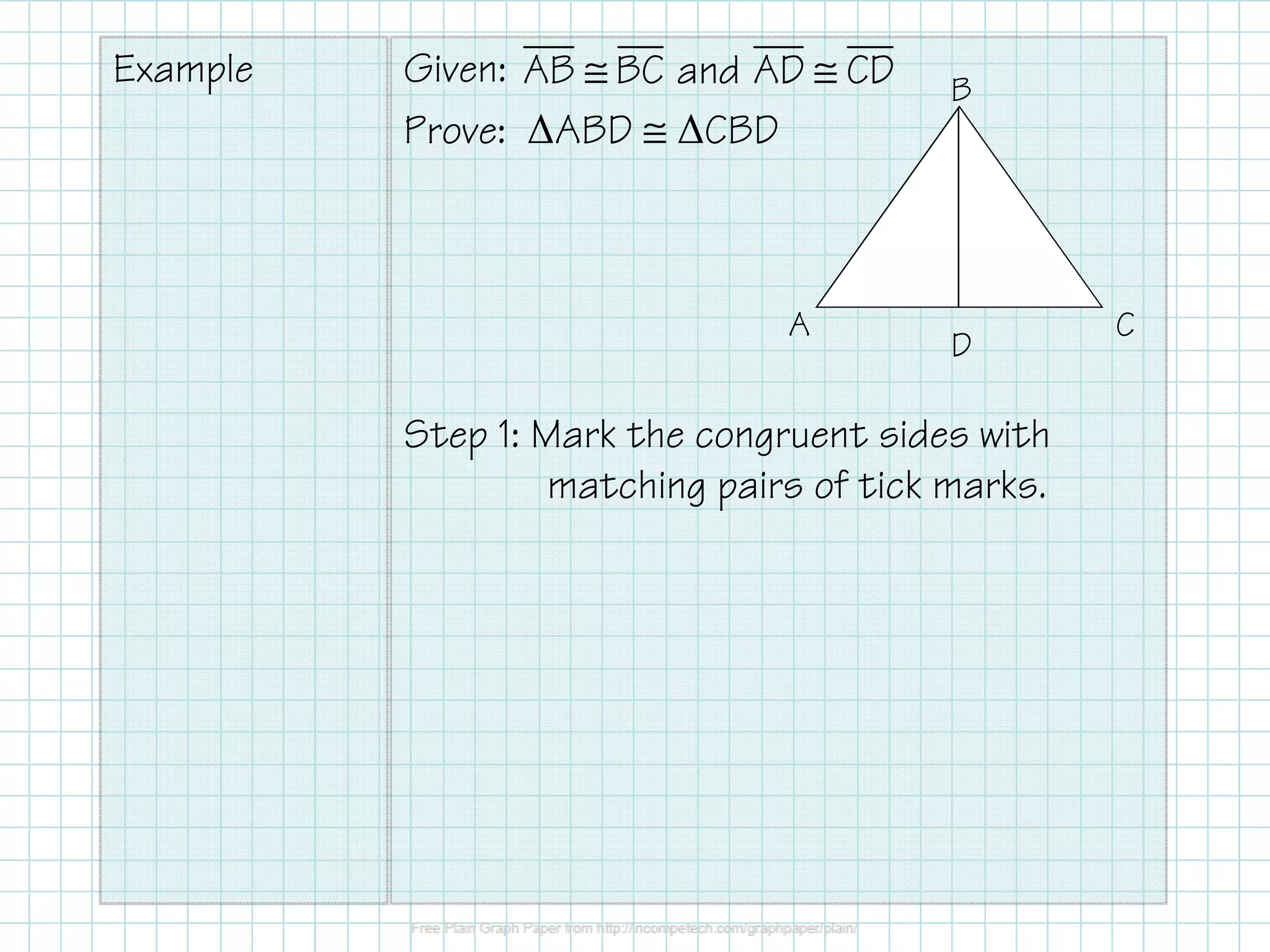
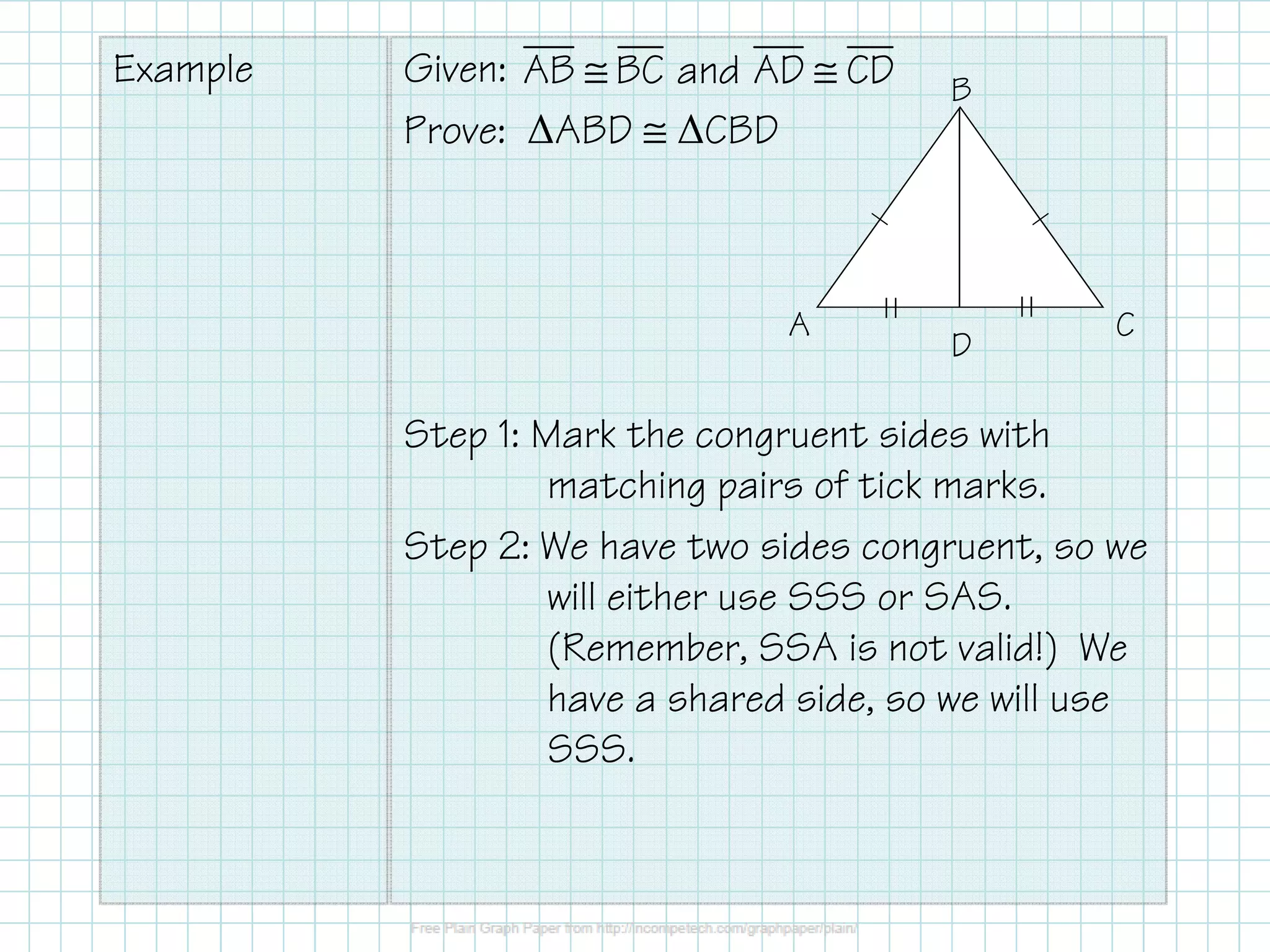
This document provides guidance on writing proofs to show that two triangles are congruent. It explains that a two-column proof lists given information, deduced information, and the statement to be proved, with reasons for each step. A basic three-step method is outlined: 1) Mark given information on the diagram, 2) Identify the congruence theorem and additional needed information, 3) Write the statements and reasons, with the last statement being what is to be proved. An example proof is provided using the Side-Side-Side congruence theorem to prove two triangles are congruent. Common theorems that can be used in proofs are also listed.

1. Congruent Triangle Proofs
The student is able to (I can):
• Create two-column proofs to show that two triangles are
congruent

2. When you are creating a proof, you list the
information that you are given, list any
other information you can deduce, and then
whatever it is you are trying to prove.
It is equally important that you give
reasons for each step that you list,
whether you are listing given information or
information you have deduced using
theorems and postulates.
While congruent triangle proofs can be a
little challenging, I have a basic three-step
method that I use to set them up.

3. Three Steps to a Proof
Step 1: Mark the given information on the
diagram
Step 2: Identify the congruence theorem
to be used and the additional
information needed and why.
Step 3: Write down the statements and
the reasons. Make sure your last
statement is what you are
supposed to be proving.

4. Example Given:
Prove: ∆ABD ≅ ∆CBD
Step 1: Mark the congruent sides with
matching pairs of tick marks.
AB BC and AD CD≅ ≅
A
B
C
D

5. Example Given:
Prove: ∆ABD ≅ ∆CBD
Step 1: Mark the congruent sides with
matching pairs of tick marks.
Step 2: We have two sides congruent, so we
will either use SSS or SAS.
(Remember, SSA is not valid!) We
have a shared side, so we will use
SSS.
AB BC and AD CD≅ ≅
A
B
C
D

6. Example Given:
Prove: ∆ABD ≅ ∆CBD
Step 3:
AB BC and AD CD≅ ≅
A
B
C
D
StatementsStatementsStatementsStatements ReasonsReasonsReasonsReasons
SSSS 1. 1. Given
SSSS 2. 2. Given
SSSS 3. 3. Refl. prop. ≅
4. ∆ABD ≅ ∆CBD 4. SSS
AB BC≅
AD CD≅
BD BD≅

7. Any theorem or postulate we have worked
with this year is fair game on a proof, but
here are the most common ones we will use:
• Reflexive property of congruence
(Refl. prop. ≅) (Use on shared sides)
• Vertical angles theorem (Vert. ∠s)
• Midpoint theorem (Midpt. thm)
• Any of the parallel line theorems
— Corresponding angles (Corr. ∠s)
— Alternate interior angles (Alt. int. ∠s)
— Alternate exterior angles (Alt.ext. ∠s)