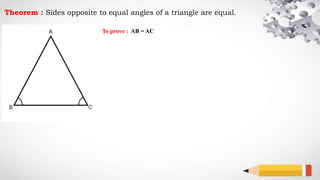
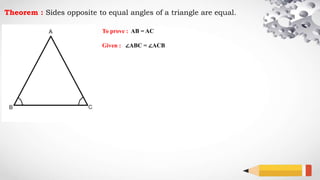
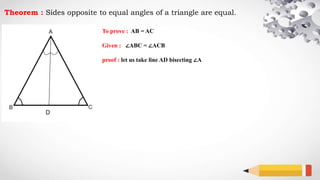
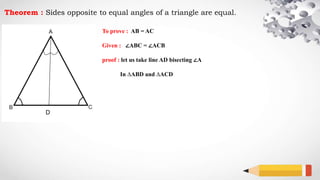
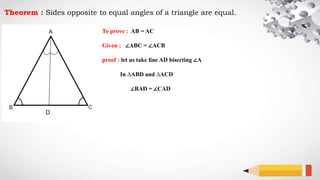
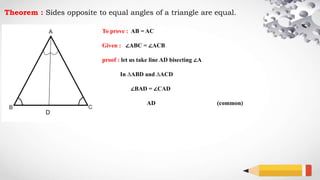
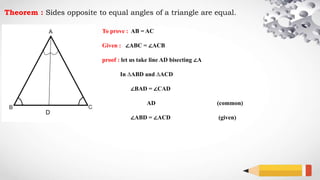
The document explains a geometric theorem stating that the sides opposite to equal angles in a triangle are equal, specifically proving that ab equals ac. The proof involves bisecting angle A and using the congruence of triangles ABD and ACD. The conclusion asserts that since the triangles are congruent, side lengths ab and ac are equal.

1. WE ARE ADDICTED TO LEARN

2. Name : Ramesh
Integrated B.Sc. - B.Ed.
School of education

3. Theorem : Sides opposite to equal angles of a triangle are equal.

4. Theorem : Sides opposite to equal angles of a triangle are equal.
To prove : AB = AC

5. Theorem : Sides opposite to equal angles of a triangle are equal.
To prove : AB = AC
Given : ∠ABC = ∠ACB

6. Theorem : Sides opposite to equal angles of a triangle are equal.
To prove : AB = AC
Given : ∠ABC = ∠ACB
proof : let us take line AD bisecting ∠A
D

7. Theorem : Sides opposite to equal angles of a triangle are equal.
To prove : AB = AC
Given : ∠ABC = ∠ACB
proof : let us take line AD bisecting ∠A
In ∆ABD and ∆ACD
D

8. Theorem : Sides opposite to equal angles of a triangle are equal.
To prove : AB = AC
Given : ∠ABC = ∠ACB
proof : let us take line AD bisecting ∠A
In ∆ABD and ∆ACD
∠BAD = ∠CAD
D

9. Theorem : Sides opposite to equal angles of a triangle are equal.
To prove : AB = AC
Given : ∠ABC = ∠ACB
proof : let us take line AD bisecting ∠A
In ∆ABD and ∆ACD
∠BAD = ∠CAD
AD (common)
D

10. Theorem : Sides opposite to equal angles of a triangle are equal.
To prove : AB = AC
Given : ∠ABC = ∠ACB
proof : let us take line AD bisecting ∠A
In ∆ABD and ∆ACD
∠BAD = ∠CAD
AD (common)
∠ABD = ∠ACD (given)
D

11. Theorem : Sides opposite to equal angles of a triangle are equal.
To prove : AB = AC
Given : ∠ABC = ∠ACB
proof : let us take line AD bisecting ∠A
In ∆ABD and ∆ACD
∠BAD = ∠CAD
AD (common)
∠ABD = ∠ACD (given)
∴ ∆ABD ≅∆ACD (AAS congruence rule rule)
D

12. Theorem : Sides opposite to equal angles of a triangle are equal.
To prove : AB = AC
Given : ∠ABC = ∠ACB
proof : let us take line AD bisecting ∠A
In ∆ABD and ∆ACD
∠BAD = ∠CAD
AD (common)
∠ABD = ∠ACD (given)
∴ ∆ABD ≅∆ACD (AAS congruence rule rule)
so, AB = AC (CPCT)
hence proved
D

13. Thank you