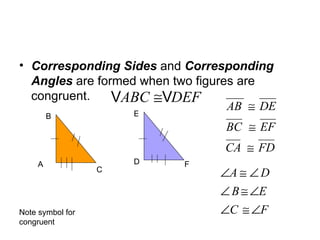
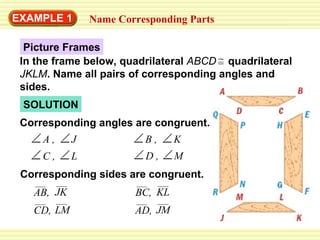
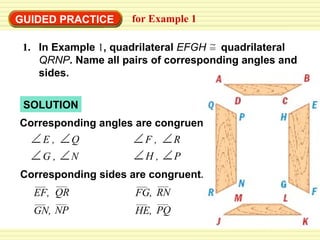
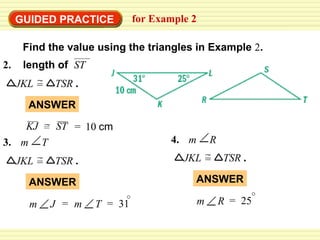
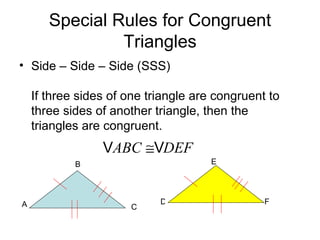
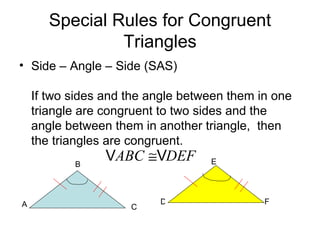
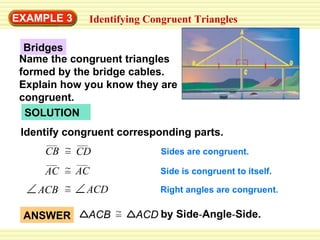
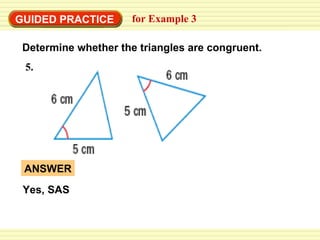
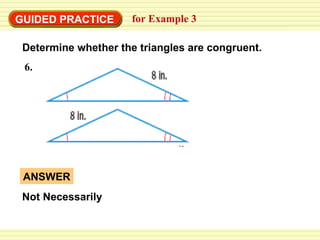
This document discusses identifying congruent polygons and triangles. It defines congruent polygons as having the same size and shape, with corresponding angles and sides being congruent. It provides examples of naming corresponding parts of congruent polygons and using properties of congruency to solve problems. Special rules for congruent triangles are given, including side-side-side, side-angle-side, and angle-side-angle. Students are directed to an online resource and practice problems are assigned.

1. Lesson 8.5 , For use with pages 427-432 Find the sum of the angle measures in the polygon. 1. octagon 2. 21 -gon

2. Lesson 8.5 , For use with pages 427-432 Find the sum of the angle measures in the polygon. 1. octagon 2. 21 -gon ANSWER 3420º ANSWER 1080º

3. Congruent Polygons Section 8.5 P. 427 - 432

7. Picture Frames EXAMPLE 1 Name Corresponding Parts SOLUTION Corresponding angles are congruent. Corresponding sides are congruent. = In the frame below, quadrilateral ABCD quadrilateral JKLM . Name all pairs of corresponding angles and sides. A , B , K D , M J C , L AB, JK CD, LM BC, KL AD, JM

8. GUIDED PRACTICE for Example 1 SOLUTION Corresponding angles are congruent. Corresponding sides are congruent. 1. In Example 1 , quadrilateral EFGH quadrilateral QRNP . Name all pairs of corresponding angles and sides. = E , F , R H , P Q G , N EF, QR GN, NP FG, RN HE, PQ

9. SOLUTION EXAMPLE 2 Using Congruent Polygons Corresponding angles are congruent. Add. Subtract 56 from each side. Simplify. ANSWER JKL TSR . = Find m S . 31 + m K + 25 = 180 K and S are corresponding angles, so they have the same measure. Find m K . Sum of angle measures is 180 . = 180 m K + 56 m K + 56 – 56 = 180 – 56 m K = 124 = Because m K m S, m S = 124

10. GUIDED PRACTICE for Example 2 Find the value using the triangles in Example 2 . 2. length of ST KJ ST = 10 cm ANSWER JKL TSR . = 3. m T m J = m T = 31 ANSWER JKL TSR . = 4. m R m R = 25 ANSWER JKL TSR . =

16. SOLUTION EXAMPLE 3 Identifying Congruent Triangles Bridges Identify congruent corresponding parts. Sides are congruent. Side is congruent to itself. Right angles are congruent. ANSWER Name the congruent triangles formed by the bridge cables. Explain how you know they are congruent. CB = CD AC AC = = ACB ACD ACB ACD = by Side - Angle - Side.

17. GUIDED PRACTICE for Example 3 Determine whether the triangles are congruent. 5. Yes, SAS ANSWER

18. GUIDED PRACTICE for Example 3 Determine whether the triangles are congruent. 6. Not Necessarily ANSWER