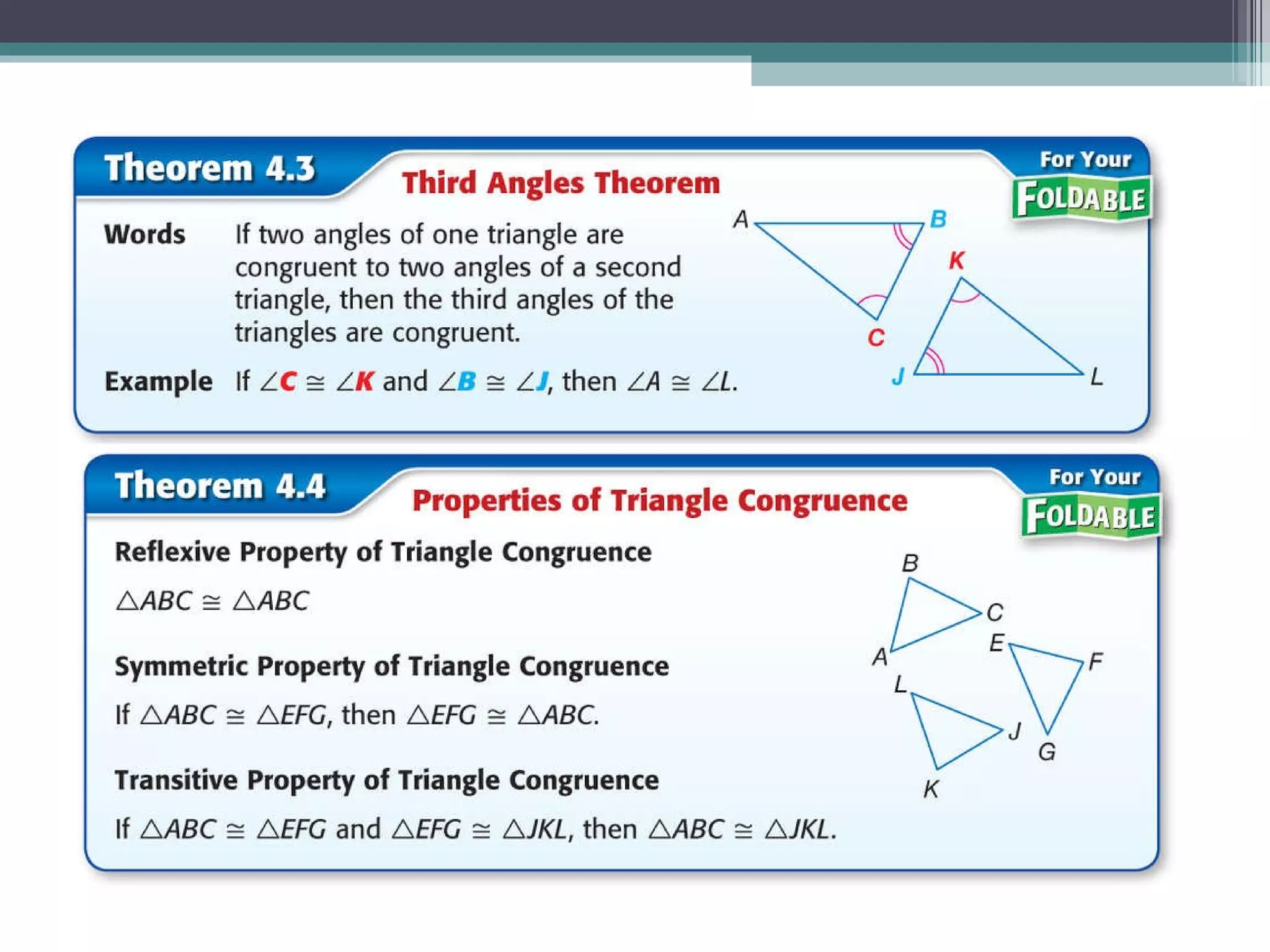
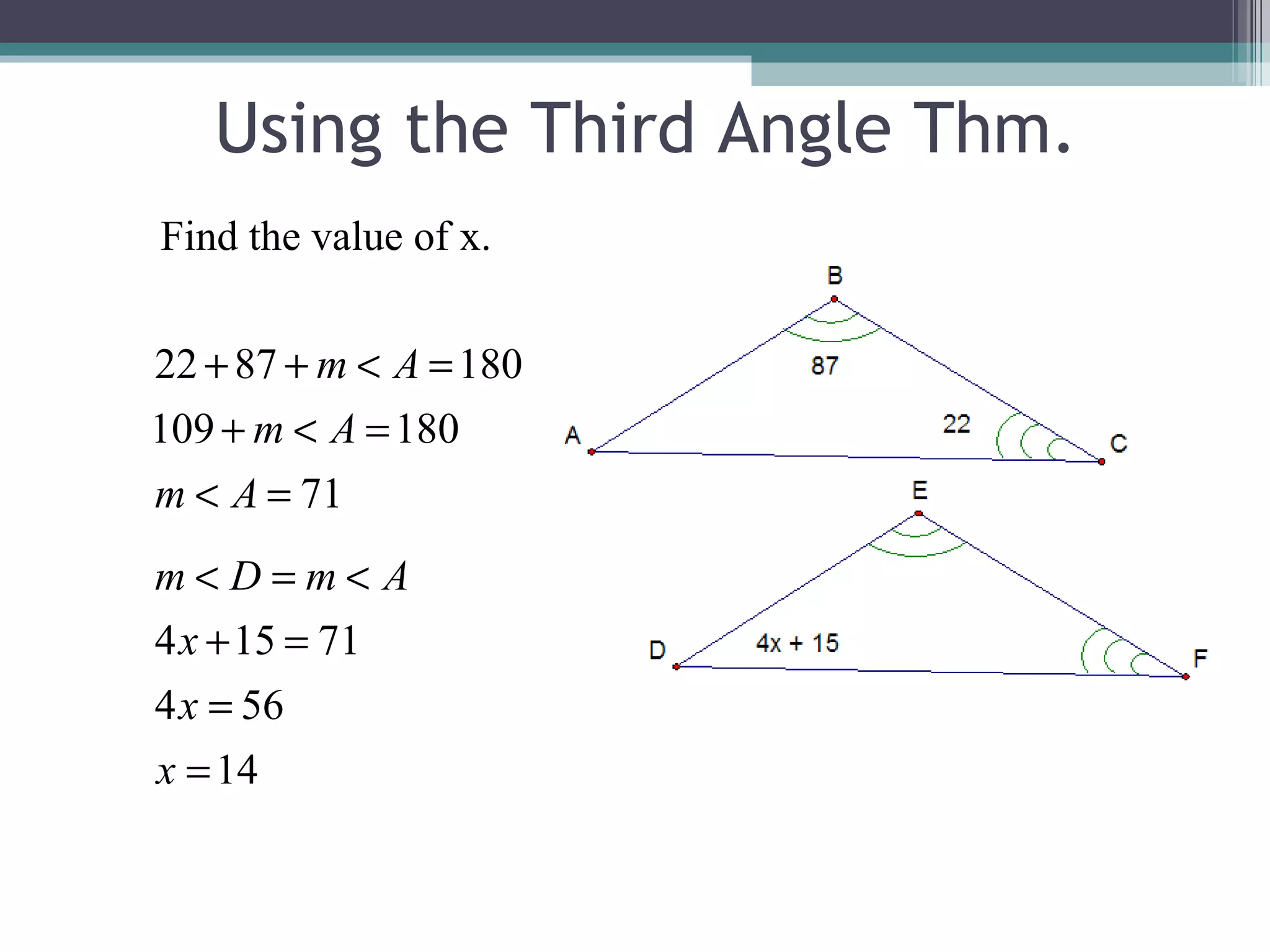
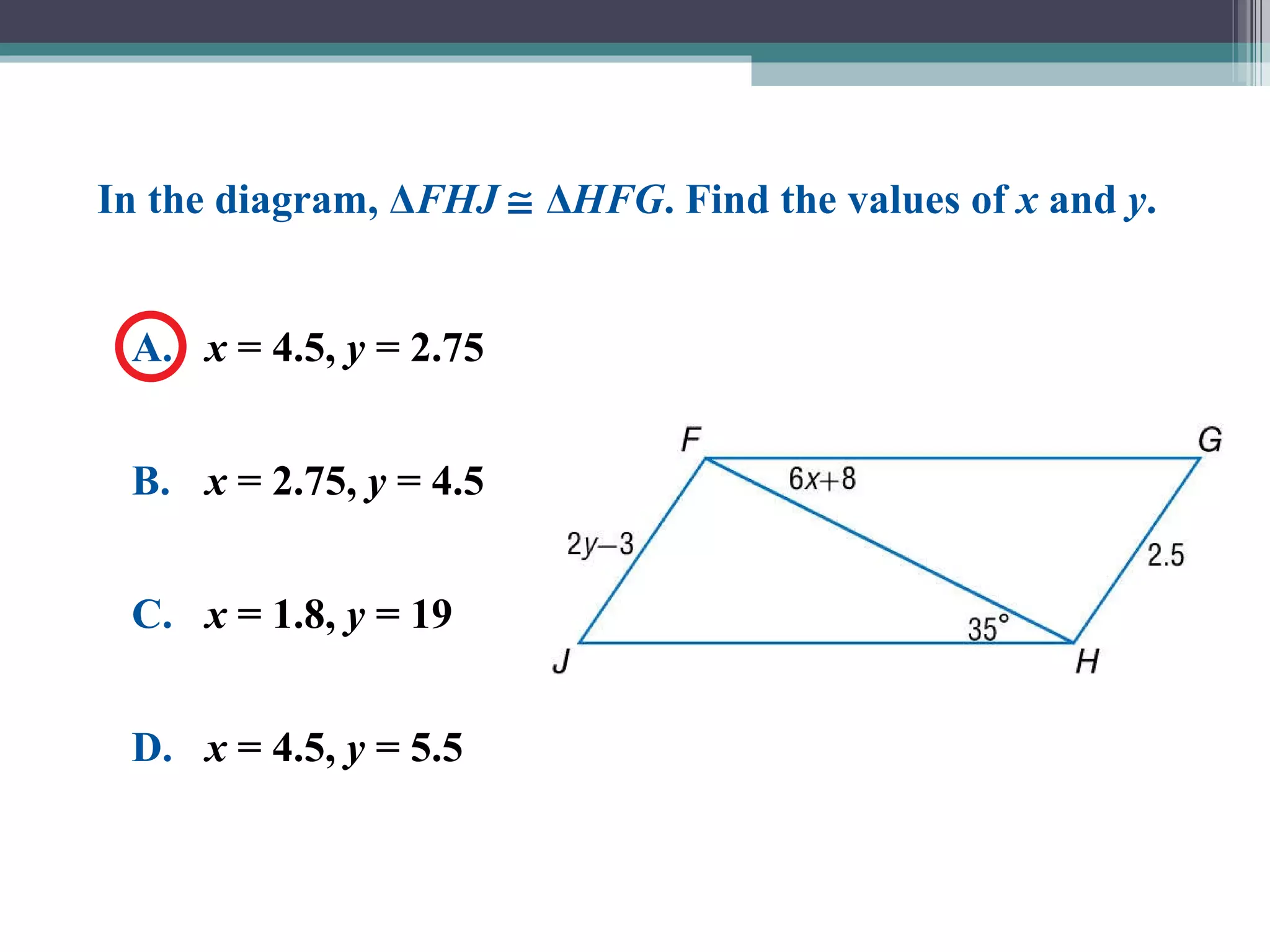
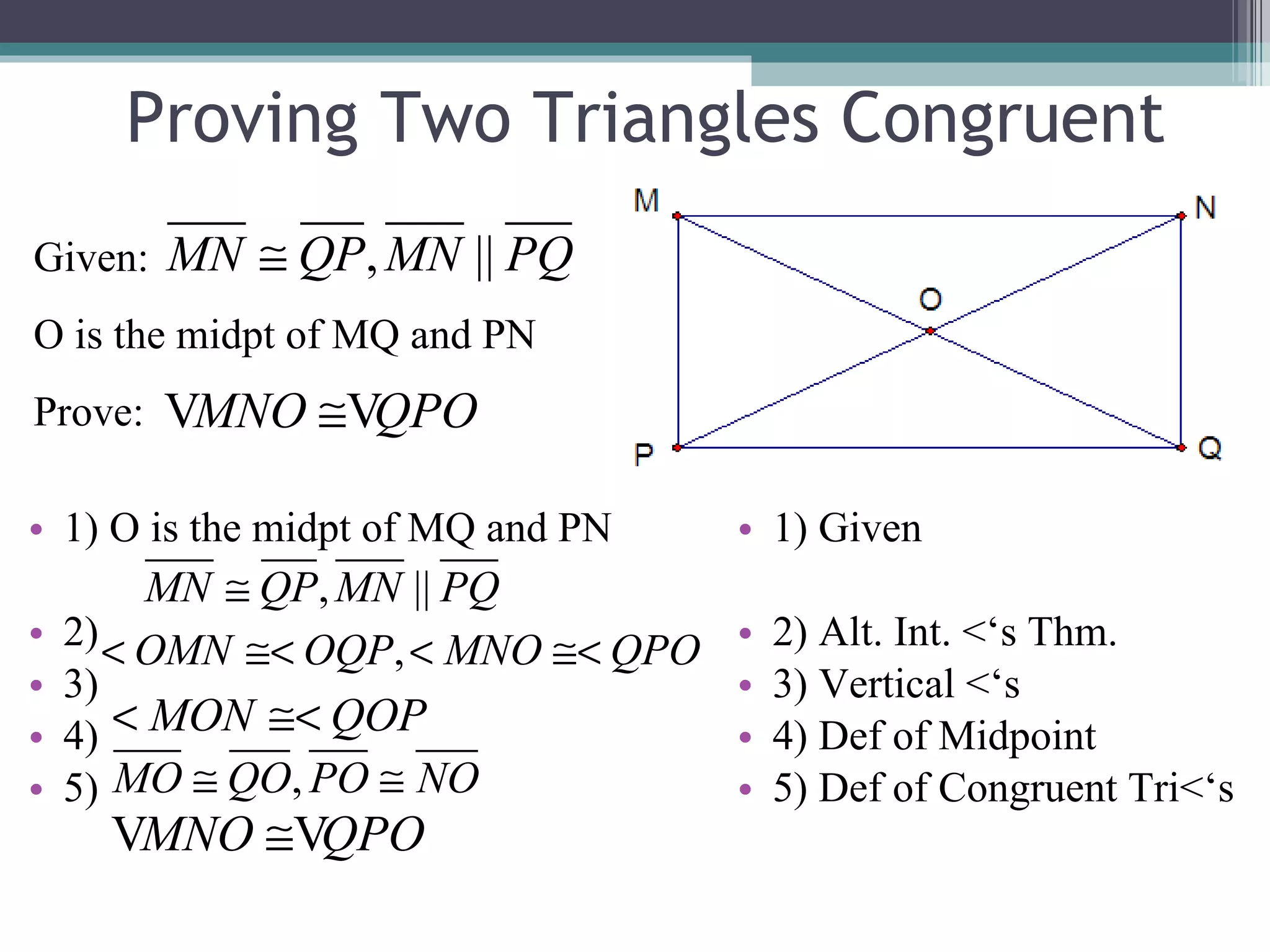
The document discusses congruent triangles and their properties. It defines congruent figures as those with corresponding sides and angles that are congruent. It presents several ways to prove triangles are congruent, including using corresponding parts, vertical angles, the third angle theorem, and properties of congruent figures like the transitive property. It provides examples of writing congruence statements and determining if triangles are congruent based on given information.

1. Geometry - 4.3 Congruent Triangles

2. Congruent, Corresponding Angles/Sides Two figures are congruent when their corresponding sides and corresponding angles are congruent. Corresponding Angles Corresponding Sides There is more than one way to write a congruence statement, but the you must list the corresponding angles in the same order.

4. Naming Congruent Parts Write a congruence statement for the triangles below. Identify all pairs of congruent parts. Corresponding Angles Corresponding Sides

5. Identify Corresponding Congruent Parts Show that the polygons are congruent by identifying all of the congruent corresponding parts. Then write a congruence statement. Answer: All corresponding parts of the two polygons are congruent. Therefore, ABCDE  RTPSQ . Sides: Angles:

6. Third Angle Thm Third Angle Thm. - If two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent. If and then,

7. Properties of Congruent Triangles Transitive Property of Congruent Triangles Reflexive Property of Congruent Triangles Symmetric Property of Congruent Triangles

9. Proof of Third Angle Thm 1) 2) m<A = m<D, m<B = m<E 3) m<A + m<B + m<C = 180 4) m<D + m<E + m<F = 180 5) m<A + m<B + m<C = m<D + m<E + m<F 6) m<C = m<F 7) 1) Given 2) Def of congruent angles 3) Triangle Sum Thm 4) Triangle Sum Thm 5) Substitution 6) Subtraction 7) Def of congruent angles and Given: Prove:

10. Using the Third Angle Thm. Find the value of x.

11. Determining Triangle Congruency Decide whether the triangles are congruent. Justify your reasoning. From the diagram all corresponding sides are congruent and that <F and <H are congruent. <EGF and <HGJ are congruent because of Vertical angles. <E and <J are congruent because of the third angle theorem Since all of the corresponding sides and angles are congruent,

12. Using Properties of Congruent Figures In the diagram, Find the value of x. Find the value of y.

13. Use Corresponding Parts of Congruent Triangles In the diagram, Δ ITP  Δ NGO . Find the values of x and y .  O   P 6 y – 14 = 40 6 y = 54 y = 9 x – 2 y = 7.5 x – 2(9) = 7.5 x – 18 = 7.5 x = 25.5 Answer: x = 25.5, y = 9

14. A. x = 4.5, y = 2.75 B. x = 2.75, y = 4.5 C. x = 1.8, y = 19 D. x = 4.5, y = 5.5 In the diagram, Δ FHJ  Δ HFG . Find the values of x and y .

15. Proof: Prove: Δ LMN  Δ PON 2.  LNM   PNO 2. Vertical Angles Theorem Statements Reasons 3.  M   O 3. Third Angles Theorem 4. Δ LMN  Δ PON 4. Def of Congruent Triangles 1. Given 1.

16. Proving Two Triangles Congruent 1) O is the midpt of MQ and PN 2) 3) 4) 5) 1) Given 2) Alt. Int. <‘s Thm. 3) Vertical <‘s 4) Def of Midpoint 5) Def of Congruent Tri<‘s Given: O is the midpt of MQ and PN Prove:

17. Practice Problems Pg.257 #8,9-15(odds),19-23(odds),24 HW Check Next Class