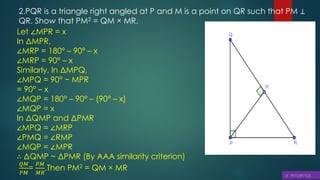
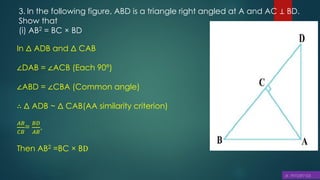
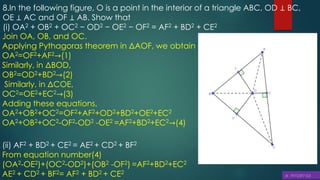
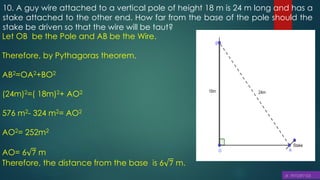
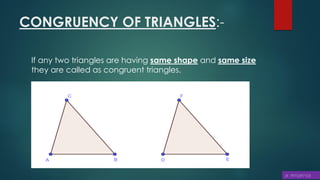
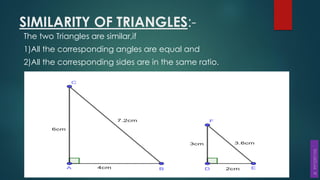
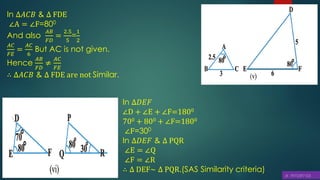
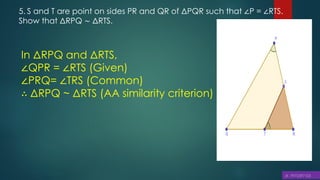
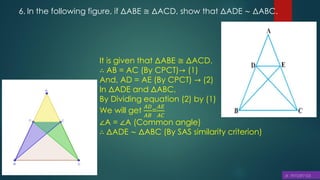
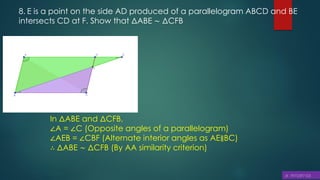
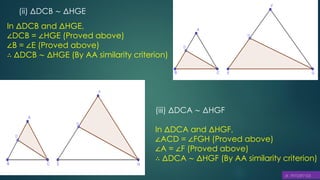
This document discusses triangles, similarity, and proportionality. It defines triangles, congruent triangles, and similar figures. It states that two polygons are similar if corresponding angles are equal and corresponding sides are in the same ratio. It introduces the Basic Proportionality Theorem, which states that if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally. It also discusses the converse of this theorem and criteria for similarity of triangles based on equal angles.



















![10.The diagonals of a quadrilateral ABCD intersect each other at the
point O such that
𝐴𝑂
𝐵𝑂
=
𝐶𝑂
𝐷𝑂
.Show that ABCD is a trapezium.
Let us draw a line EF∥ 𝐴𝐵 passing through point o.
Given
𝐴𝑂
𝐵𝑂
=
𝐶𝑂
𝐷𝑂
⟹
𝐴𝑂
𝐶𝑂
=
𝐵𝑂
𝐷𝑂
⇢ (1)
In ∆ADB, EO∥ AB,Then,
𝐴𝐸
𝐷𝐸
=
𝐵𝑂
𝐷𝑂
⇒
𝐴𝐸
𝐷𝐸
=
𝐴𝑂
𝐶𝑂
[from (1)]
In ∆ADC.
Line EO divides the triangle in the same ratio.
∴ EO∥ DC.
Now, EO∥ DC.But we know that EO∥ AB. ⇒ EO∥ D𝐶 ∥AB
⇒ AB∥ D𝐶.One pair of opposite sides of ABCD are
parallel.
∴ ABCD is a trapezium.](https://image.slidesharecdn.com/trianglespptbyjk-200505104945/85/Triangles-ppt-by-jk-22-320.jpg)















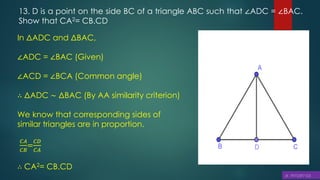

![Similarly, we can prove that quadrilateral PQLR is a
parallelogram and PR = QL, PQ = LR
It was given that ,
𝐴𝐵
𝑃𝑄
=
𝐴𝐶
𝑃𝑅
=
𝐴𝐷
𝑃𝑀
⟹
𝐴𝐵
𝑃𝑄
=
𝐵𝐸
𝑄𝐿
=
2𝐴𝐷
2𝑃𝑀
⟹
𝐴𝐵
𝑃𝑄
=
𝐵𝐸
𝑄𝐿
=
𝐴𝐸
𝑃𝐿
∴ ΔABE ∼ ΔPQL (By SSS similarity criterion)
We know that corresponding angles of similar
triangles are equal. ∴ ∠BAE = ∠QPL⟶(1)
Similarly, it can be proved that ΔAEC ∼ ΔPLR and
∠CAE = ∠RPL ⟶(2)
Adding equation (1) and (2), we obtain
∠BAE + ∠CAE = ∠QPL + ∠RPL
⇒ ∠CAB = ∠RPQ ⟶(3)
In ΔABC and ΔPQR,
𝐴𝐵
𝑃𝑄
=
𝐴𝐶
𝑃𝑅
(Given)
∠CAB = ∠RPQ [Using equation (3)]
∴ ΔABC ∼ ΔPQR (By SAS similarity criterion)](https://image.slidesharecdn.com/trianglespptbyjk-200505104945/85/Triangles-ppt-by-jk-46-320.jpg)

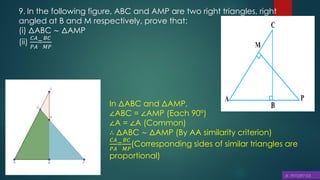
![16. If AD and PM are medians of triangles ABC and PQR, respectively
where ΔABC ∼ ΔPQR Prove that
𝐴𝐵
𝑃𝑄
=
𝐴𝐷
𝑃𝑀
It is given that ΔABC ∼ ΔPQR
We know that the corresponding sides of similar
triangles are in proportion. ∴
𝐴𝐵
𝑃𝑄
=
𝐴𝐶
𝑃𝑅
=
𝐵𝐶
𝑄𝑅
⟶(1)
Also, ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R ⟶ (2)
Since AD and PM are medians, they will divide their
opposite sides.
∴BD=
𝐵𝐶
2
& QM=
𝑄𝑅
2
⟶(3)
From equations (1) and (3), we obtain
𝐴𝐵
𝑃𝑄
=
𝐵𝐷
𝑄𝑀
⟶(4)
In ΔABD and ΔPQM,
∠B = ∠Q [Using equation (2)]
𝐴𝐵
𝑃𝑄
=
𝐵𝐷
𝑄𝑀
[Using equation (4)]
∴ ΔABD ∼ ΔPQM (By SAS similarity criterion)
𝐴𝐵
𝑃𝑄
=
𝐵𝐷
𝑄𝑀
=
𝐴𝐷
𝑃𝑀](https://image.slidesharecdn.com/trianglespptbyjk-200505104945/85/Triangles-ppt-by-jk-48-320.jpg)
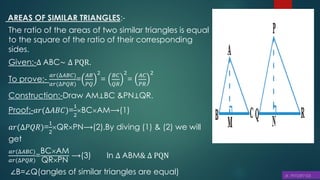
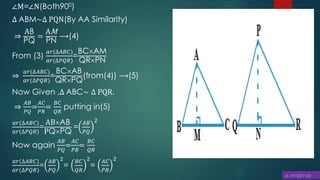




![5.D, E and F are respectively the mid-points of sides AB, BC and CA of
ΔABC. Find the ratio of the area of ΔDEF and ΔABC.
D and E are the mid-points of ΔABC.
∴DE∥AC and DE =
1
2
AC
In ΔBED and ΔBCA,
∠BED = ∠BCA (Corresponding angles)
∠BDE = ∠BAC (Corresponding angles)
∠EBA = ∠CBA (Common angles)
∴ ΔBED ~ ΔBCA (AAA similarity criterion)
Wkt
𝑎𝑟(∆𝐵𝐸𝐷)
𝑎𝑟(∆𝐵𝐶𝐴)
=
𝐷𝐸
𝐴𝐶
2
⇒
𝑎𝑟(∆𝐵𝐸𝐷)
𝑎𝑟(∆𝐵𝐶𝐴)
=
1
4
⇒ 𝑎𝑟(∆𝐵𝐸𝐷)=
1
4
𝑎𝑟(∆𝐵𝐶𝐴)
Similarly, 𝑎𝑟 ∆𝐶𝐹𝐸 =
1
4
𝑎𝑟(∆𝐵𝐶𝐴)
& 𝑎𝑟 ∆𝐴𝐷𝐹 =
1
4
𝑎𝑟(∆𝐵𝐶𝐴)
& Also, 𝑎𝑟 ∆𝐷𝐸𝐹 = 𝑎𝑟(∆𝐵𝐶𝐴)-[𝑎𝑟(∆𝐵𝐸𝐷)+ 𝑎𝑟 ∆𝐶𝐹𝐸 + 𝑎𝑟 ∆𝐴𝐷𝐹 ]
𝑎𝑟 ∆𝐷𝐸𝐹 = 𝑎𝑟(∆𝐵𝐶𝐴)-
3
4
𝑎𝑟(∆𝐵𝐶𝐴)=
1
4
𝑎𝑟(∆𝐵𝐶𝐴) ⇒
𝑎𝑟(∆𝐷𝐸𝐹)
𝑎𝑟(∆𝐵𝐶𝐴)
=
1
4](https://image.slidesharecdn.com/trianglespptbyjk-200505104945/85/Triangles-ppt-by-jk-55-320.jpg)

![In ΔABD and ΔPQS,
∠B = ∠Q [Using equation (2)]
And,
𝐴𝐵
𝑃𝑄
=
𝐵𝐷
𝑄𝑆
[Using equation (3)]
∴ ΔABD ∼ ΔPQS (SAS similarity criterion)
Therefore, it can be said that
𝐴𝐵
𝑃𝑄
=
𝐵𝐷
𝑄𝑆
=
𝐴𝐷
𝑃𝑆
⟶(4)
𝑎𝑟(∆𝐴𝐵𝐶)
𝑎𝑟(∆𝑃𝑄𝑅)
=
𝐴𝐵
𝑃𝑄
2
=
𝐵𝐶
𝑄𝑅
2
=
𝐴𝐶
𝑃𝑅
2
From equations (1) and (4), we may find that
𝐴𝐵
𝑃𝑄
=
𝐵𝐶
𝑄𝑅
=
𝐴𝐶
𝑃𝑅
=
𝐴𝐷
𝑃𝑆
And hence,
𝑎𝑟(∆𝐴𝐵𝐶)
𝑎𝑟(∆𝑃𝑄𝑅)
=
𝐴𝐷
𝑃𝑆
2](https://image.slidesharecdn.com/trianglespptbyjk-200505104945/85/Triangles-ppt-by-jk-57-320.jpg)


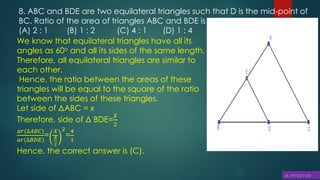





![Now, in ΔABC and ΔPQR,
AB = PQ (By construction)
BC = QR (By construction)
AC = PR [Proved in (3) above]
So, ΔABC≅ΔPQR (SSS congruence)
Therefore, ∠B = ∠Q (CPCT)
But ∠Q = 90° (By construction)
So, ∠B = 90°](https://image.slidesharecdn.com/trianglespptbyjk-200505104945/85/Triangles-ppt-by-jk-66-320.jpg)