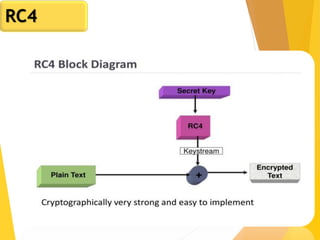
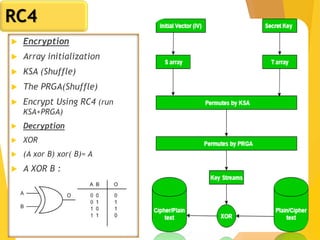
The document outlines key concepts in network security, focusing on random number generation types and algorithms like the RC4 cipher. It delves into basic number theory, including modular arithmetic and important mathematical properties essential for cryptography. The discussion includes notable mathematical principles such as Fermat's Little Theorem and Euler's Totient Function, highlighting their significance in cryptographic practices.





![7
Uniformity: If the interval [0,1] is divided into n
classes, or subintervals of equal length, the expected
number of observations in each interval is N/n, where
N is the total number of observations
Independence: The probability of observing a value in
a particular interval is independent of the previous
value drawn
Properties of Random Numbers](https://image.slidesharecdn.com/ntewroksecuirtycs3-4-200126155251/85/Network-Security-CS3-4-7-320.jpg)


















































![62
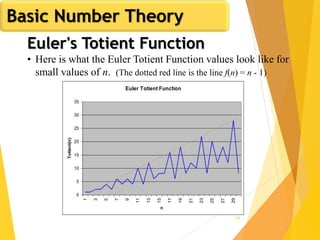
Euler's Totient Function
Assume we have two distinct prime numbers, p and q,
and an integer n = pq
Then:
The set of residues in Zn i s{0,1,...,(pq - 1)}
The residues that are not relatively prime to n are:
The set {p, 2p, ... ,(q - 1)p}, the set {q, 2q, ... ,(p - 1)q}, and
0
So:
)1()1()(φ)(φ)(φ)(φ qpqppqn
)(φ)(φ
)1()1(
1)(
]1)1()1[()(φ
qp
qp
qppq
pqpqn
Basic Number Theory](https://image.slidesharecdn.com/ntewroksecuirtycs3-4-200126155251/85/Network-Security-CS3-4-62-320.jpg)