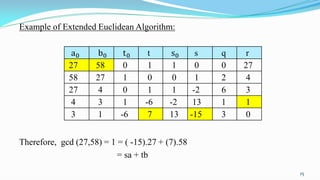
This document presents an overview of number theory, covering its definitions, applications, and relevant concepts such as modular arithmetic, congruences, and cryptography. It also discusses various algorithms including Euclid's algorithm and the extended Euclidean algorithm, alongside examples to illustrate these principles. The document emphasizes the applications of number theory in fields like cryptography and coding theory, providing insights into mathematical processes like the Chinese Remainder Theorem and different ciphers.

1. Presented by
ITISHREE DASH
Assistant Professor in Mathematics
Department of Basic Science and Humanities
Gandhi Institute for Education and Technology, Baniatangi, Odisha
1

2. CONTENTS
 Introduction
 Applications
 Modular Arithmetic
 Congruence and Pseudorandom Number
 Congruence and CRT(Chinese Remainder Theorem)
 Congruence and Cryptography
 Summary
 References
2

3. INTRODUCTION
Number theory is the study of the set of natural number and relationship between different sorts of
number.
• Odd 1, 3, 5, 7……………
• Even 2, 4, 6, 8……………
• Square 1, 4, 9, 16………….
• Cube 1, 8, 27, 64………..
• Prime 2, 3, 5, 7…………..
• Composite 4, 6, 8, 9…………..
• 1(modulo 4) 1, 5, 9, 13……….…
• 3(modulo 4) 3, 7, 11, 15…………
• Triangular 1, 3, 6, 10……..……
• Perfect 6, 28, 496….……….
• Fibonacci 1, 1, 2, 3, 5, 8….……
3

4.  A number is said to be congruent to 1(modulo 4) if it leaves remainder of 1
when divided by 4 and similarly for 3(modulo 4).
 A number is called triangular if that number of pebbles can be arranged in a
triangle with one pebble at the top, two pebbles in the next row and so on.
 The Fibonacci number are created by starting with 1 and 1.Then to get the
next number in the list, just add the previous two.
 Lastly the number is perfect if the sum of all its divisors, other than itself,
adds back up to the original number. Thus the number dividing 6 are 1, 2
and 3 and 1+2+3=6.
4

5. APPLICATIONS OF NUMBER THEORY
Number theory have countless applications in mathematics as
well as in practical applications including security, memory
management, authentication, coding theory etc. We will examine
a few here.
 Modular Arithmetic
 Congruence and Pseudorandom Number
 Congruence and CRT(Chinese Remainder Theorem)
 Congruence and Cryptography
5

6. MODULAR ARITHMETIC
If ‘a’ and ‘b’ are integers and ‘m’ is a positive integer, then ‘a’ is
congruent to ‘b’ modulo ‘m’, if ‘m‘ divides ‘a-b’.
a ≡ b (mod m)
6

7. Theorem : 1
Let ‘a’ and ‘b’ be integers and let ‘m’ be a positive integer,
Then, a≡b (mod m) iff, a mod m = b mod m
Example : a = 10, b = 26 and m = 8 (10 and 26 are congruent to mod 8)
As, 10 = 1.8 + 2 and 26 = 3.8 +2
Both gives the same remainder 2. So we can write 10 mod 8 = 2 = 26 mod 8.
Theorem : 2
Let ‘m’ be a positive integer.
If, a ≡ b (mod m) and c ≡ d (mod m) Then, a + c ≡ b + d (mod m) and ac ≡ bd (mod m)
Example : Consider 10 ≡ 2 (mod 4) and 12 ≡ 4 (mod 4). Now 10 + 12 =22 and 2 + 4 =6
We find that 22 ≡ 6 (mod 4). Similarly 10.12 ≡ 2.4 (mod 4) i.e 120 ≡ 8 (mod 4).
7

8. Corollary:
Let ‘m’ be a positive integer and let ‘a’ and ‘b’ be integers.
Then, (a + b) mod m ≡ ( (a mod m) + (b mod m) ) mod m
And, ab mod m ≡ ( (a mod m) (b mod m) ) mod m
Proof : We know a ≡ (a mod m) mod m and b ≡ (b mod m) mod m
Then by the previous theorem
a + b ≡ ((a mod m) + (b mod m) ) mod m
ab ≡ ( (a mod m) (b mod m) ) mod m
8

9. CONGRUENCES AND PSEUDORANDOM NUMBERS
• Pseudorandom numbers are the set of values or elements that is statistically
random, but it is derived from a known starting point and is typically
repeated over and over.
• Linear Congruential Generator : A Linear Congruential Generator (LCG) is
an algorithm that yields a sequence of pseudorandom numbers. The method
represents one of the oldest and best known pseudorandom number
generator algorithms.
9

10. Linear Congruence Method:
Choose four integers :
m the modulus
a the multiplier 2 ≤ a < m
c the increment 0 ≤ c < m
x0 the seed 0 ≤ x0< m
Pseudorandom numbers < xn > where n varies 1 to ∞ with 0 ≤ xn ≤ m by using the
congruence xn+1 = ( axn + c ) mod m
• For certain choices of m, a, c, x0 the sequences < xn> becomes periodic.
10

11. Some examples:
Let m = 17, a = 5, c = 2, x0 = 3.
Then the sequence is as follows. xn+1 = ( axn + c) mod m
 x1 = ( ax0 + c) mod m
x1 = ( 5.3 + 2) mod 17
= 17 mod 17 = 0
 x2 = ( ax1 + c) mod m
x2 = ( 5.0 + 2) mod 17
= 2 mod 17 = 2
 x3 = ( ax2 + c) mod m
x3 = ( 5.2 + 2) mod 17
= 12 mod 17 = 12
 x4 = (ax3 + c) mod m
x4 = ( 5.12 + 2 ) mod 17
= 62 mod 17 =11
 x5 = (ax4 + c) mod m
x5 = ( 5.11 + 2) mod 17
= 57 mod 17 = 6
 x6 = ( ax5 + c) mod m
x6 = ( 5.6 + 2) mod 17
= 32 mod 17 = 15 11

12. Euclid’s Algorithm:
It states that if a = bq + r where a, b, q, r ∈ Z
Then, gcd ( a, b) = gcd ( b, r)
Example : Consider finding gcd ( 1768, 184).
Now 1768 = 184 × 9 + 112
So gcd ( 1768 ,184) = gcd (184,112)
= gcd (112,72)
= gcd (72, 40)
= gcd (40, 32)
= gcd (32, 8) = 8
12

13. Extended Euclidean Algorithm:
According to Extended Euclidean algorithm gcd can be expressed as linear
combination of integers.
Theorem :
If ‘a’ and ‘b’ are positive integers, then there exist integers ‘s’ and ‘t’ such that
gcd (a , b) = sa + tb
13

14. Algorithm:
Input : Two positive integers a, b
Output: r = gcd ( a, b) and s, t such that
sa + tb = gcd (a,b)
1. a0 = a, b0 = b
2. t0 = 0, t = 1
3. s0 = 1, s = 0
4. q = [a0 / b0]
5. r = a0 - qb0
6. WHILE r > 0 DO
7. temp = t0 – qt
8. t0 = t, t = temp
9. temp = s0 – qs
10. s0 = s, s = temp
11. a0 = b0, b0 = r
12. q = [a0 / b0], r = a0 - qb0
13. IF r > 0 THEN
14. gcd = r
15. END
16. END
17. Output gcd, s, t 14

15. Example of Extended Euclidean Algorithm:
Therefore, gcd (27,58) = 1 = ( -15).27 + (7).58
= sa + tb
a0 b0 t0 t s0 s q r
27 58 0 1 1 0 0 27
58 27 1 0 0 1 2 4
27 4 0 1 1 -2 6 3
4 3 1 -6 -2 13 1 1
3 1 -6 7 13 -15 3 0
15

16. Euclid’s Algorithm To Compute the Inverse:
Computing the inverse of a modulo m with gcd (a, m) = 1 is to find a−1 such
that a.a−1
≡ 1 (mod m)
Now gcd(a, m) = 1
Hence 1 = sa + tm
Using the EEA, we can find s and t, where sa + tm ≡ sa (mod m), so 1≡ sa
(mod m) which gives s = a−1.
16

17. Example:
Find the inverse of 5 modulo 9?
a = 5 = a0, m = 9 = b0
As, gcd(a, m) = sa + tm
So, gcd (5, 9) = 2.5 + (-1).9 =10 -9 =1
Hence s = 2 is the inverse of a = 5
a0 b0 t0 t s0 s q r
5 9 0 1 1 0 0 5
9 5 1 0 0 1 1 4
5 4 0 1 1 -1 1 1
4 1 1 -1 -1 2 4 0
17

18. CONGRUENCES AND CHINESE REMAINDER THEOREM
A system of linear congruence is simply a set of equivalences over a single variable.
Example : x ≡ 5 (mod 2)
x ≡ 1 (mod 5)
x ≡ 6 (mod 9)
Statement (CRT):
Let m1 ,m2 ,…………,mn be pairwise relatively prime positive integers. The system
x ≡ a1 (mod m1)
x ≡ a2 (mod m2)
. .
. .
. .
x ≡ an (mod mn)
has a unique solution modulo m = m1m2 … … . mn
18

19. Process to solve:
The process by which we can solve the system is as follows.
1. Compute m = m1m2 … … . mn
2. For each k = 1, 2, 3………n compute Mk =
m
mk
.
3. For each k=1, 2, 3………n compute the inverse yk of Mk mod mk.
4. The solution is the sum x = akMkyk
n
k=1 .
19

20. Example:
Q. Give the unique solution to the system
x ≡ 2 (mod 4) x ≡ 1 (mod 5) x ≡ 6 (mod 7) x ≡ 3 (mod 9)
Solution : First calculate m = 4.5.7.9 = 1260 and
M1 =
1260
4
= 315
M2 =
1260
5
= 252
M3 =
1260
7
= 180
M4 =
1260
9
= 140
The inverse of each of these is y1 = 3, y2 = 3 , y3 = 3, y4 = 2. Hence the unique solution is
x = ( a1M1y1 + a2M2y2 + a3M3y3 + a4M4y4 ) mod m
= (2.315.3 + 1.252.3 + 6.180.3 + 3.140.2) mod 1260
= 6726 mod 1260 = 426
Note (How to find Inverse 𝐲 𝐤):
(i) Try every single element ‘a’ , 2≤ a ≤ mk – 1 such that aMk ≡ 1 (mod mk). OR (ii) Use EEA
20

21. LINEAR CONGRUENCE AND CRYPTOGRAPHY
• CRYPTOGRAPHY – the writing and deciphering a secret messages (or
ciphers).
• In the 1980s, a number of cryptographers announced that they had found
methods of writing ciphers in such a way that they could be sent across
public channels while still remaining secrets.
• Those methods are based on the fact that it is relatively easy to raise a prime
number to some exponent but very difficult to find the prime factors of a
large number.
21

22. CIPHER:
• In Cryptography a cipher (cypher) is an algorithm for performing
encryption or decryption i.e. a series of well-defined steps that can be
followed as a procedure to convert information into cipher or code.
1. Caesar Cipher
2. Affine Cipher
3. The RSA Cryptosystem
22

23. CAESAR CIPHER:
• One of the earliest used Cipher in ancient Rome. Also known as a Shift
cipher. It is a substitution cipher where each letter in the original message
(plain text) is replaced with a letter corresponding to a certain number of
letters up or down in the alphabet.
Process:
i. In general first we fix an alphabet, ∈ and let m = |∈|.
ii. Then we fix a secret key, an integer ‘k’ such that 0< k <m. The encryption
and decryption functions are
ek (x) = (x + k) mod m
dk (y) = (y - k) mod m
Note: Cryptographic functions must be one to one.
23

24. Example: Let ∈ = {A,B,C………,Z}. So m = 26. Choose k = 7. Encrypt “HANK” and
decrypt “KLHU” ?
Solution: Denoting A→0, B→1, C→2,…………, Z→25.
HANK can be encoded as (7-0-13-10).
So by Caesar cipher, to encrypt we use
𝐞 𝐤 (x) = (x+k) mod m
e7 (7) = (7+7) mod 26 = 14
e7 (0) = (0+7) mod 26 = 7
e7(13) = (13+7) mod 26 = 20
e7(10) = (10+7) mod 26 = 17
So now encrypted word will be
14→O, 7→H, 20 →U, 17→R
which gives “OHUR”.
“KLHU” is encoded as (10-11-7-20)
To decrypt in Caesar cipher, we use
𝐝 𝐤(y) = (y-k) mod m
d7(10) = (10-7) mod 26 = 3
d7 (11) = (11-7) mod 26 = 4
d7 (7) = (7 -7 ) mod 26 = 0
d7 (20) = (20-7) mod 26 = 13
Now the decrypted cipher becomes
3→D, 4→E, 0→A, 13→N
which gives “DEAN”.
24

25. AFFINE CIPHER:
• Affine cipher is a simple generalisation of Caesar cipher. It operates on each
letter of the plain text by converting them into numbers from 0 to 25.
• If 0 ≤ x ≤ 25 then Encryption and decryption functions are taken as
ek(x) = (ax + b) mod m
dk (y) = a−1 (y – b) mod m
• Here ‘a’ and ‘b’ are integers and only the value of ‘a’ has a restriction since
it has to be co-prime with 26, the possible values could be
a = 1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23 and 25
25

26. It can be encrypted as
(0-19-19-0-2-10) (0-19) (13-14-14-13).
Let’s take a = 3 , b = 7
Now 𝐞 𝐤 (x) = (ax + b) mod 26
ek (0) = (3.0 + 7) mod 26 = 7
ek(19) = (3.19 + 7) mod 26 = 12
ek(19) = (3.19 + 7) mod 26 = 12
ek(0) = (3.0 + 7) mod 26 = 7
ek(2) = (3.2 + 7) mod 26 = 13
ek(10) = (3.10 + 7) mod 26 = 11
ek (0) = (3.0 + 7) mod 26 = 7
ek (19) = (3.19 + 7) mod 26 = 12
ek (13) = (3.13 + 7) mod 26 = 20
ek (14) = (3.14 + 7) mod 26 = 23
ek (14) = (3.14 + 7) mod 26 = 23
ek (13) = (3.13 + 7) mod 26 = 20
(7 -12- 12-7-13-11) - (7-12) -(20-23-23-20)
(h-m-m-h-n-l)–(h-m)–(u-x-x-u)
‘attack at noon’ becomes ‘hmmhnl hm uxxu’
Example: Let the message is “attack at noon”.
Similarly for decryption
𝐃 𝐤(y) = 𝐚−𝟏
(y - b) mod 26
To find a−1
, use ax ≡ 1 (mod 26)
which gives a−1
= 9
Dk(7) = 9 (7-7) mod 26 = 0 mod 26 = 0 = a
Dk(12) = 9 (12-7) mod 26 = 45 mod 26 =19 = t
Dk(12) = 9 (12-7) mod 26 = 45 mod 26 =19 = t
Dk(7) = 9 (7-7) mod 26 = 0 mod 26 = 0 = a
Dk(13) = 9 (13-7) mod 26 = 54 mod 26 = 2 = c
Dk(11) = 9 (11-7) mod 26 = 36 mod 26 = 10 = k
Dk(7) = 9 (7-7) mod 26 = 0 mod 26 = 0 = a
Dk(12) = 9 (12-7) mod 26 = 45 mod 26 = 19 = t
Dk(20) = 9 (20-7) mod 26 = 117 mod 26 = 13 = n
Dk(23) = 9 (23-7) mod 26 = 144 mod 26 = 14 = o
Dk(23) = 9 (23-7) mod 26 = 144 mod 26 = 14 = o
Dk(20) = 9 (20-7) mod 26 = 117 mod 26 = 13 = n
(0-19-19-0-2-10)-(0-19)-(13-14-14-13)
Decrypted message is ‘attack at noon’ 26

27. PUBLIC KEY CRYPTOGRAPHY:
• The problem with Caesar and Affine Cipher is that these two are insecure.
So we still need a secure way to exchange the keys in order to communicate
and for that purpose public key cryptography is used.
• Public key cryptosystem can solve this problem.
1. One can publish a public key.
2. Anyone can encrypt messages.
2. However decryption is done with a private key.
3. The system is secure if no one can feasibly derive the private key
from the public one.
4. It is essential that, encryption should be computationally easy,
while decryption should be computationally hard (without the
private key).
• Mostly used public key cryptography is the RSA cryptosystem.
27

28. THE RSA CRYPTOSYSTEM:
• RSA is one of the first practical public key cryptosystem and is widely used
for secure data transmission.
• In such a cryptosystem, the encryption key is public and differs from the
decryption key which is kept secret.
• RSA is based on the practical difficulty of factoring the product of two large
prime numbers.
• RSA is made of the initial letters of the surnames of Ron Rivest, Adi Shamir
and Leonard Adleman, who first publicly described the algorithm in 1978.
28

29. How RSA Cryptosystem works:
The RSA system works as follows :
i. Choose 2 (large) prime numbers p, q.
ii. Compute n = pq
iii. Compute φ(n) = (p - 1) (q -1)
iv. Choose a, 2 ≤ a ≤ φ (n) such that gcd ( a, φ(n) )=1
v. Compute b = a−1
modulo φ(n)
vi. Note that ‘a’ must be relatively prime to φ(n).
vii. Publish public key (n, a)
viii. Keep private p, q, b and private key is (n, b)
Then the encryption function is simply
ek(x) = xa
mod n
The decryption function is
dk (y) = yb
mod n
Note: b = 𝐚−𝟏
mod 𝛗 (n) can be calculated using EEA. 29

30. Example of RSA:
Alice generates her RSA keys by selecting two primes: p = 11, q = 13.
The modulus n = pq =143
Now φ(n) = (p - 1) (q - 1) = 10 × 12 =120
She chooses 7 for her RSA public key ‘a’
And (7,120) = 1
Now computes her RSA private key using the Extended Euclidean Algorithm as follows.
b= a−1
mod φ (n)
b= 7−1
mod 120 = 103
Now Bob wants to send Alice an encrypted message M, so he obtains her RSA public key (n, a)
Suppose his plain text is just the number 9 and he encrypted into cipher text C as follows:
ek (x) = xa
mod n
ek (9) = 97
mod 143 = 48 = y
When Alice receives Bob’s message she decrypts it by using her RSA private key (b, n) as
follows:
dk (y) = yb
mod n
= 48103
mod 143
= 9 = x
30

31. SUMMARY
• Different type of numbers have been studied under number theory
with their applications.
• Few applications of number theory have been studied such as
Modular Arithmetic
Congruence and Pseudorandom Number
Congruence and CRT(Chinese Remainder Theorem)
Congruence and Cryptography
• All the applications have been studied through examples and have
proved through theorems.
31

32. REFERENCES
[1] Introduction to number theory and its application by Lucia Moura
[2] Number theory applications by Christopher M. Bourke Instructor: Berthe Y. Choueiry
2007
[3] Number theory and computer applications by Ramanujachary Kumanduri
[4] Neal Koblitz. A Course in Number Theory and Cryptography. New York: Springer-
Verlag, 1994
[5] Applications of number theory in cryptography, Zihao Jiang
32

33. THANK YOU
33