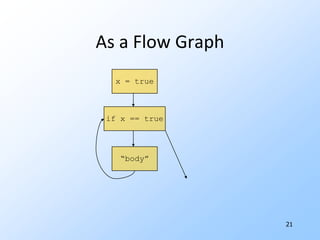
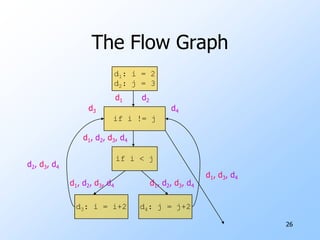
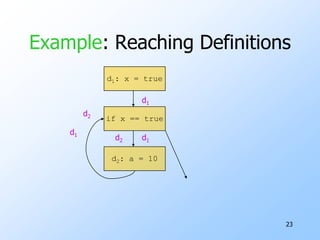
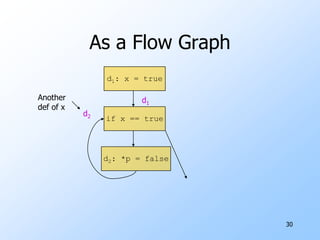
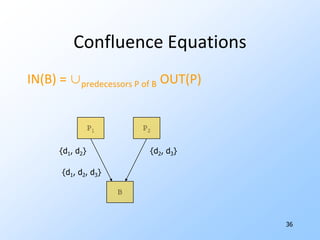
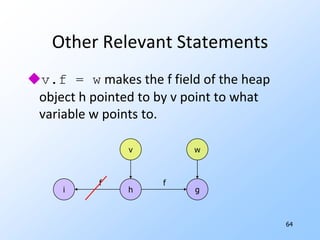
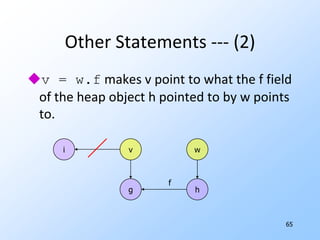
This document provides an introduction and overview of compiler optimization techniques, including: 1) Flow graphs, constant folding, global common subexpressions, induction variables, and reduction in strength. 2) Data-flow analysis basics like reaching definitions, gen/kill frameworks, and solving data-flow equations iteratively. 3) Pointer analysis using Andersen's formulation to model references between local variables and heap objects. Rules are provided to represent points-to relationships.

1. Introduction to CompilersBen LivshitsBased in part of Stanford class slides from http://infolab.stanford.edu/~ullman/dragon/w06/w06.html

2. OrganizationReally basic stuffFlow GraphsConstant FoldingGlobal Common SubexpressionsInduction Variables/Reduction in StrengthData-flow analysisProving Little TheoremsData-Flow EquationsMajor ExamplesPointer analysis

3. Compiler Organization

4. Dataflow Analysis BasicsL2: Compiler OrganizationDataflow analysis basicsL3:Dataflow lattices Integrative dataflow solutionGen/kill frameworks

5. Pointer AnalysisL10:Pointer analysisL11Pointer analysis and bddbddb

6. 6Really Basic StuffFlow Graphs

7. Constant Folding

8. Global Common Subexpressions

9. Induction Variables/Reduction in Strength7Dawn of Code OptimizationA never-published Stanford technical report by Fran Allen in 1968Flow graphs of intermediate codeKey things worth doing

10. 8Intermediate Codefor (i=0; i<n; i++) A[i] = 1;Intermediate code exposes optimizable constructs we cannot see at source-code level.Make flow explicit by breaking into basic blocks = sequences of steps with entry at beginning, exit at end.

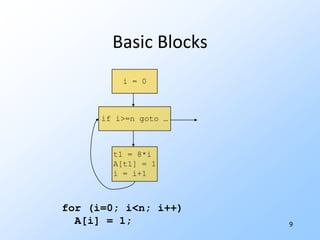
11. 9i = 0if i>=n goto …t1 = 8*i A[t1] = 1i = i+1 Basic Blocks for (i=0; i<n; i++) A[i] = 1;

12. 10Induction Variablesx is an induction variable in a loop if it takes on a linear sequence of values each time through the loop.Common case: loop index like i and computed array index like t1.Eliminate “superfluous” induction variables.Replace multiplication by addition (reduction in strength ).

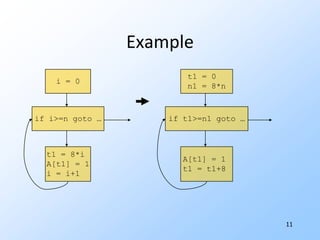
13. 11Examplei = 0if i>=n goto …t1 = 8*i A[t1] = 1i = i+1 t1 = 0 n1 = 8*nif t1>=n1 goto …A[t1] = 1 t1 = t1+8

14. 12Loop-Invariant Code MotionSometimes, a computation is done each time around a loop.Move it before the loop to save n-1 computations.Be careful: could n=0? I.e., the loop is typically executed 0 times.

15. 13Examplei = 0i = 0 t1 = y+zif i>=n goto …if i>=n goto …t1 = y+z x = x+t1 i = i+1 x = x+t1i = i+1

16. 14Constant FoldingSometimes a variable has a known constant value at a point.If so, replacing the variable by the constant simplifies and speeds-up the code.Easy within a basic block; harder across blocks.

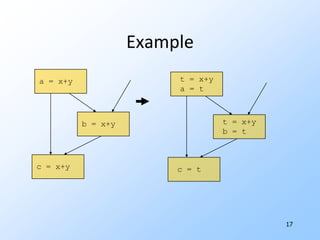
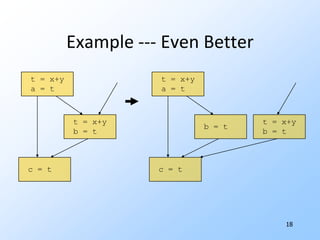
17. 15Examplei = 0 n = 100if i>=n goto …t1 = 8*i A[t1] = 1i = i+1 t1 = 0 if t1>=800 goto …A[t1] = 1 t1 = t1+8

18. 16Global Common SubexpressionsSuppose block B has a computation of x+y.Suppose we are sure that when we reach this computation, we are sure to have:Computed x+y, andNot subsequently reassigned x or y.Then we can hold the value of x+y and use it in B.

19. 17Examplea = x+y t = x+ya = t b = x+y t = x+yb = t c = x+y c = t

20. 18Example --- Even Bettert = x+ya = t t = x+yb = t c = t t = x+ya = t b = t t = x+yb = t c = t

21. 19Data-Flow AnalysisProving Little Theorems

22. Data-Flow Equations

23. Major Examples20An Obvious Theoremboolean x = true;while (x) { . . . // no change to x}Doesn’t terminate.Proof: only assignment to x is at top, so x is always true.

24. 21As a Flow Graphx = trueif x == true“body”

25. 22Formulation: Reaching DefinitionsEach place some variable x is assigned is a definition.Ask: for this use of x, where could x last have been defined.In our example: only at x=true.

26. 23d1d2Example: Reaching Definitionsd1: x = trued1if x == trued2d1d2: a = 10

27. 24ClincherSince at x == true, d1 is the only definition of x that reaches, it must be that x is true at that point.The conditional is not really a conditional and can be replaced by a branch.

28. 25Not Always That Easyint i = 2; int j = 3;while (i != j) { if (i < j) i += 2; else j += 2;}We’ll develop techniques for this problem, but later …

29. 26d1d2d3d4d2, d3, d4d1, d3, d4d1, d2, d3, d4d1, d2, d3, d4The Flow Graphd1: i = 2d2: j = 3if i != jd1, d2, d3, d4if i < jd4: j = j+2d3: i = i+2

30. 27DFA Is Sometimes InsufficientIn this example, i can be defined in two places, and j in two places.No obvious way to discover that i!=j is always true.But OK, because reaching definitions is sufficient to catch most opportunities for constant folding (replacement of a variable by its only possible value).

31. 28Be Conservative!(Code optimization only)It’s OK to discover a subset of the opportunities to make some code-improving transformation.It’s notOK to think you have an opportunity that you don’t really have.

32. 29Example: Be Conservativeboolean x = true;while (x) { . . . *p = false; . . .}Is it possible that p points to x?

33. 30Anotherdef of xd2As a Flow Graphd1: x = trued1if x == trued2: *p = false

34. 31Possible ResolutionJust as data-flow analysis of “reaching definitions” can tell what definitions of x might reach a point, another DFA can eliminate cases where p definitely does not point to x.Example: the only definition of p is p = &y and there is no possibility that y is an alias of x.

35. 32Reaching Definitions FormalizedA definition d of a variable x is said to reach a point p in a flow graph if:Every path from the entry of the flow graph to p has d on the path, andAfter the last occurrence of d there is no possibility that x is redefined.

36. 33Data-Flow Equations --- (1)A basic block can generate a definition.A basic block can eitherKill a definition of x if it surely redefines x.Transmit a definition if it may not redefine the same variable(s) as that definition.

37. 34Data-Flow Equations --- (2)Variables:IN(B) = set of definitions reaching the beginning of block B.OUT(B) = set of definitions reaching the end of B.

38. 35Data-Flow Equations --- (3)Two kinds of equations:Confluence equations : IN(B) in terms of outs of predecessors of B.Transfer equations : OUT(B) in terms of of IN(B) and what goes on in block B.

39. 36Confluence EquationsIN(B) = ∪predecessors P of B OUT(P){d2, d3}{d1, d2}P2P1{d1, d2, d3}B

40. 37Transfer EquationsGenerate a definition in the block if its variable is not definitely rewritten later in the basic block.Kill a definition if its variable is definitely rewritten in the block.An internal definition may be both killed and generated.

41. 38Example: Gen and KillIN = {d2(x), d3(y), d3(z), d5(y), d6(y), d7(z)} d1: y = 3 d2: x = y+zd3: *p = 10d4: y = 5 Kill includes {d1(x), d2(x),d3(y), d5(y), d6(y),…} Gen = {d2(x), d3(x), d3(z),…, d4(y)} OUT = {d2(x), d3(x), d3(z),…, d4(y), d7(z)}

42. 39Transfer Function for a BlockFor any block B:OUT(B) = (IN(B) – Kill(B)) ∪Gen(B)

43. 40Iterative Solution to EquationsFor an n-block flow graph, there are 2n equations in 2n unknowns.Alas, the solution is not unique.Use iterative solution to get the least fixed-point.Identifies any def that might reach a point.

44. 41Iterative Solution --- (2)IN(entry) = ∅;for each block B do OUT(B)= ∅;while (changes occur) do for each block B do {IN(B) = ∪predecessors P of B OUT(P); OUT(B) = (IN(B) – Kill(B)) ∪Gen(B); }

45. 42IN(B1) = {}OUT(B1) = {IN(B2) = {d1,OUT(B2) = {IN(B3) = {d1,OUT(B3) = {Example: Reaching Definitionsd1: x = 5B1d1}d2}if x == 10B2d1,d2}d2}d2: x = 15B3d2}

46. 43Aside: Notice the ConservatismNot only the most conservative assumption about when a def is killed or gen’d.Also the conservative assumption that any path in the flow graph can actually be taken.

47. 44Everything Else About Data Flow AnalysisFlow- and Context-Sensitivity Logical Representation

48. Pointer Analysis

49. Interprocedural Analysis45Three Levels of SensitivityIn DFA so far, we have cared about where in the program we are.Called flow-sensitivity.But we didn’t care how we got there.Called context-sensitivity.We could even care about neither.Example: where could x ever be defined in this program?

50. 46Flow/Context InsensitivityNot so bad when program units are small (few assignments to any variable).Example: Java code often consists of many small methods.Remember: you can distinguish variables by their full name, e.g., class.method.block.identifier.

51. 47Context SensitivityCan distinguish paths to a given point.Example: If we remembered paths, we would not have the problem in the constant-propagation framework where x+y = 5 but neither x nor y is constant over all paths.

52. 48The Example Againx = 3y = 2x = 2y = 3z = x+y

53. 49An Interprocedural Exampleint id(int x) {return x;}void p() {a=2; b=id(a);…}void q() {c=3; d=id(c);…}If we distinguish p calling id from q calling id, then we can discover b=2 and d=3.Otherwise, we think b, d = {2, 3}.

54. 50Context-Sensitivity --- (2)Loops and recursive calls lead to an infinite number of contexts.Generally used only for interprocedural analysis, so forget about loops.Need to collapse strong components of the calling graph to a single group.“Context” becomes the sequence of groups on the calling stack.

55. 51Example: Calling GraphtContexts:GreenGreen, pinkGreen, yellowGreen, pink, yellowsrpqmain

56. 52Comparative ComplexityInsensitive: proportional to size of program (number of variables).Flow-Sensitive: size of program, squared (points times variables).Context-Sensitive: worst-case exponential in program size (acyclic paths through the code).

57. 53Logical RepresentationWe have used a set-theoretic formulation of DFA.IN = set of definitions, e.g.There has been recent success with a logical formulation, involving predicates.Example: Reach(d,x,i) = “definition d of variable x can reach point i.”

58. 54Comparison: Sets Vs. LogicBoth have an efficiency enhancement.Sets: bit vectors and boolean ops.Logic: BDD’s, incremental evaluation.Logic allows integration of different aspects of a flow problem.Think of PRE as an example. We needed 6 stages to compute what we wanted.

59. 55Datalog --- (1)PredicateArguments:variables or constantsThe body :For each assignment of valuesto variables that makes all thesetrue …Make thisatom true(the head ).Atom = Reach(d,x,i)Literal = Atom or NOT AtomRule = Atom :- Literal & … & Literal

60. 56Example: Datalog RulesReach(d,x,j) :- Reach(d,x,i) & StatementAt(i,s) & NOT Assign(s,x) & Follows(i,j)Reach(s,x,j) :- StatementAt(i,s) & Assign(s,x) & Follows(i,j)

61. 57Datalog --- (2)Intuition: subgoals in the body are combined by “and” (strictly speaking: “join”).Intuition: Multiple rules for a predicate (head) are combined by “or.”

62. 58Datalog --- (3)Predicates can be implemented by relations (as in a database).Each tuple, or assignment of values to the arguments, also represents a propositional (boolean) variable.

63. 59Iterative Algorithm for DatalogStart with the EDB predicates = “whatever the code dictates,” and with all IDB predicates empty.Repeatedly examine the bodies of the rules, and see what new IDB facts can be discovered from the EDB and existing IDB facts.

64. 60Example: SeminaivePath(x,y) :- Arc(x,y)Path(x,y) :- Path(x,z) & Path(z,y)NewPath(x,y) = Arc(x,y); Path(x,y) = ∅;while (NewPath != ∅) do { NewPath(x,y) = {(x,y) | NewPath(x,z) && Path(z,y) || Path(x,z) && NewPath(z,y)} – Path(x,y); Path(x,y) = Path(x,y) ∪ NewPath(x,y);}

65. Pointer analysis61

66. 62New Topic: Pointer AnalysisWe shall consider Andersen’s formulation of Java object references.Flow/context insensitive analysis.Cast of characters:Local variables, which point to:Heap objects, which may have fields that are references to other heap objects.

67. 63Representing Heap ObjectsA heap object is named by the statement in which it is created.Note many run-time objects may have the same name.Example: h: T v = new T;says variable v can point to (one of) the heap object(s) created by statement h.vh

68. 64Other Relevant Statementsv.f = w makes the f field of the heap object h pointed to by v point to what variable w points to.fvwfhgi

69. 65Other Statements --- (2)v = w.f makes v point to what the f field of the heap object h pointed to by w points to.vwifhg

70. 66Other Statements --- (3)v = w makes v point to whatever w points to.Interprocedural Analysis : Also models copying an actual parameter to the corresponding formal or return value to a variable.vwh

71. 67Datalog RulesPts(V,H) :- “H: V = new T”Pts(V,H) :- “V=W” & Pts(W,H)Pts(V,H) :- “V=W.F” & Pts(W,G) & Hpts(G,F,H)Hpts(H,F,G) :- “V.F=W” & Pts(V,H) & Pts(W,G)

72. 68ExampleT p(T x) { h: T a = new T; a.f = x; return a;}void main() { g: T b = new T; b = p(b); b = b.f;}