1. The document discusses recursion and provides examples of recursively defined problems and their solutions, including factorials, powers, greatest common divisor, Fibonacci series, Towers of Hanoi, and counting cells in a blob. 2. Recursion involves breaking a problem into smaller subproblems of the same type until reaching a base case that can be solved directly. The solutions to subproblems are then combined to solve the original problem. 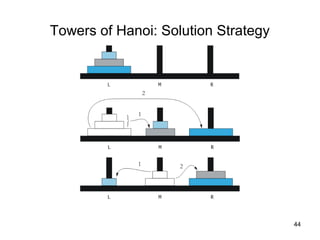3. Examples of recursively defined problems include mathematical formulas, searching and sorting algorithms like binary search, and problems like Towers of Hanoi that are naturally broken down recursively.

1. 1
TDB1023/TCB1063
Recursion

2. 2
Famous Quotations
• To err is human, to forgive divine.
• Alexander Pope, An Essay on Criticism,
English poet and satirist (1688 - 1744)
• To iterate is human, to recurse, divine.
• L. Peter Deutsch, computer scientist, or ....
• Robert Heller, computer scientist, or ....
• unknown ....

3. 3
Outline
• Thinking recursively
• Tracing execution of a recursive method
• Writing recursive algorithms
• Methods for searching arrays
• Solving the Towers of Hanoi problem with recursion
• Processing 2-D images with recursion
• Backtracking to solve search problems, as in mazes

4. 4
Recursive Thinking
• Recursion is:
• A problem-solving approach, that can ...
• Generate simple solutions to ...
• Certain kinds of problems that ...
• Would be difficult to solve in other ways
• Recursion splits a problem:
• Into one or more simpler versions of itself

5. 5
Recursive Thinking: An Example
Strategy for processing nested dolls:
1. if there is only one doll
2. do what it needed for it
else
1. do what is needed for the outer doll
2. Process the inner nest in the same way

6. 6
Recursive Thinking: Another Example
Strategy for searching a sorted array:
1. if the array is empty
2. return -1 as the search result (not present)
3. else if the middle element == target
4. return subscript of the middle element
5. else if target < middle element
6. recursively search elements before middle
7. else
8. recursively search elements after the middle

7. Recursive Thinking: The General Approach
1. if problem is “small enough”
2. solve it directly
3. else
4. break into one or more smaller subproblems
5. solve each subproblem recursively
6. combine results into solution to whole problem
7

8. 8
Requirements for Recursive Solution
• At least one “small” case that you can solve directly
• A way of breaking a larger problem down into:
• One or more smaller subproblems
• Each of the same kind as the original
• A way of combining subproblem results into an
overall solution to the larger problem

9. 9
General Recursive Design Strategy
• Identify the base case(s) (for direct solution)
• Devise a problem splitting strategy
• Subproblems must be smaller
• Subproblems must work towards a base case
• Devise a solution combining strategy

10. 10
Recursive Design Example
Recursive algorithm for finding length of a string:
1. if string is empty (no characters)
2. return 0  base case
3. else  recursive case
4. compute length of string without first character
5. return 1 + that length
Note: Not best technique for this problem; illustrates the approach.

11. 11
Recursive Design Example: Code
Recursive algorithm for finding length of a string:
int size(string str) {
if (str == "")
return 0;
else
return 1 + size(str.substr(1));
}

12. Recursive Design Example: printChars
Recursive algorithm for printing a string:
12
void printChars(string str) {
if (str == "") {
return;
} else {
cout << str.at(0) << endl;
printChars(str.substr(1));
}
}

13. 13
Recursive Design Example:
printCharsReverse
Recursive algorithm for printing a string?
void printCharsReverse(string str) {
if (str == "") {
return;
} else {
printCharsReverse(str.substr(1));
cout << str.at(0) << endl;
}
}

14. Recursive Design Example: mystery
14
What does this do?
int mystery (int n) {
if (n == 0)
return 0;
else
return n + mystery(n-1);
}

15. Proving a Recursive Method Correct
Recall Proof by Induction:
1. Prove the theorem for the base case(s): n=0
2. Show that:
15
• If the theorem is assumed true for n,
• Then it must be true for n+1
Result: Theorem true for all n ≥ 0.

16. Proving a Recursive Method Correct (2)
Recursive proof is similar to induction:
1. Show base case recognized and solved correctly
2. Show that
• If all smaller problems are solved correctly,
• Then original problem is also solved correctly
1. Show that each recursive case makes progress
16
towards the base case  terminates properly

17. 17
Tracing a Recursive Method
length(“ace”)
return 1 + length(“ce”)
return 1 + length(“e”)
return 1 + length(“”)
0
3
2
1
Overall
result

18. 18
Tracing a Recursive Method (2)

19. Recursive Definitions of Mathematical Formulas
• Mathematicians often use recursive definitions
• These lead very naturally to recursive algorithms
• Examples include:
• Factorial
• Powers
• Greatest common divisor
19

20. 20
Recursive Definitions: Factorial
• 0! = 1
• n! = n x (n-1)!
• If a recursive function never reaches its base case, a
stack overflow error occurs

21. 21
int factorial (int n) {
if (n == 0) // or: throw exc. if < 0
return 1;
else
return n * factorial(n-1);
}
Recursive Definitions: Factorial Code

22. 22
Recursive Definitions: Power
• x0 = 1
• xn = x ´ xn-1
double power(double x, int n) {
if (n <= 0) // or: throw exc. if < 0
return 1;
else
return x * power(x, n-1);
}

23. Recursive Definitions: Greatest Common Divisor
Definition of gcd(m, n), for integers m > n > 0:
• gcd(m, n) = n, if n divides m evenly
• gcd(m, n) = gcd(n, m % n), otherwise
int gcd (int m, int n) {
23
if (m < n)
return gcd(n, m);
else if (m % n == 0) // could check n>0
return n;
else
return gcd(n, m % n);
}

24. 24
Recursion Versus Iteration
• Recursion and iteration are similar
• Iteration:
• Loop repetition test determines whether to exit
• Recursion:
• Condition tests for a base case
• Can always write iterative solution to a problem solved
recursively, but:
• Recursive code often simpler than iterative
• Thus easier to write, read, and debug

25. 25
Tail Recursion  Iteration
When recursion involves single call that is at the end ...
It is called tail recursion and it easy to make iterative:
int iterFact (int n) {
int result = 1;
for (int k = 1; k <= n; k++) {
result = result * k;
}
return result;
}

26. 26
Efficiency of Recursion
• Recursive method often slower than iterative; why?
• Overhead for loop repetition smaller than
• Overhead for call and return
• If easier to develop algorithm using recursion,
• Then code it as a recursive method:
• Software engineering benefit probably outweighs ...
• Reduction in efficiency
• Don’t “optimize” prematurely!

27. 27
Recursive Definitions: Fibonacci Series
Definition of fibi, for integer i > 0:
• fib1 = 1
• fib2 = 1
• fibn = fibn-1 + fibn-2, for n > 2

28. 28
Fibonacci Series Code
int fib (int n) {
if (n <= 2)
return 1;
else
return fib(n-1) + fib(n-2);
}
This is straightforward, but an inefficient recursion ...

29. Efficiency of Recursion: Inefficient Fibonacci
29
# calls apparently
O(2n) – big!

30. 30
Efficient Fibonacci
• Strategy: keep track of:
• Current Fibonacci number
• Previous Fibonacci number
• # left to compute

31. 31
Efficient Fibonacci: Code
int fibonacci_start (int n) {
return fibo(1, 0, n);
}
int fibo (
int curr, int prev, int n) {
if (n <= 1)
return curr;
else
return fibo(curr+prev, curr, n-1);
}

32. 32
Efficient Fibonacci: A Trace
Performance is O(n)

33. 33
Recursive Array Search
• Can search an array using recursion
• Simplest way is linear search
• Examine one element at a time
• Start with the first element, end with the last
• One base case for recursive search: empty array
• Result is -1 (negative, not an index  not found)
• Another base case: current element matches target
• Result is index of current element
• Recursive case: search rest, without current element

34. Recursive Array Search: Linear Algorithm
1. if the array is empty
2. return -1
3. else if first element matches target
4. return index of first element
5. else
6. return result of searching rest of the array,
34
excluding the first element

35. 35
Linear Array Search Code
template<typename Item_Type>
int linear_search (
const std::vector<Item_Type>& items,
const Item_Type& target) {
return linear_search(items, target, 0);
}
template<typename Item_Type>
int linear_search (
const std::vector<Item_Type>& items,
const Item_Type& target, size_t pos_first) {
if (pos_first == items.size()) return -1;
else if (target == items[pos_first])
return pos_first;
else
return linear_search(items, target, pos_first+1);
}

36. Array Search: Getting Better Performance
• Item not found: O(n)
• Item found: n/2 on average, still O(n)
• How can we perhaps do better than this?
• What if the array is sorted?
• Can compare with middle item
• Get two subproblems of size £ n/2
• What performance would this have?
• Divide by 2 at each recursion  O(log n)
• Much better!
36

37. 37
Binary Search Algorithm
• Works only on sorted arrays!
• Base cases:
• Empty (sub)array
• Current element matches the target
• Check middle element with the target
• Consider only the array half where target can still lie

38. 38
Binary Search Algorithm Steps
1. if array is empty
2. return -1 as result
3. else if middle element matches
4. return index of middle element as result
5. else if target < middle element
6. return result of searching lower portion of array
7. else
8. return result of searching upper portion of array

39. 39
Binary Search Example

40. 40
Binary Search Code
template <typename Item_Type>
int binary_search(const std::vector<Item_Type>& items,
int first, int last, const Item_Type& target) {
if (first > last)
return -1; // Base case for unsuccessful search.
else {
int middle = (first + last) / 2; // Next probe index.
if (target < items[middle])
return binary_search(items, first, middle - 1, target);
else if (items[middle] < target)
return binary_search(items, middle + 1, last, target);
else
return middle; // Base case for successful search.
}
}

41. 41
Binary Search Code (2)
template <typename Item_Type>
int binary_search(const std::vector<Item_Type>items, const
Item_Type& target) {
return binary_search(items, 0, items.size() - 1, target);
}
• C++ Standard library function binary_search defined
in <algorithms> does this.

42. 42
Problem Solving with Recursion
• Towers of Hanoi
• Counting grid squares in a blob
• Backtracking, as in maze search

43. 43
Towers of Hanoi: Description
Goal: Move entire tower to another peg
Rules:
1. You can move only the top disk from a peg.
2. You can only put a smaller on a larger disk (or
on an empty peg)

44. 44
Towers of Hanoi: Solution Strategy

45. 45
Towers of Hanoi: Solution Strategy (2)

46. 46
Towers of Hanoi: Program Specification
Problem Inputs
Number of disks (an integer)
Letter of starting peg: L (left), M (middle), or R (right)
Letter of destination peg (L, M, or R), but different from starting peg.
Letter of temporary peg (L, M, or R), but different from starting peg and destination peg.
Problem Outputs
A list of moves

47. Towers of Hanoi: Program Specification (2)
47
Function Behavior
void show_moves(int n, char
start_peg, char dest_peg, chat
temp_peg)
Builds a string containing all moves for a
game with n disks on start_peg that will
be moved to dest_peg, using temp_peg
for temporary storage of disks being moved.

48. 48
Towers of Hanoi: Recursion Structure
move(n, src, dst, tmp) =
if n == 1: move disk 1 from src to dst
otherwise:
move(n-1, src, tmp, dst)
move disk n from src to dst
move(n-1, tmp, dst, src)

49. 49
Towers of Hanoi: Code
void show_moves(int n, char start_peg,
char dest_peg, char temp_peg)
{
if (n == 1)
{
cout << "Move disk 1 from peg " << start_peg
<< " to peg " << dest_peg << "n";
}
else
{ // Recursive step
show_moves(n - 1, start_peg, temp_peg, dest_peg);
cout << "Move disk " << n << " from peg " << start_peg
<< " to peg " << dest_peg << "n";
show_moves(n - 1, temp_peg, dest_peg, start_peg);
}
}

50. 50
Towers of Hanoi: Performance Analysis
How big will the output be for a tower of size n?
We’ll just count lines; call this L(n).
• For n = 1, one line: L(1) = 1
• For n > 1, one line plus twice L for next smaller size:
L(n+1) = 2 x L(n) + 1
Solving this gives L(n) = 2n – 1 = O(2n)
So, don’t try this for very large n.

51. 51
Counting Cells in a Blob
• Desire: Process an image presented as a two-dimensional
array of color values
• Information in the image may come from
• X-Ray
• MRI
• Satellite imagery
• Etc.
• Goal: Determine size of any area considered
abnormal because of its color values

52. 52
Counting Cells in a Blob (2)
• A blob is a collection of contiguous cells that are
abnormal
• By contiguous we mean cells that are adjacent,
horizontally, vertically, or diagonally

53. 53
Counting Cells in a Blob: Example

54. Counting Cells in a Blob: Recursive Algorithm
Algorithm count_cells(x, y):
• if (x, y) outside grid
• return 0
• else if color at (x, y) normal
• return 0
• else
• Set color at (x, y) to “Temporary” (normal)
• return 1 + sum of count_cells on neighbors
54

55. 55
Count Cells Code
int count_cells(color grid[ROW_SIZE][COL_SIZE], int r, int c) {
if (r < 0 || r >= ROW_SIZE || c < 0 || c >= COL_SIZE)
{
return 0;
}
else if (grid[r][c] != ABNORMAL)
{
return 0;
}
else
{
grid[r][c] = TEMPORARY;
return 1
+ count_cells(grid, r - 1, c - 1) + count_cells(grid, r - 1, c)
+ count_cells(grid, r - 1, c + 1) + count_cells(grid, r, c + 1)
+ count_cells(grid, r + 1, c + 1) + count_cells(grid, r + 1, c)
+ count_cells(grid, r + 1, c - 1) + count_cells(grid, r, c - 1);
}
}

56. 56
Backtracking
• Backtracking: systematic trial and error search for
solution to a problem
• Example: Finding a path through a maze
• In walking through a maze, probably walk a path as far
as you can go
• Eventually, reach destination or dead end
• If dead end, must retrace your steps
• Loops: stop when reach place you’ve been before
• Backtracking systematically tries alternative paths and
eliminates them if they don’t work

57. 57
Backtracking (2)
• If you never try exact same path more than once, and
• You try all possibilities,
• You will eventually find a solution path if one exists
• Problems solved by backtracking: a set of choices
• Recursion implements backtracking straightforwardly
• Activation frame remembers choice made at that
decision point
• A chess playing program likely involves backtracking

58. 58
Maze Solving Algorithm: findPath(x, y)
1. if (x,y) outside grid, return false
2. if (x,y) barrier or visited, return false
3. if (x,y) is maze exit, color PATH and return true
4. else:
5. set (x,y) color to PATH (“optimistically”)
6. for each neighbor of (x,y)
7. if findPath(neighbor), return true
8. set (x,y) color to TEMPORARY (“visited”)
9. return false

59. 59
Maze Solving Code
bool findMazePath(color grid[ROW_SIZE][COL_SIZE], int r, int c)
{
if (r < 0 || c < 0 || r >= ROW_SIZE || c >= COL_SIZE)
return false; // Cell is out of bounds.
else if (grid[r][c] != BACKGROUND)
return false; // Cell is on barrier or dead end.
else if (r == ROW_SIZE - 1 && c == COL_SIZE - 1)
{
grid[r][c] = PATH; // Cell is on path
return true; // and is maze exit.
}
else
. . .
}

60. 60
Maze Solving Code (2)
{ // Recursive case.
// Attempt to find a path from each neighbor.
// Tentatively mark cell as on path.
grid[r][c] = PATH;
if (findMazePath(grid, r - 1, c)
|| findMazePath(grid, r + 1, c)
|| findMazePath(grid, r, c - 1)
|| findMazePath(grid, r, c + 1 ) )
{
return true;
}
else
{
grid[r][c] = TEMPORARY; // Dead end.
return false;
}
}