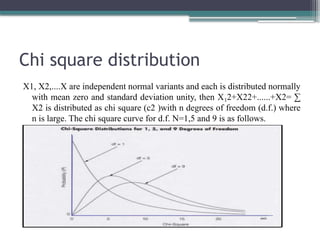
The document provides an overview of parametric and non-parametric statistical tests, outlining their definitions, assumptions, advantages, and disadvantages. It discusses various tests such as the Wilcoxon rank test, Chi-square test, and their applications in hypothesis testing. Additionally, it highlights the conditions under which non-parametric tests are preferred over parametric tests.

1. Non- Parametric Test
Wilcoxan Rank Test, Analysis of variance,
Correlation, Chi square test
Submitted To-
Dr. Rameshwar Dass
(Associate Professor)
Submitted By-
Muskan (M.Pharm)
3rd
Semester
GURU GOBIND SINGH COLLEGE OF PHARMACY

2. Contents
• Introduction
• Difference between parametric & non-parametric tests
• Advantages and Disadvantages of Non-Parametric tests
• Hypothesis
• Different Parametric Tests
• Wilcoxan Rank Test
• Analysis of variance
• Correlation
• Chi square test

3. Introduction
• Parametric Tests:- If the information about the population is completely known by means
of its parameters then statistical test is called parametric test.
• Parametric tests are restricted to data that:
• show a normal distribution
• are independent of one another
• are on the same continuous scale of measurement
• Non-Parametric Tests :- If there is no information about the population but still it is
required to test the hypothesis of the population, then statistical test is called non-parametric
tests.
• Non-Parametric tests are restricted to data that:
• show an other than normal distribution
• are dependent or conditional on one another
• in general, do not have a continuous scale of measurement
• For example, The height and weight of something > Parametric Vs. Did the bacteria grow or
not > Non-Parametric

4. Introduction
• Parametric Tests :- Parametric tests are normally involve to data expressed in
absolute numbers or values rather than ranks; an example is the Student's t-test.
• The results of a parametric test depends on the validity of the assumption.
• Parametric tests are most powerful for testing the significance.
• Non-Parametric Tests :- Where we can not use the assumptions & conditions of
parametric statistical procedures, in such situation we apply non-parametric tests.
• It covers the data techniques that do not rely on data belonging to any particular
distribution.
• In this statistics is based on the ranks of observations and do not depend on any
distribution of the population.
• In non-parametric statistics, the techniques do not assume that the structure of a
model is fixed.
• It deals with small sample sizes, and, these are user friendly compared with
parametric statistics and economical in time.

5. Difference Between Parametric and Non-
Parametric Test
Parametric tests Non-parametric tests
It makes assumptions about the
parameters of the population
distribution(s) from which one's data are
drawn
It makes no such assumptions
The information about the population is
completely known by means of its
parameters
There is no information about the
population but still it is required to test the
hypothesis of the population,
The data should be normally distributed Data does not follow any specific
distribution, So, it is known as
"distribution free tests"
Null hypothesis is made on parameters of
the population distribution
The null hypothesis is free from
parameters
It is applicable only for variable It is applicable for both variables and
attributes

6. Advantages of Non- Parametric Test
• Non-parametric tests are simple and easy to understand
• It will not involve complicated sampling theory
• No assumption is made regarding the parent population
• Non-parametric test just need nominal or ordinal data
• It is easy to applicable for attribute dates
• Non-parametric statistics are more versatile tests
• Easier to calculate
• The hypothesis tested by the non-parametric test may be more appropriate

7. Disadvantages of Non Parametric Test
• Non-parametric methods are not so efficient as of parametric test
• No nonparametric test available for testing the interaction in ANOVA
model
• Tables necessary to implement non-parametric tests which are scattered
widely and appear in different formats
• Require a larger sample size than corresponding parametric test in order to
achieve same power
• Difficult to compute for large samples
• Start Stat tables are not readily available

8. Hypothesis
• HYPOTHESIS
• NULL HYPOTHESIS: (H) states that no association exists between the
two cross-tabulated variables in the population, and therefore the variables
are statistically independent. E.g. if we want to compare 2 methods method
A and method B for its superiority, and if the assumption is that both
methods are equally good, then this assumption is called as NULL
HYPOTHESIS.
• ALTERNATIVE HYPOTHESIS: (H) proposes that the two variables are
related in the population. If we assume that from 2 methods, method A is
superior than method B, then this assumption is called as ALTERNATIVE
HYPOTHESIS

9. Chi- Square Test
• The chi-square test is an important test amongst the several tests of
significance developed by statisticians.
• It was developed by Karl Pearson in1900.
• CHI SQUARE TEST is a non parametric test not based on any
assumption or distribution of any variable.
• This statistical test follows a specific distribution known as chi square
distribution.
• In general the test used to measure the differences between what is
observed and what is expected according to an assumed hypothesis is
called the chi-square test.
• The entire large sample theory was based on the application of "Normality
test".

10. Calculation of chi square test
Where, O observed frequency
E = expected frequency
If two distributions (observed and theoretical) are
exactly alike, x2= 0; (but generally due to
sampling errors, x2 is not equal to zero)

11. Applications of Chi-Square test
• Hypothesis testing procedures of chi-square test are:
• Tests for proportions
• Tests of Association
• Tests of Goodness-of-fit.
• It can also be used when more than two groups are to be compared.
• h x k contingency table. (h = No. of Rows, k = No. of Columns)

12. STEPS FOR CALCULATION OF CHI-SQUARE
TEST PROCEDURE
(i) Calculate the expected frequencies and the observed frequencies:
Expected frequencies f: the cell frequencies that would be expected in a
contingency table if the two variables were statistically independent.
Observed frequencies f o: the cell frequencies actually observed in a
contingency table.
(ii) f = (column total) (row total)/ N
(iii) To obtain the expected frequencies for any cell in any cross- tabulation
in which the two variables are assumed independent, multiply the row
and column totals for that cell and divide the product by the total
number of cases in the table

13. STEPS FOR CALCULATION OF CHI-SQUARE
TEST PROCEDURE
iv.

14. Chi square distribution
X1, X2,....X are independent normal variants and each is distributed normally
with mean zero and standard deviation unity, then X 2+Χ22+......+Χ2= ∑
₁
X2 is distributed as chi square (c2 )with n degrees of freedom (d.f.) where
n is large. The chi square curve for d.f. N=1,5 and 9 is as follows.

15. • DEGREE OF FREEDOM: It denotes the extent of independence
(freedom) enjoyed by a given set of observed frequencies
• d.f. = (number of frequencies) - (number of independent constraints )
• In other terms, d.f.= (r-1)(c-1) where r = the number of rows c = the
number of columns
• If degree of freedom > 2: Distribution is bell shaped
• If degree of freedom = 2: Distribution is L shaped with maximum
ordinate at zero
• If degree of freedom <2 (>0): Distribution L shaped with infinite
ordinate at the origin.

17. Sign Test
• The sign test is used to compare the continuous outcome in the
paired samples or the two matches samples.
• Null hypothesis, H0: Median difference should be zero
• Test statistic: The test statistic of the sign test is the smaller of the
number of positive or negative signs.
• Decision Rule: Reject the null hypothesis if the smaller of number
of the positive or the negative signs are less than or equal to the
critical value from the table.

18. WILCOXON SIGNED-RANK TEST
• Wilcoxon signed-rank test is used to compare the continuous
outcome in the two matched samples or the paired samples.
• Null hypothesis, H0: Median difference should be zero.
• Test statistic: The test statistic W, is defined as the smaller of W+
or W- .
• Where W+ and W- are the sums of the positive and the negative
ranks of the different scores.
• Decision Rule: Reject the null hypothesis if the test statistic, W is
less than or equal to the critical value .

19. Wilcoxan Rank sum Test
• Mann Whitney U test is used to compare the continuous outcomes in the
two independent samples.
• Null hypothesis, H0: The two populations should be equal.
• Test statistic:
• If R1 and R2 are the sum of the ranks in group 1 and group 2 respectively,
then the test statistic “U” is the smaller of:
• U1=n1n2+n1(n1+1)/2−R1
• U2=n1n2+n2(n2+1)/2−R2
• Decision Rule: Reject the null hypothesis if the test statistic, U is less than
or equal to critical value.

20. Kruskal Wallis test- Analysis of variance by
ranks
• Kruskal Wallis test is used to compare the continuous outcome in greater than two
independent samples.
• Null hypothesis, H0: K Population medians are equal.
• Test statistic:
• If N is the total sample size, k is the number of comparison groups, Rj is the sum of the
ranks in the jth group and nj is the sample size in the jth group, then the test statistic, H is
given by:
• Decision Rule: Reject the null hypothesis H0 if H ≥ critical value

21. Friedman Test
• Friedman Test: It is a non-parametric test alternative to the one way
ANOVA with repeated measures. It tries to determine if subjects changed
significantly across occasions/conditions.
• Elements of Friedman Test
• One group that is measured on three or
more blocks of measures overtime/experimental conditions.
• One dependent variable which can be Ordinal, Interval or Ratio.
• Assumptions of Friedman Test
• The group is a random sample from the population.
• Samples are not normally distributed.

22. Friedman Test
• Null and Alternate Hypothesis of Friedman Test
• Null Hypothesis: There is no significant difference between the given conditions of
measurement OR the probability distributions for all the conditions are the same.
(Medians are same)
• Alternate Hypothesis: At least 2 of them differ from each other
• Test Statistic for Friedman Test
• Fr=
• n = total number of subjects/participants.
• k = total number of blocks to be measured.
• Ri = sum of ranks of all subjects for a block I
• If FR is greater than the critical value limits reject the Null Hypothesis. Otherwise, accept
the Null Hypothesis.

23. Spearman correlation
• Spearman correlation is a non-parametric test that is used to measure the
degree and direction of the relationship between two variables. The
Spearman correlation is the appropriate correlation analysis when the
variables are measured on a scale or ordinal
• Characteristics Spearman Correlation :
- it assigns a value between − 1 and 1
- 0 is no correlation between ranks
- 1 is total positive correlation between ranks, — 1 is total negative
correlation between ranks

24. • Correlation hypothesis :
assumes that there is a correlation between ranks
Ho: There is no correlation between ranks
Ha: There is correlation between ranks
• When your p-value is less than or equal to your significance level
(0.05), you reject the null hypothesis

25. Applications of Non Parametric Test
• The conditions when non-parametric tests are used are listed below:
• When parametric tests are not satisfied.
• When testing the hypothesis, it does not have any distribution.
• For quick data analysis.
• When unscaled data is available.

26. THANKYOU