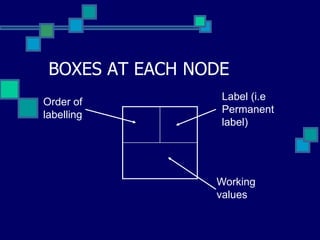
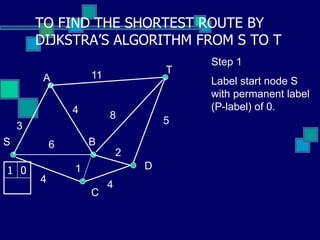
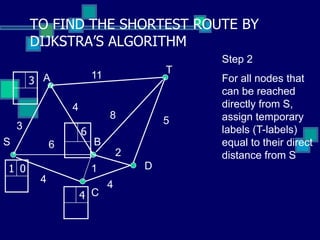
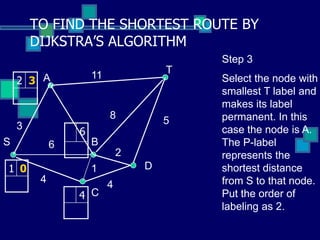
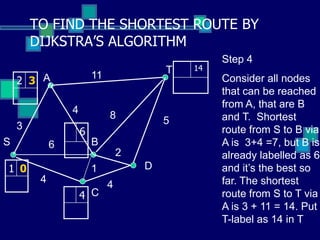
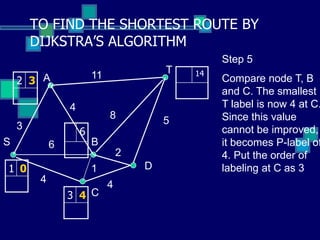
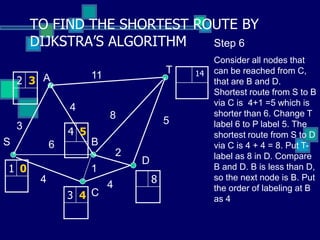
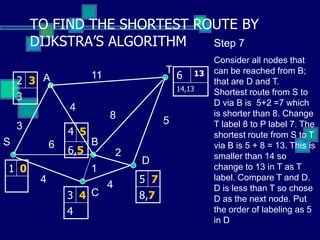
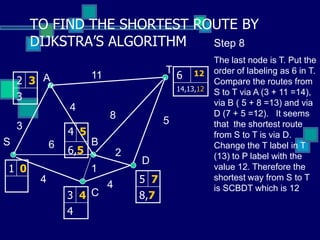
This document describes Dijkstra's algorithm, a greedy algorithm used to find the shortest paths between nodes in a graph. It explains that Dijkstra's algorithm works by assigning permanent labels to nodes starting with the source node, then iteratively assigning temporary labels to neighboring nodes to track the shortest path distances from the source. The algorithm is demonstrated on a sample graph with 6 nodes labeled A through T, showing how it progressively assigns labels to nodes in order to find the shortest path from node S to node T.

1. DIJKSTRA'S ALGORITHM,
BY
DR HJH RAHMAH BT MURSHIDI

2. INTRODUCTION
 Dijkstra's algorithm, named after its
discoverer, Dutch computer scientist Edsger
Dijkstra
 A greedy algorithm that solves the single-source
shortest path problem for a directed graph with
non negative edge weights.

3. INTRODUCTION
 For example, if the vertices of the graph
represent cities and edge weights represent
driving distances between pairs of cities
connected by a direct road, Dijkstra's algorithm
can be used to find the shortest route between
two cities.

4.  The input of the algorithm consists of a weighted
directed graph G and a source vertex s in G
 Denote V as the set of all vertices in the graph G.
 Each edge of the graph is an ordered pair of
vertices (u,v)
 This representings a connection from vertex u to
vertex v

5.  The set of all edges is denoted E
 Weights of edges are given by a weight function
w: E → [0, ∞)
 Therefore w(u,v) is the cost of moving directly
from vertex u to vertex v
 The cost of an edge can be thought of as (a
generalization of) the distance between those
two vertices

6.  The cost of a path between two vertices is the
sum of costs of the edges in that path
 For a given pair of vertices s and t in V, the
algorithm finds the path from s to t with lowest
cost (i.e. the shortest path)
 It can also be used for finding costs of shortest
paths from a single vertex s to all other vertices
in the graph.

7. BOXES AT EACH NODE
Order of
labelling
Label (i.e
Permanent
label)
Working
values

8. TO FIND THE SHORTEST ROUTE BY
DIJKSTRA’S ALGORITHM FROM S TO T
S
A
B
T
D
C
3
11
5
8
6
4
1
2
4
Step 1
Label start node S
with permanent label
(P-label) of 0.
1 0
4

9. TO FIND THE SHORTEST ROUTE BY
DIJKSTRA’S ALGORITHM
4
3
1 0
S
A
B
T
D
C
3
11
5
8
6
4
1
2
4
Step 2
For all nodes that
can be reached
directly from S,
assign temporary
labels (T-labels)
equal to their direct
distance from S
6
4

10. TO FIND THE SHORTEST ROUTE BY
DIJKSTRA’S ALGORITHM
4
2 3
1 0
S
A
B
T
D
C
3
11
5
8
6
4
1
2
4
Step 3
Select the node with
smallest T label and
makes its label
permanent. In this
case the node is A.
The P-label
represents the
shortest distance
from S to that node.
Put the order of
labeling as 2.
6

11. TO FIND THE SHORTEST ROUTE BY
DIJKSTRA’S ALGORITHM
4
2 3
1 0
S
A
B
T
D
C
3
11
5
8
6
4
1
2
4
Step 4
Consider all nodes
that can be reached
from A, that are B
and T. Shortest
route from S to B via
A is 3+4 =7, but B is
already labelled as 6
and it’s the best so
far. The shortest
route from S to T via
A is 3 + 11 = 14. Put
T-label as 14 in T
6
4
14

12. TO FIND THE SHORTEST ROUTE BY
DIJKSTRA’S ALGORITHM
3 4
2 3
1 0
S
A
B
T
D
C
3
11
5
8
6
4
1
2
4
Step 5
Compare node T, B
and C. The smallest
T label is now 4 at C.
Since this value
cannot be improved,
it becomes P-label of
4. Put the order of
labeling at C as 3
6
4
14

13. TO FIND THE SHORTEST ROUTE BY
DIJKSTRA’S ALGORITHM
3 4
2 3
1 0
S
A
B
T
D
C
3
11
5
8
6
4
1
2
4
Step 6
Consider all nodes that
can be reached from C,
that are B and D.
Shortest route from S to B
via C is 4+1 =5 which is
shorter than 6. Change T
label 6 to P label 5. The
shortest route from S to D
via C is 4 + 4 = 8. Put T-
label as 8 in D. Compare
B and D. B is less than D,
so the next node is B. Put
the order of labeling at B
as 4
4 5
4
14
8

14. TO FIND THE SHORTEST ROUTE BY
DIJKSTRA’S ALGORITHM
3 4
4
2 3
3
1 0
S
A
B
T
D
C
3
11
5
8
6
4
1
2
4
Step 7
Consider all nodes that
can be reached from B;
that are D and T.
Shortest route from S to
D via B is 5+2 =7 which
is shorter than 8. Change
T label 8 to P label 7. The
shortest route from S to T
via B is 5 + 8 = 13. This is
smaller than 14 so
change to 13 in T as T
label. Compare T and D.
D is less than T so chose
D as the next node. Put
the order of labeling as 5
in D
4 5
6,5
4
6 13
14,13
5 7
8,7

15. TO FIND THE SHORTEST ROUTE BY
DIJKSTRA’S ALGORITHM
3 4
4
2 3
3
1 0
S
A
B
T
D
C
3
11
5
8
6
4
1
2
4
Step 8
The last node is T. Put the
order of labeling as 6 in T.
Compare the routes from
S to T via A (3 + 11 =14),
via B ( 5 + 8 =13) and via
D (7 + 5 =12). It seems
that the shortest route
from S to T is via D.
Change the T label in T
(13) to P label with the
value 12. Therefore the
shortest way from S to T
is SCBDT which is 12
4 5
6,5
4
6 12
14,13,12
5 7
8,7