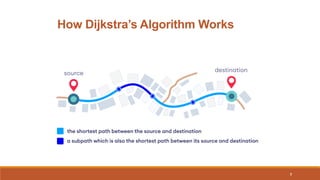
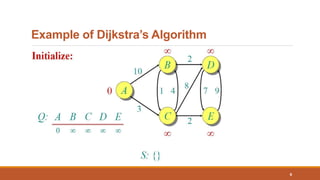
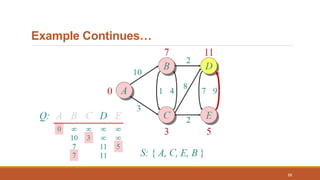
The document presents Dijkstra’s shortest path algorithm, developed by Edsger W. Dijkstra in 1956, which solves the single source shortest path problem in both directed and undirected graphs. It outlines the algorithm's complexity, advantages, and disadvantages, as well as its applications in fields like digital mapping and network routing. Additionally, the document includes detailed examples and pseudocode to illustrate how the algorithm operates.

1. Dijkstra’s Shortest Path Algorithm
Presented By:
Tamzida Azad
ID: …………..
Section: …………..
Presented To:
Dr. Selina Sharmin
Associate Professor
Department of Computer Science & Engineering

2. Table of Contents
2
Serial Topic Slide Number
1 Creator of Dijkstra Algorithm 3
2 What is Dijkstra’s Algorithm? 4
4 Dijkstra’s Algorithm 5
5 Pseudo Code 6
6 How Dijkstra’s Algorithm Works? 7
7 Example 8-13
8 Example 14-17
9 Dijkstra’s Algorithm Complexity 20
10 Application of Dijkstra’s Algorithm 21-23
11 Different Shortest Path Algorithm’s Complexity Analysis 24
12 Advantage & Disadvantage of Dijkstra’s Algorithm 25
13 Q/A session 26

3. Creator of Dijkstra’s Algorithm
 Designed by Dutch physicist Edsger Wybe Dijkstra in 1956
 Received Turing award in 1972 for fundamental contributions to programming
as a high, intellectual challenge
 The Edsger W. Dijkstra Paper Prize in Distributed Computing is given for outstanding papers
on the principles of distributed computing
 Famous Quote:
“Computer Science is no more about computers than astronomy is about telescopes."
3
Edsger Wybe Dijkstra

4. Why Dijkstra’s Algorithm?
 Used to solve the single source shortest path problem
 Finds the shortest distance between two vertices on a graph
 Creates tree of shortest paths from starting source vertex to all other points in the graph
 Works on both directed and undirected graphs
 Differs from minimum spanning tree
 Similar to BFS
 Gives optimal solution using greedy method
4

5. Dijkstra’s Algorithm
 Approach: Greedy
 Input: Weighted graph G={E,V} and source vertex v∈V, such that all edge weights are
nonnegative
 Output: Lengths of shortest paths (or the shortest paths themselves) from a given source
vertex v∈V to all other vertices
5

6. 6
Dijkstra’s Algorithm Pseudo Code

7. 7
How Dijkstra’s Algorithm Works

8. Example of Dijkstra’s Algorithm
8

9. Example Continues…
9

10. Example Continues…
10

11. Example Continues…
11

12. Example Continues…
12

13. Example Continues…
13

14. Example Continues…
14

15. Example Continues…
15

16. Example Continues…
16

17. Example Continues…
17

18. Dijkstra's Algorithm Complexity
 Time Complexity: O(𝑉2
)
With min priority queue time complexity is O(V + E Log V)
E = Number of edges and
V = Number of vertices
 Space Complexity: O(V)
18

19. 19

20. Digital Mapping Services in Google Maps
 Used to find the minimum distance between two
locations along the path.
 Example:
Finding shortest route between Uttara to
Mohammadpur using Google Map.
20

21. Social Networking Applications
 Apps suggesting friends to connect
 Uses the shortest path between users measured
through handshakes or connections among them.
21

22. Telephone Network
 Used in network bandwidth measurement
 If a city is a graph, the vertices represent the
switching stations, and the edges represent the
transmission lines.
22

23. IP routing
 Finds the best path between the source and the
destination router
 Used to update forwarding table
 Provides the shortest cost path from the source
router to other routers
23

24. 24
Comparing Complexity of Different Shortest Path Algorithm

25. Advantage and Disadvantage of Dijkstra’s Algorithm
Advantage
 O(𝑛2
) so efficient enough to use for relatively
large problems
 Used enormously in Google Map, IP routing,
robotic path detection, file server etc
 Low complexity, optimal and uniform
 Almost linear and works for both directed &
undirected graph.
Disadvantage
 Consume time by doing blind search
 Can not handle negative edges
 Leads to acyclic graphs
25

26. Any Question

27. 27