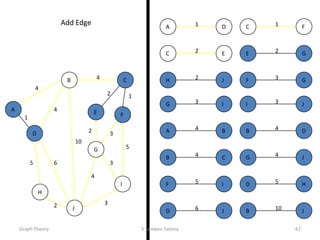
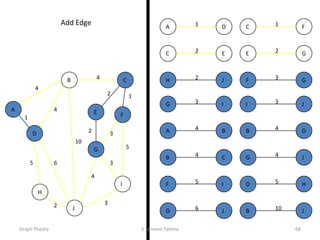
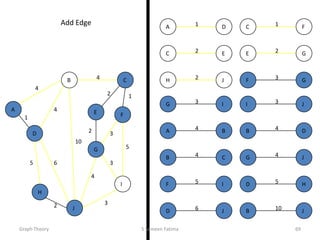
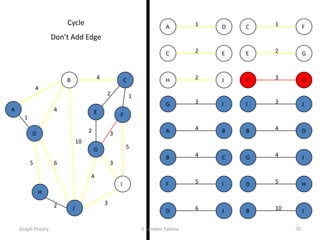
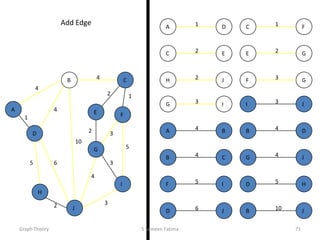
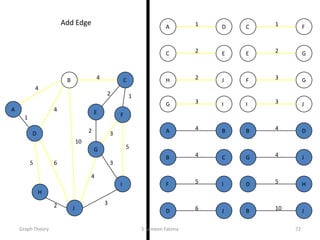
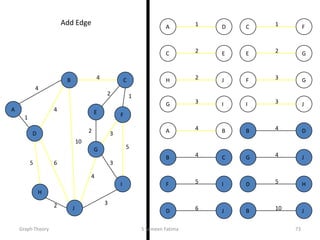
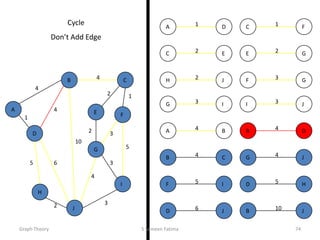
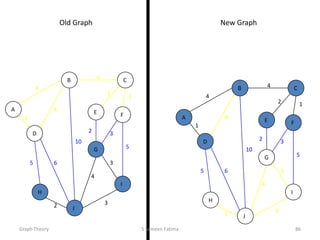
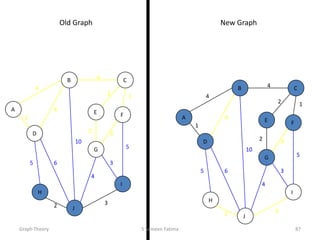
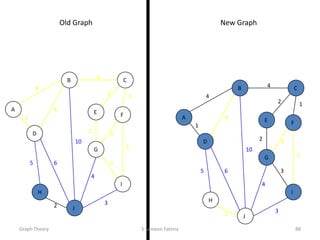
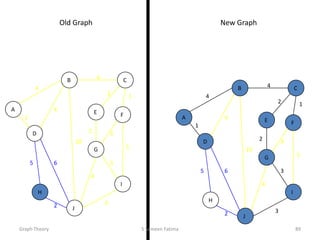
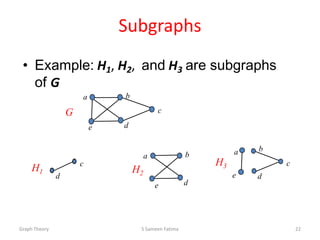
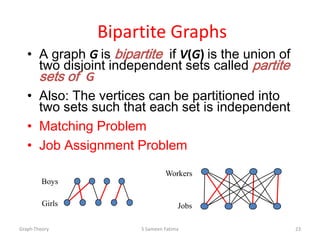
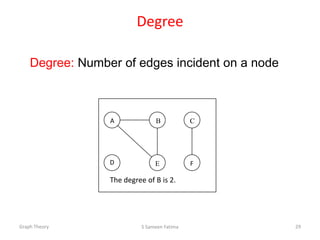
This document provides an overview of graph theory concepts including:
- The basics of graphs including definitions of vertices, edges, paths, cycles, and graph representations like adjacency matrices.
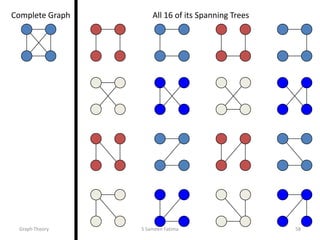
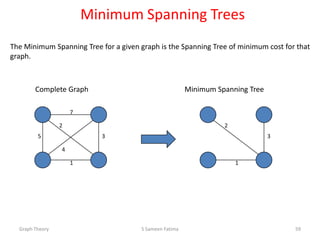
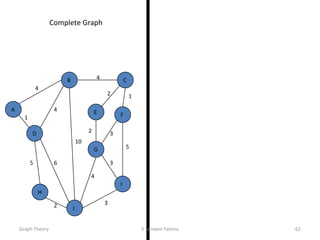
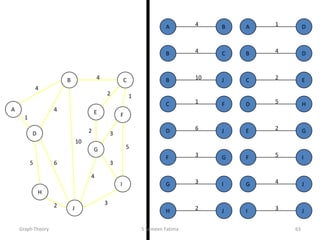
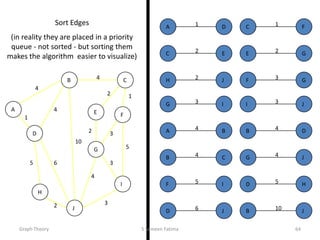
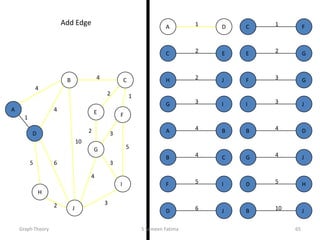
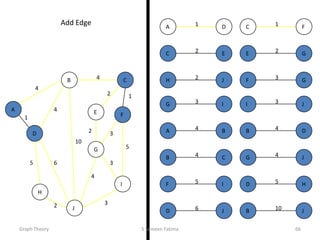
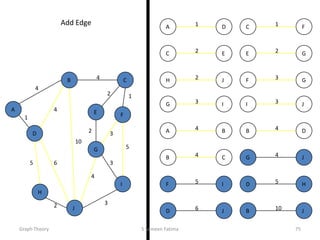
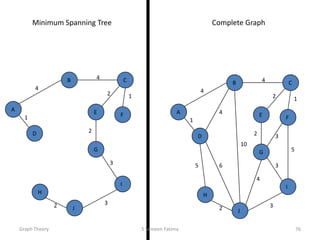
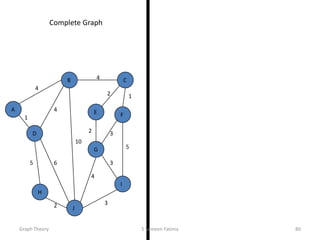
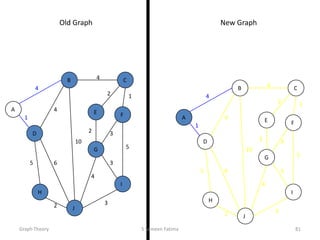
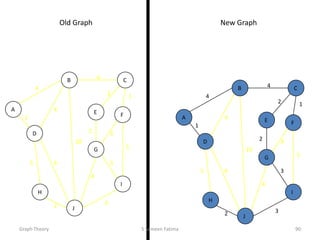
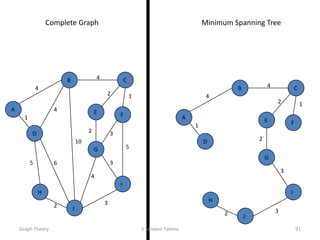
- Minimum spanning tree algorithms like Kruskal's and Prim's which find a spanning tree with minimum total edge weight.
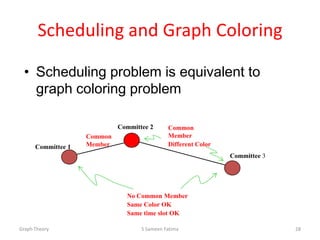
- Graph coloring problems and their applications to scheduling problems.
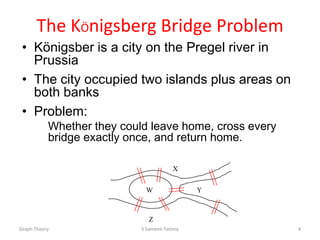
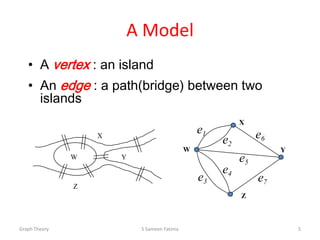
- Other graph concepts covered include degree, Eulerian paths, planar graphs and graph isomorphism.



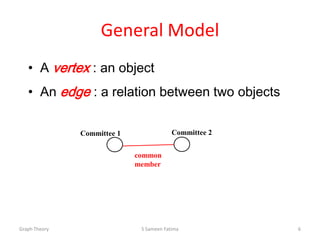
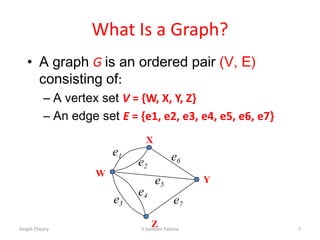


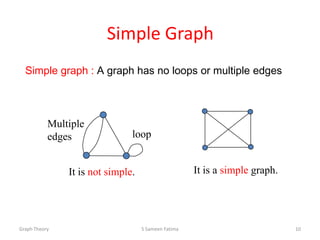


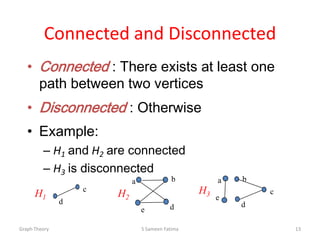
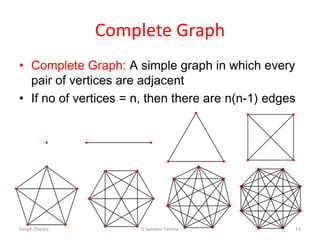

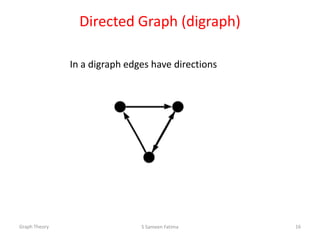
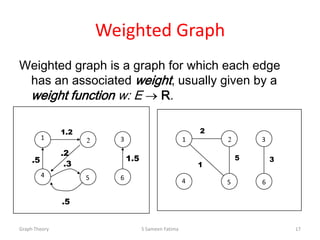
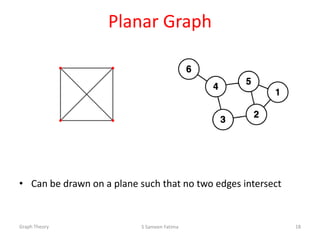








![Path
• A path is a sequence of vertices such that there is
an edge from each vertex to its successor.
• A path is simple if each vertex is distinct.
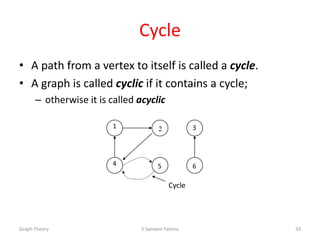
• A circuit is a path in which the terminal vertex
coincides with the initial vertex
Graph Theory S Sameen Fatima 32
1 2 3
4 5 6
Simple path: [ 1, 2, 4, 5 ]
Path: [ 1, 2, 4, 5, 4]
Circuit: [ 1, 2, 4, 5, 4, 1]](https://image.slidesharecdn.com/vignan-130911102520-phpapp01/85/graph-theory-31-320.jpg)






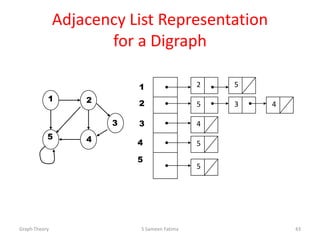
![Adjacency List Representation
• Adjacency-list representation
– an array of |V | elements, one for each vertex in V
– For each u V , ADJ [ u ] points to all its adjacent
vertices.
Graph Theory S Sameen Fatima 42](https://image.slidesharecdn.com/vignan-130911102520-phpapp01/85/graph-theory-41-320.jpg)