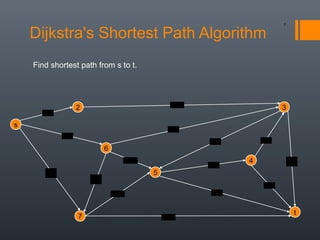
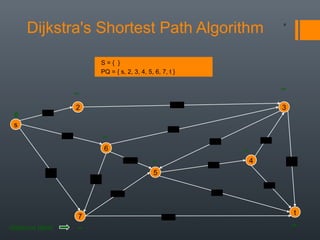
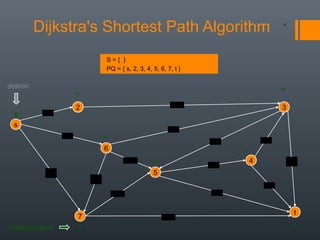
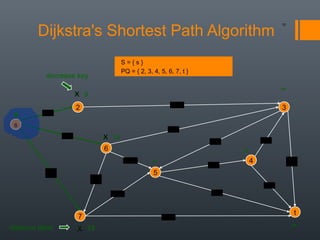
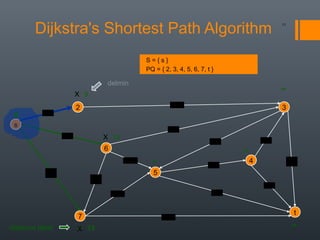
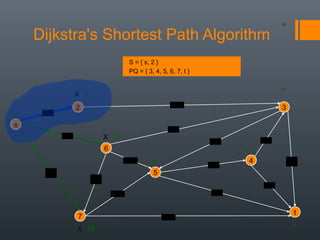
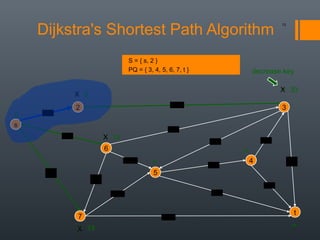
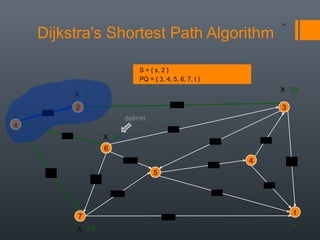
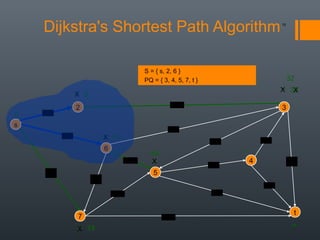
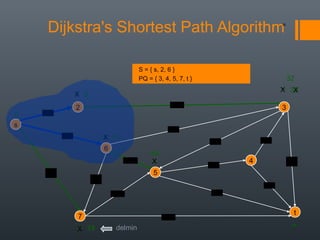
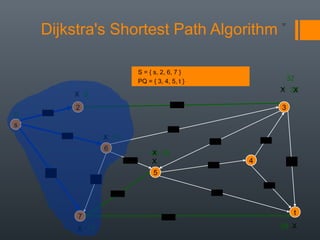
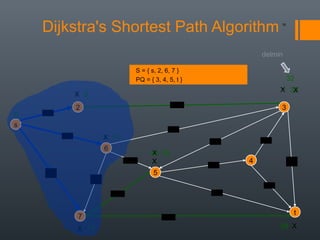
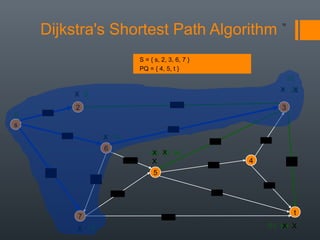
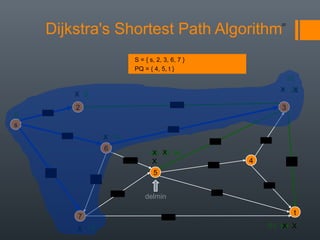
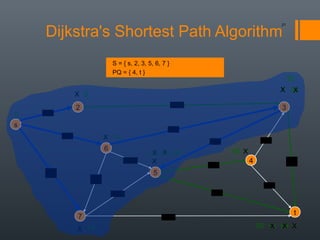
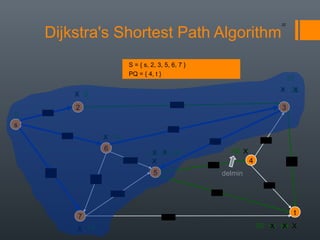
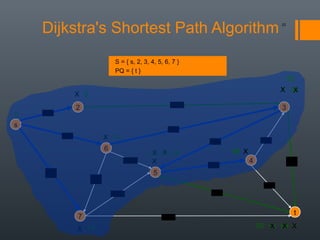
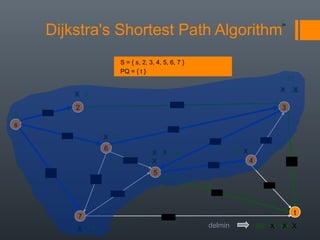
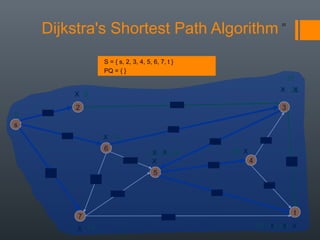
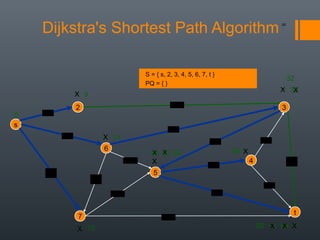
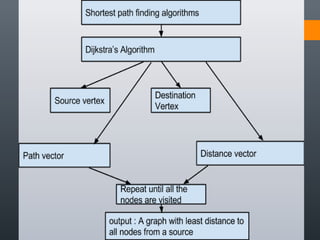
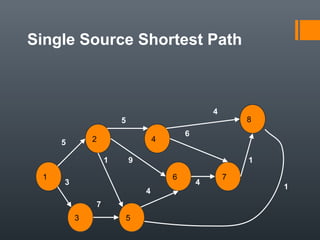
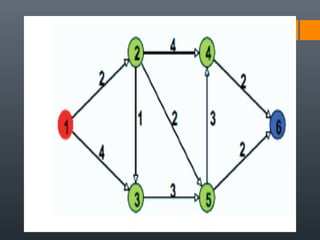
Dijkstra's algorithm is used to find the shortest path between a starting vertex and any other vertex in a graph with positive edge weights. It works by maintaining a distance label for each vertex, with the starting vertex's label set to 0. It then iteratively selects the unprocessed vertex with the smallest distance label and relaxes any incident edges that improve neighboring vertices' distance labels, until all vertices have been processed. Storing predecessor vertices allows reconstruction of the shortest path.

1. .Shortest Path Problems
- Greedy Approach

2. INTRODUCTION
Dijkstra’s algorithm calculates the least distance
from a starting vertex to a destination vertex from
the given weighted graph
Input:
• A weighted graph
• Starting vertex
• Destination vertex
Output:
A graph which connects all the vertices with least
distance

3. Dijkstra's Algorithm
Input:
a weighted digraph G=(V,E) with positive edge weights
a source node s V∈
Initialization:
d[s]=0
for each vertex x V-s∈
d[x]=infinity
Mark all the vertices as unprocessed
Iteration:
for i=1 to |V|
Choose an unprocessed vertex x from V with minimum d[x]
Mark x as processed
for all y adj(x)∈
if d[y] > d[x]+w(x,y)
d[y] = d[x]+w(x,y)

4. Dijkstra's Algorithm With PATH
Input:
a weighted digraph G=(V,E) with positive edge weights
a source node s V∈
Initialization:
d[s]=0 predecessor [ s ] = undefined
for each vertex x V-s∈
d[x]=infinity
Mark all the vertices as unprocessed
Iteration:
for i=1 to |V|
Choose an unprocessed vertex x from V with minimum d[x]
Mark x as processed
for all y adj(x)∈
if d[y] > d[x]+w(x,y)
d[y] = d[x]+w(x,y)
predecessor [ y ] = x

5. Printing the Distance and path
for each vertex v
{
print Distance d[v]
print_path(v);
}
print_path(v)
{
if (v is undefined)
return;
else
print_path ( prdecessor[v] ); // note recursion
print v
}

6. C Code
for(i=1; i<=numofvertices; i++)
{
printf("nDistance : %d ::: Path: ",distance[i]);
print_path(i);
}
void print_path(int i)
{
if (i==-1)
return;
else
print_path(prdecessor[i]);
Assumes that vertices are
numbered from 1.
distance array and
predecessor array are
computed by dijkstra
algorithm
-1 is undefined vertex

7. Dijkstra's Shortest Path Algorithm
Find shortest path from s to t.
7
s
3
t
2
6
7
4
5
24
18
2
9
14
15
5
30
20
44
16
11
6
19
6

8. Dijkstra's Shortest Path Algorithm 8
s
3
t
2
6
7
4
5
24
18
2
9
14
15
5
30
20
44
16
11
6
19
6
∞
∞
∞
∞
∞
∞
∞
0
distance label
S = { }
PQ = { s, 2, 3, 4, 5, 6, 7, t }

9. Dijkstra's Shortest Path Algorithm 9
s
3
t
2
6
7
4
5
24
18
2
9
14
15
5
30
20
44
16
11
6
19
6
∞
∞
∞
∞
∞
∞
∞
0
distance label
S = { }
PQ = { s, 2, 3, 4, 5, 6, 7, t }
delmin

10. Dijkstra's Shortest Path Algorithm
10
s
3
t
2
6
7
4
5
24
18
2
9
14
15
5
30
20
44
16
11
6
19
6
15
9
∞
∞
∞
14
∞
0
distance label
S = { s }
PQ = { 2, 3, 4, 5, 6, 7, t }
decrease key
∞X
∞
∞X
X

11. Dijkstra's Shortest Path Algorithm 11
s
3
t
2
6
7
4
5
24
18
2
9
14
15
5
30
20
44
16
11
6
19
6
15
9
∞
∞
∞
14
∞
0
distance label
S = { s }
PQ = { 2, 3, 4, 5, 6, 7, t }
∞X
∞
∞X
X
delmin

12. Dijkstra's Shortest Path Algorithm
12
s
3
t
2
6
7
4
5
24
18
2
9
14
15
5
30
20
44
16
11
6
19
6
15
9
∞
∞
∞
14
∞
0
S = { s, 2 }
PQ = { 3, 4, 5, 6, 7, t }
∞X
∞
∞X
X

13. Dijkstra's Shortest Path Algorithm
13
s
3
t
2
6
7
4
5
24
18
2
9
14
15
5
30
20
44
16
11
6
19
6
15
9
∞
∞
∞
14
∞
0
S = { s, 2 }
PQ = { 3, 4, 5, 6, 7, t }
∞X
∞
∞X
X
decrease key
X 33

14. Dijkstra's Shortest Path Algorithm
14
s
3
t
2
6
7
4
5
24
18
2
9
14
15
5
30
20
44
16
11
6
19
6
15
9
∞
∞
∞
14
∞
0
S = { s, 2 }
PQ = { 3, 4, 5, 6, 7, t }
∞X
∞
∞X
X
X 33
delmin

15. Dijkstra's Shortest Path Algorithm15
s
3
t
2
6
7
4
5
24
18
2
9
14
15
5
30
20
44
16
11
6
19
6
15
9
∞
∞
∞
14
∞
0
S = { s, 2, 6 }
PQ = { 3, 4, 5, 7, t }
∞X
∞
∞X
X
X 33
44
X
X
32

16. Dijkstra's Shortest Path Algorithm16
s
3
t
2
6
7
4
5
24
18
2
9
14
15
5
30
20
44
16
11
6
19
6
15
9
∞
∞
14
∞
0
S = { s, 2, 6 }
PQ = { 3, 4, 5, 7, t }
∞X
∞
∞X
X
44
X
delmin
∞X 33X
32

17. Dijkstra's Shortest Path Algorithm
17
s
3
t
2
6
7
4
5
18
2
9
14
15
5
30
20
44
16
11
6
19
6
15
9
∞
∞
14
∞
0
S = { s, 2, 6, 7 }
PQ = { 3, 4, 5, t }
∞X
∞
∞X
X
44
X
35X
59 X
24
∞X 33X
32

18. Dijkstra's Shortest Path Algorithm 18
s
3
t
2
6
7
4
5
24
18
2
9
14
15
5
30
20
44
16
11
6
19
6
15
9
∞
∞
14
∞
0
S = { s, 2, 6, 7 }
PQ = { 3, 4, 5, t }
∞X
∞
∞X
X
44
X
35X
59 X
delmin
∞X 33X
32

19. Dijkstra's Shortest Path Algorithm
19
s
3
t
2
6
7
4
5
24
18
2
9
14
15
5
30
20
44
16
11
6
19
6
15
9
∞
∞
14
∞
0
S = { s, 2, 3, 6, 7 }
PQ = { 4, 5, t }
∞X
∞
∞X
X
44
X
35X
59 XX51
X 34
∞X 33X
32

20. Dijkstra's Shortest Path Algorithm
20
s
3
t
2
6
7
4
5
18
2
9
14
15
5
30
20
44
16
11
6
19
6
15
9
∞
∞
14
∞
0
S = { s, 2, 3, 6, 7 }
PQ = { 4, 5, t }
∞X
∞
∞X
X
44
X
35X
59 XX51
X 34
delmin
∞X 33X
32
24

21. Dijkstra's Shortest Path Algorithm
21
s
3
t
2
6
7
4
5
18
2
9
14
15
5
30
20
44
16
11
6
19
6
15
9
∞
∞
14
∞
0
S = { s, 2, 3, 5, 6, 7 }
PQ = { 4, t }
∞X
∞
∞X
X
44
X
35X
59 XX51
X 34
24
X50
X45
∞X 33X
32

22. Dijkstra's Shortest Path Algorithm
22
s
3
t
2
6
7
4
5
18
2
9
14
15
5
30
20
44
16
11
6
19
6
15
9
∞
∞
14
∞
0
S = { s, 2, 3, 5, 6, 7 }
PQ = { 4, t }
∞X
∞
∞X
X
44
X
35X
59 XX51
X 34
24
X50
X45
delmin
∞X 33X
32

23. Dijkstra's Shortest Path Algorithm 23
s
3
t
2
6
7
4
5
18
2
9
14
15
5
30
20
44
16
11
6
19
6
15
9
∞
∞
14
∞
0
S = { s, 2, 3, 4, 5, 6, 7 }
PQ = { t }
∞X
∞
∞X
X
44
X
35X
59 XX51
X 34
24
X50
X45
∞X 33X
32

24. Dijkstra's Shortest Path Algorithm
24
s
3
t
2
6
7
4
5
18
2
9
14
15
5
30
20
44
16
11
6
19
6
15
9
∞
∞
14
∞
0
S = { s, 2, 3, 4, 5, 6, 7 }
PQ = { t }
∞X
∞
∞X
X
44
X
35X
59 XX51
X 34
X50
X45
delmin
∞X 33X
32
24

25. Dijkstra's Shortest Path Algorithm 25
s
3
t
2
6
7
4
5
24
18
2
9
14
15
5
30
20
44
16
11
6
19
6
15
9
∞
∞
14
∞
0
S = { s, 2, 3, 4, 5, 6, 7, t }
PQ = { }
∞X
∞
∞X
X
44
X
35X
59 XX51
X 34
X50
X45
∞X 33X
32

26. Dijkstra's Shortest Path Algorithm 26
s
3
t
2
6
7
4
5
24
18
2
9
14
15
5
30
20
44
16
11
6
19
6
15
9
∞
∞
14
∞
0
S = { s, 2, 3, 4, 5, 6, 7, t }
PQ = { }
∞X
∞
∞X
X
44
X
35X
59 XX51
X 34
X50
X45
∞X 33X
32

28. ASSESSMENT

29. Single Source Shortest Path
1
2
76
5
4
3
5
3
1
7
5
4
9
4
6
8
1
4
1