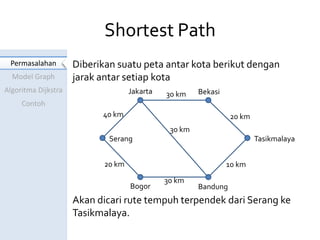
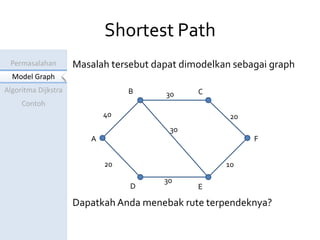
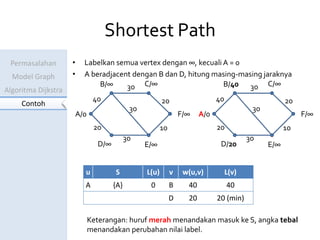
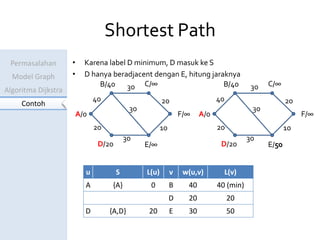
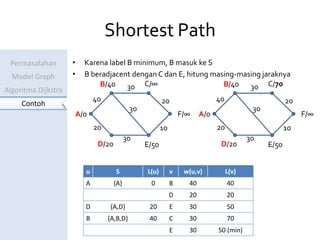
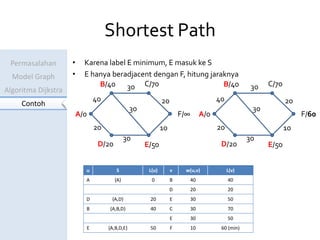
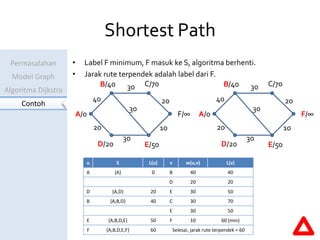
Dokumen ini menjelaskan algoritma Dijkstra untuk menentukan jarak terpendek antara kota-kota yang dihubungkan dalam model graf. Contoh perhitungan jarak dari Serang ke Tasikmalaya menunjukkan langkah-langkah algoritma dan pembaruan label pada setiap iterasi. Hasil akhirnya adalah jarak terpendek yang ditemukan adalah 60 km.

1. Algoritma Dijkstra
Menentukan Jarak Terpendek
Onggo Wr
@OnggoWr

2. Shortest Path
Permasalahan Diberikan suatu peta antar kota berikut dengan
Model Graph jarak antar setiap kota
Algoritma Dijkstra Jakarta Bekasi
30 km
Contoh
40 km 20 km
30 km
Serang Tasikmalaya
20 km 10 km
30 km
Bogor Bandung
Akan dicari rute tempuh terpendek dari Serang ke
Tasikmalaya.

3. Shortest Path
Permasalahan Masalah tersebut dapat dimodelkan sebagai graph
Model Graph
Algoritma Dijkstra B C
30
Contoh
40 20
30
A F
20 10
30
D E
Dapatkah Anda menebak rute terpendeknya?

4. Shortest Path
Permasalahan Masalah ini dapat diselesaikan dengan algoritma Dijkstra:
Model Graph
procedure Dijkstra
Algoritma Dijkstra {G has vertices a = V0, V1, . . . , Vn = z and weights w(Vi, Vj) where w(Vi, Vj) = ∞ if
{Vi, Vj} is not an edge in G}
Contoh for i : = 1 to n
L(Vi):=∞
L(a) := 0
S := 
{the labels are now initialized so that the label of a is 0 and all other labels are
∞, and S is the empty set }
while z  S
begin
u := a vertex not in S with L(u) minimal
S := S  {u}
for all vertices v not in S
if L(u) + w(u, v) < L(v) then L(v) := L(u) + w(u, v)
{this adds a vertex to S with minimal label and updates the labels of
vertices not in S}
end
{L(z) = length of a shortest path from a to z}

5. Shortest Path
Permasalahan • Labelkan semua vertex dengan ∞, kecuali A = 0
Model Graph • A beradjacent dengan B dan D, hitung masing-masing jaraknya
Algoritma Dijkstra
B/∞ 30 C/∞ B/40 30 C/∞
40 20 40 20
Contoh
30 30
A/0 F/∞ A/0 F/∞
20 10 20 10
30 30
D/∞ E/∞ D/20 E/∞
u S L(u) v w(u,v) L(v)
A {A} 0 B 40 40
D 20 20 (min)
Keterangan: huruf merah menandakan masuk ke S, angka tebal
menandakan perubahan nilai label.

6. Shortest Path
Permasalahan • Karena label D minimum, D masuk ke S
Model Graph • D hanya beradjacent dengan E, hitung jaraknya
B/40 30 C/∞ B/40 30 C/∞
Algoritma Dijkstra
40 20 40 20
Contoh
30 30
A/0 F/∞ A/0 F/∞
20 10 20 10
30 30
D/20 E/∞ D/20 E/50
u S L(u) v w(u,v) L(v)
A {A} 0 B 40 40 (min)
D 20 20
D {A,D} 20 E 30 50

7. Shortest Path
Permasalahan • Karena label B minimum, B masuk ke S
Model Graph • B beradjacent dengan C dan E, hitung masing-masing jaraknya
B/40 30 C/∞ B/40 30 C/70
Algoritma Dijkstra
40 20 40 20
Contoh
30 30
A/0 F/∞ A/0 F/∞
20 10 20 10
30 30
D/20 E/50 D/20 E/50
u S L(u) v w(u,v) L(v)
A {A} 0 B 40 40
D 20 20
D {A,D} 20 E 30 50
B {A,B,D} 40 C 30 70
E 30 50 (min)

8. Shortest Path
Permasalahan • Karena label E minimum, E masuk ke S
Model Graph • E hanya beradjacent dengan F, hitung jaraknya
B/40 30 C/70 B/40 30 C/70
Algoritma Dijkstra
40 20 40 20
Contoh
30 30
A/0 F/∞ A/0 F/60
20 10 20 10
30 30
D/20 E/50 D/20 E/50
u S L(u) v w(u,v) L(v)
A {A} 0 B 40 40
D 20 20
D {A,D} 20 E 30 50
B {A,B,D} 40 C 30 70
E 30 50
E {A,B,D,E} 50 F 10 60 (min)

9. Shortest Path
Permasalahan • Label F minimum, F masuk ke S, algoritma berhenti.
Model Graph • Jarak rute terpendek adalah label dari F.
B/40 30 C/70 B/40 30 C/70
Algoritma Dijkstra
40 20 40 20
Contoh
30 30
A/0 F/∞ A/0 F/∞
20 10 20 10
30 30
D/20 E/50 D/20 E/50
u S L(u) v w(u,v) L(v)
A {A} 0 B 40 40
D 20 20
D {A,D} 20 E 30 50
B {A,B,D} 40 C 30 70
E 30 50
E {A,B,D,E} 50 F 10 60 (min)
F {A,B,D,E,F} 60 Selesai, jarak rute terpendek = 60

10. Tugas
Permasalahan • Tentukan jarak dan rute terpendek dari a ke z dengan
menggunakan Algoritma Dijkstra untuk jaringan berikut ini.
Model Graph
Algoritma Dijkstra
Contoh