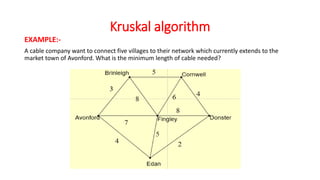
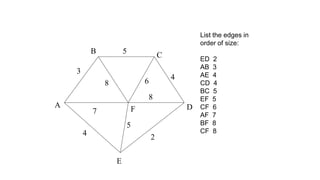
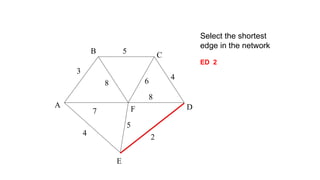
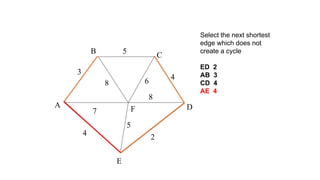
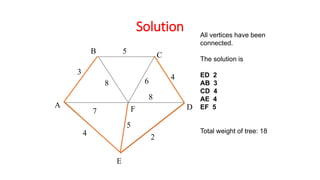
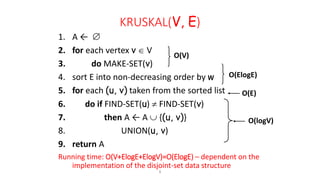
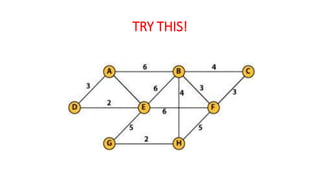
Kruskal's algorithm is a minimum spanning tree algorithm that finds the minimum cost collection of edges that connect all vertices in a connected, undirected graph. It works by sorting the edges by weight and then sequentially adding the shortest edge that does not create a cycle. The algorithm uses a disjoint set data structure to track connected components in the graph. It runs in O(ElogE) time, where E is the number of edges.

1. KRUSKAL’S ALGORITHM
MADE BY :-
DHRUV PATEL(160110116029).
BHAVIK VASHI(160110116061).

2. Introduction
• Kruskal's algorithm is a minimum-spanning-tree algorithm which finds an edge of the least
possible weight that connects any two trees in the forest.
• Some key terms:-
1. spanning tree:- A spanning tree of a connected, undirected graph G is a sub-graph of G which is
a tree that connects all the vertices together.
2. forest:- A forest is a disjoint union of trees, or equivalently an acyclic graph that is not
necessarily connected.

3. Kruskal algorithm
EXAMPLE:-
A cable company want to connect five villages to their network which currently extends to the
market town of Avonford. What is the minimum length of cable needed?

4. A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
List the edges in
order of size:
ED 2
AB 3
AE 4
CD 4
BC 5
EF 5
CF 6
AF 7
BF 8
CF 8

5. Select the shortest
edge in the network
ED 2
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8

6. Select the next shortest
edge which does not
create a cycle
ED 2
AB 3
CD 4
AE 4
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8

7. All vertices have been
connected.
The solution is
ED 2
AB 3
CD 4
AE 4
EF 5
Total weight of tree: 18
A
F
B
C
D
E
2
7
4
5
8 6
4
5
3
8
Solution

8. 8
1. A ← 
2. for each vertex v  V
3. do MAKE-SET(v)
4. sort E into non-decreasing order by w
5. for each (u, v) taken from the sorted list
6. do if FIND-SET(u)  FIND-SET(v)
7. then A ← A  {(u, v)}
8. UNION(u, v)
9. return A
Running time: O(V+ElogE+ElogV)=O(ElogE) – dependent on the
implementation of the disjoint-set data structure
KRUSKAL(V, E)
O(V)
O(ElogE)
O(E)
O(logV)

9. Disjoint data structure
• MAKE-SET(u) – creates a new set whose only member is u
• FIND-SET(u) – returns a representative element from the set that contains u
• UNION(u, v) – unites the dynamic sets that contain u and v, say Su and Sv
• E.g.: Su = {r, s, t, u}, Sv = {v, x, y}
UNION (u, v) = {r, s, t, u, v, x, y}
• Running time for FIND-SET and UNION depends on implementation.
• Can be shown to be α(n)=O(logn) where α() is a very slowly growing function.

10. TRY THIS!