The document discusses the multivariate normal distribution. Some key points:
- The multivariate normal distribution generalizes the univariate normal distribution to multiple dimensions. It plays an important role in multivariate analysis.
- The multivariate normal density depends on a mean vector μ and covariance matrix Σ. It takes the form of an exponential function involving the difference between the data vector x and the mean μ, multiplied by the inverse of the covariance matrix Σ.
- Properties of the multivariate normal include: linear combinations of components are normally distributed; subsets are normally distributed; zero covariance implies independence of components; conditional distributions are normal.


![3.2 The Multivariate Normal density and Its Properties
• Recall that the univariate normal distribution, with mean µ and variance σ2
,
has the probability density function
f(x) =
1
√
2πσ2
e−[(x−µ)/σ]2
/2
− ∞ < x < ∞
• The term
x − µ
σ
2
= (x − µ)(σ2
)−1
(x − µ)
• This can be generalized for p × 1 vector x of observations on serval variables
as
(x − µ)0
Σ−1
(x − µ)
The p × 1 vector µ represents the expected value of the random vector X,
and the p × p matrix Σ is the variance-covariance matrix of X.
3](https://image.slidesharecdn.com/multivariatenormaldistribution-230727194445-1900bde5/85/multivariate-normal-distribution-pdf-3-320.jpg)
![• A p-dimensional normal density for the random vector X0
= [X1, X2, . . . , Xp]
has the form
f(x) =
1
(2π)p/2|Σ|1/2
e−(x−µ)0
Σ−1
(x−µ)/2
where −∞ xi ∞, i = 1, 2, . . . , p. We should denote this p-dimensional
normal density by Np(µ, Σ).
4](https://image.slidesharecdn.com/multivariatenormaldistribution-230727194445-1900bde5/85/multivariate-normal-distribution-pdf-4-320.jpg)






![Result 3.2 If X is distributed as Np(µ, Σ), then any linear combination of
variables a0
X = a1X1 +a2X2 +· · ·+apXp is distributed as N(a0
µ, a0
Σa). Also
if a0
X is distributed as N(a0
µ, a0
Σa) for every a, then X must be Np(µ, Σ).
Example 3.3 (The distribution of a linear combination of the component
of a normal random vector) Consider the linear combination a0
X of a
multivariate normal random vector determined by the choice a0
= [1, 0, . . . , 0].
Result 3.3 If X is distributed as Np(µ, Σ), the q linear combinations
A(q×p)Xp×1 =
a11X1 + · · · + a1pXp
a21X1 + · · · + a2pXp
.
.
.
aq1X1 + · · · + aqpXp
are distributed as Nq(Aµ, AΣA0
). Also Xp×1 + dp×1, where d is a vector of
constants, is distributed as Np(µ + d, Σ).
11](https://image.slidesharecdn.com/multivariatenormaldistribution-230727194445-1900bde5/85/multivariate-normal-distribution-pdf-11-320.jpg)

![Result 3.4 All subsets of X are normally distributed. If we respectively partition
X, its mean vector µ, and its covariance matrix Σ as
X(p×1) =
X1
(q × 1)
· · · · · ·
X2
(p − q) × 1
µ(p×1) =
µ1
(q × 1)
· · · · · ·
µ2
(p − q) × 1
and
Σ(p×p) =
Σ11 Σ12
(q × 1) (q × (p − q))
· · · · · · · · · · · ·
Σ21 Σ22
((p − q) × q) ((p − q) × (p − q))
then X1 is distributed as Nq(µ1, Σ11).
Example 3.5 (The distribution of a subset of a normal random vector)
If X is distributed as N5(µ, Σ), find the distribution of [X2, X4]0
.
13](https://image.slidesharecdn.com/multivariatenormaldistribution-230727194445-1900bde5/85/multivariate-normal-distribution-pdf-13-320.jpg)




![Example 3.8 (Linear combinations of random vectors) Let X1, X2, X3
and X4 be independent and identically distributed 3 × 1 random vectors with
µ =
3
−1
1
and Σ =
3 −1 1
−1 1 0
1 0 2
(a) find the mean and variance of the linear combination a0
X1 of the three
components of X1 where a = [a1 a2 a3]0
.
(b) Consider two linear combinations of random vectors
1
2
X1 +
1
2
X2 +
1
2
X3 +
1
2
X4
and
X1 + X2 + X3 − 3X4.
Find the mean vector and covariance matrix for each linear combination of
vectors and also the covariance between them.
18](https://image.slidesharecdn.com/multivariatenormaldistribution-230727194445-1900bde5/85/multivariate-normal-distribution-pdf-18-320.jpg)








![4.5 Large-Sample Behavior of X̄ and S
Result 3.12 (Law of Large numbers) Let Y1, Y2, . . . , Yn be independent
observations from a population with mean E(Yi) = µ, then
Ȳ =
Y1 + Y2 + · · · + Yn
n
converges in probability to µ as n increases without bound. That is, for any
prescribed accuracy ε 0, P[−ε Ȳ − µ ε] approaches unity as n → ∞.
Result 3.13 (The central limit theorem) Let X1, X2, . . . , Xn be independent
observations from any population with mean µ and finite covariance Σ. Then
√
n(X̄ − µ) has an approximate Np(0, Σ)distribution
for large sample sizes. Here n should also be large relative to p.
27](https://image.slidesharecdn.com/multivariatenormaldistribution-230727194445-1900bde5/85/multivariate-normal-distribution-pdf-27-320.jpg)





![• Plots are always useful devices in any data analysis. Special plots called
Q − Q plots can be used to assess the assumption of normality.
Let x(1) ≤ x(2) ≤ · · · ≤ x(n) represent these observations after they are
ordered according to magnitude. For a standard normal distribution, the
quantiles q(j) are defined by the relation
P[Z ≤ q(j)] =
Z q(j)
−∞
1
√
2π
e−z2
/2
dz = p(j) =
j − 1
2
n
Here p(j) is the probability of getting a value less than or equal to q(j) in a
single drawing from a standard normal population.
• The idea is to look at the pairs of quantiles (q(j), x(j)) with the same
associated cumulative probability (j − 1
2)/n. If the data arise from a normal
population, the pairs (q(j), x(j)) will be approximately linear related, since
σq(j) + µ is nearly expected sample quantile.
33](https://image.slidesharecdn.com/multivariatenormaldistribution-230727194445-1900bde5/85/multivariate-normal-distribution-pdf-33-320.jpg)




![Linear combinations of more than one characteristic can be investigated.
Many statistician suggest plotting
ê0
1xj where S ˆ
e1 = λ̂1 ˆ
e1
in which λ̂1 is the largest eigenvalue of S. Here x0
j = [xj1, xj2, . . . , xjp] is
the jth observation on p variables X1, X2, . . . , Xp. The linear combination
êpxj corresponding to the smallest eigenvalue is also frequently singled out for
inspection
38](https://image.slidesharecdn.com/multivariatenormaldistribution-230727194445-1900bde5/85/multivariate-normal-distribution-pdf-38-320.jpg)

















![• The procedure just described is equivalent to making each marginal
distribution approximately normal. Although normal marginals are not
sufficient to ensure that the joint distribution is normal, in practical
applications this may be good enough.
• If not, the value λ̂1, λ̂2, . . . , λ̂p can be obtained from the preceding
transformations and iterate toward the set of values λ0
= [λ1, λ2, . . . , λp],
which collectively maximizes
`(λ1, λ2, . . . , λp) = −
n
2
ln |S(λ)| + (λ1 − 1)
n
X
j=1
ln xj1 + (λ2 − 1)
n
X
j=1
ln xj2
+ · · · + (λp − 1)
n
X
j=1
ln xjp
where S(λ) is the sample covariance matrix computed from
x
(λ)
j =
xλ1
j1 − 1
λ1
,
xλ2
j2 − 1
λ2
, · · · ,
x
λp
jp − 1
λp
#0
, j = 1, 2, . . . , n
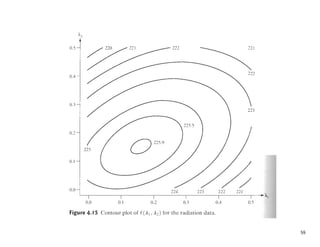
56](https://image.slidesharecdn.com/multivariatenormaldistribution-230727194445-1900bde5/85/multivariate-normal-distribution-pdf-56-320.jpg)