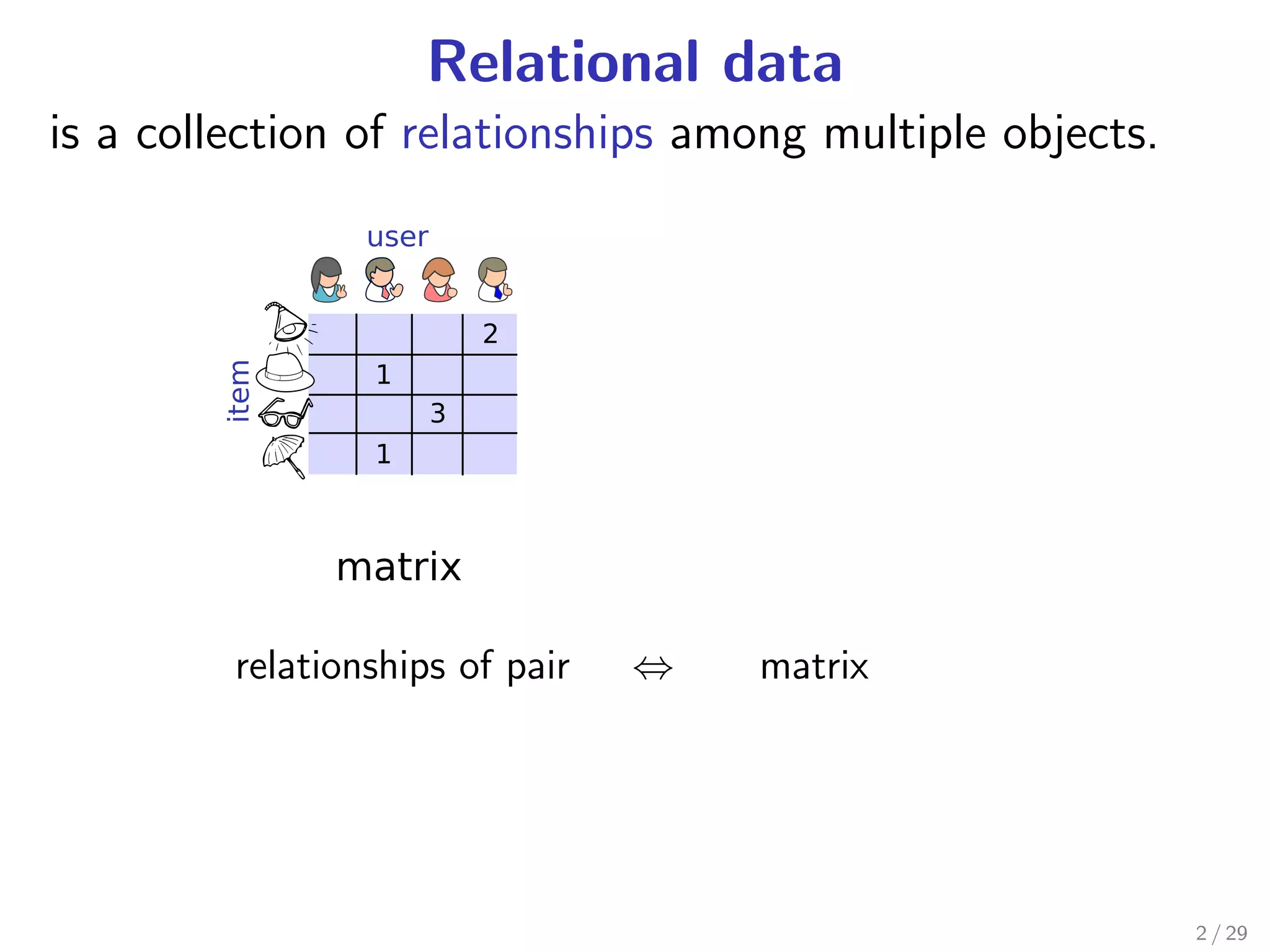
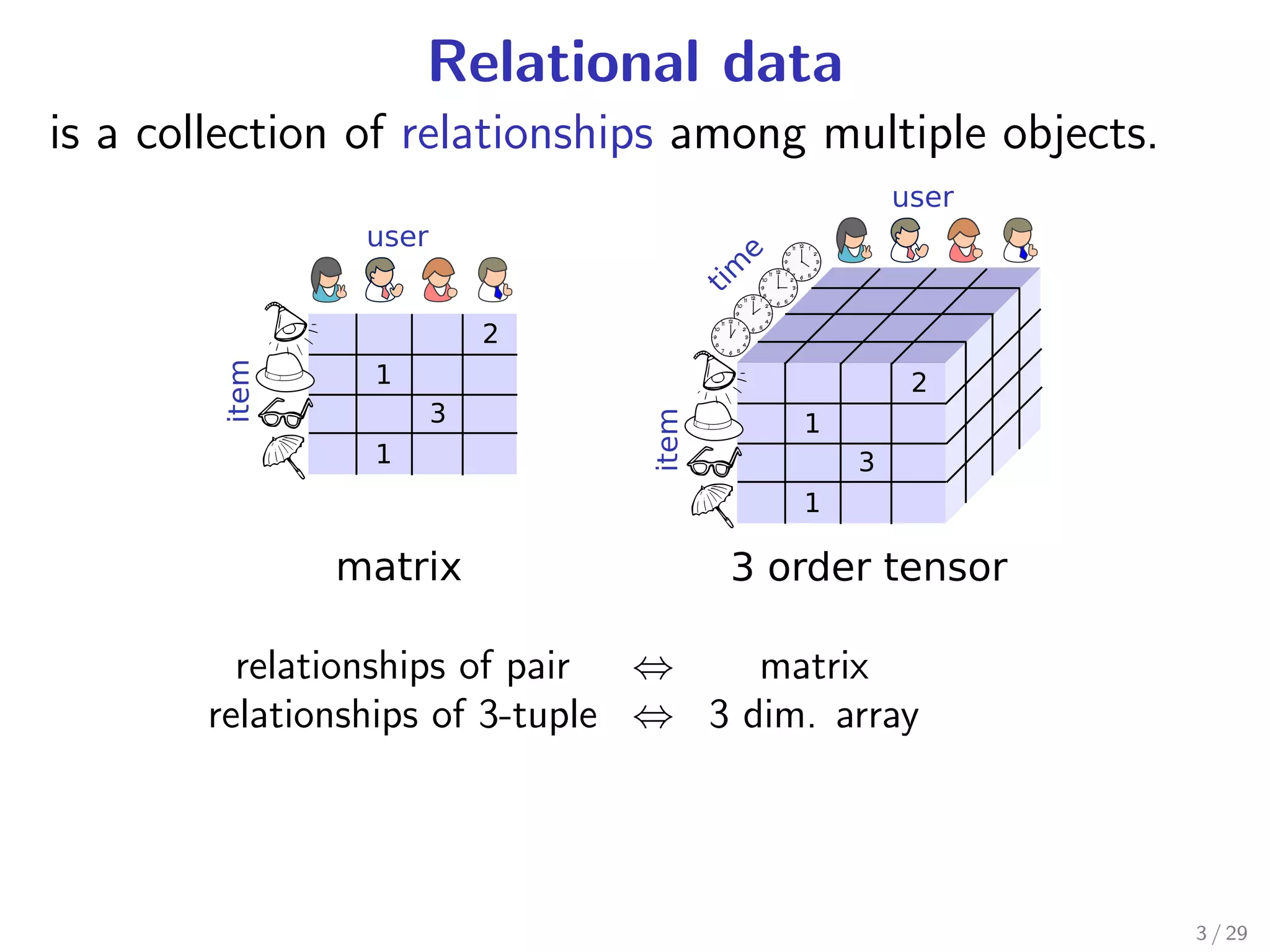
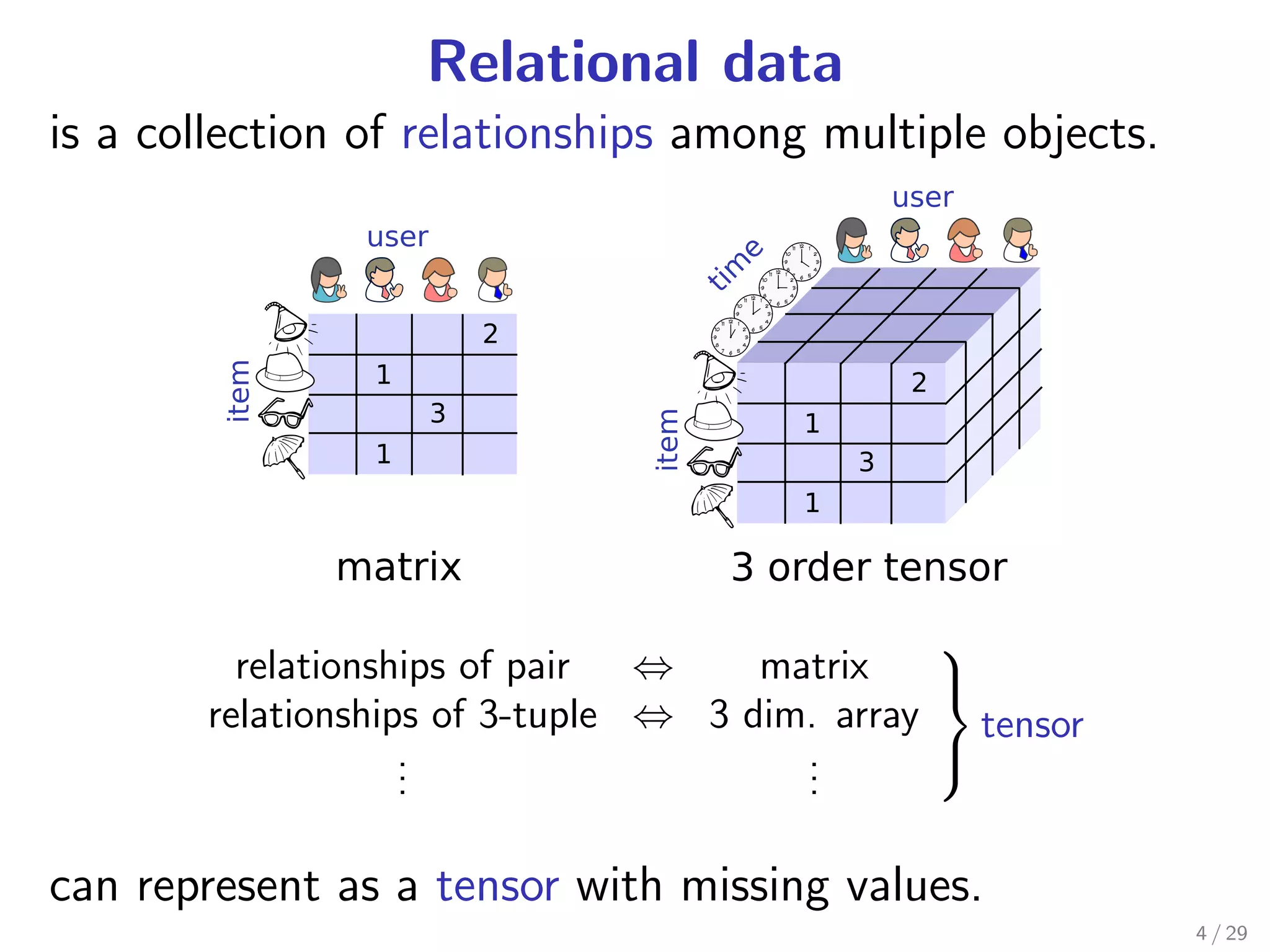
This document presents two tensor factorization methods: Exponential Family Tensor Factorization (ETF) and Full-Rank Tensor Completion (FTC). ETF generalizes Tucker decomposition by allowing for different noise distributions in the tensor and handles mixed discrete and continuous values. FTC completes missing tensor values without reducing dimensionality by kernelizing Tucker decomposition. The document outlines these methods and their motivations, discusses Tucker decomposition, and provides an example applying ETF to anomaly detection in time series sensor data.

1. Generalization of Tensor Factorization
and Applications
Kohei Hayashi
Collaborators:
T. Takenouchi, T. Shibata, Y. Kamiya, D. Kato, K. Kunieda, K. Yamada, K. Ikeda,
R. Tomioka, H. Kashima
May 14, 2012
1 / 29

2. Relational data
is a collection of relationships among multiple objects.
relationships of pair ⇔ matrix
2 / 29

3. Relational data
is a collection of relationships among multiple objects.
relationships of pair ⇔ matrix
relationships of 3-tuple ⇔ 3 dim. array
3 / 29

4. Relational data
is a collection of relationships among multiple objects.

relationships of pair ⇔ matrix 
relationships of 3-tuple ⇔ 3 dim. array tensor
.
. .
. 
. .
can represent as a tensor with missing values.
4 / 29

5. Issue of tensor representation
Tensor representation is generally high-dimensional and
large-scale
• e.g. 1, 000 users × 1, 000 items × 1, 000 times
= total 1, 000, 000, 000 relationships
Dimensional reduction techniques such as tensor
factorization is used.
5 / 29

6. Tensor factorization
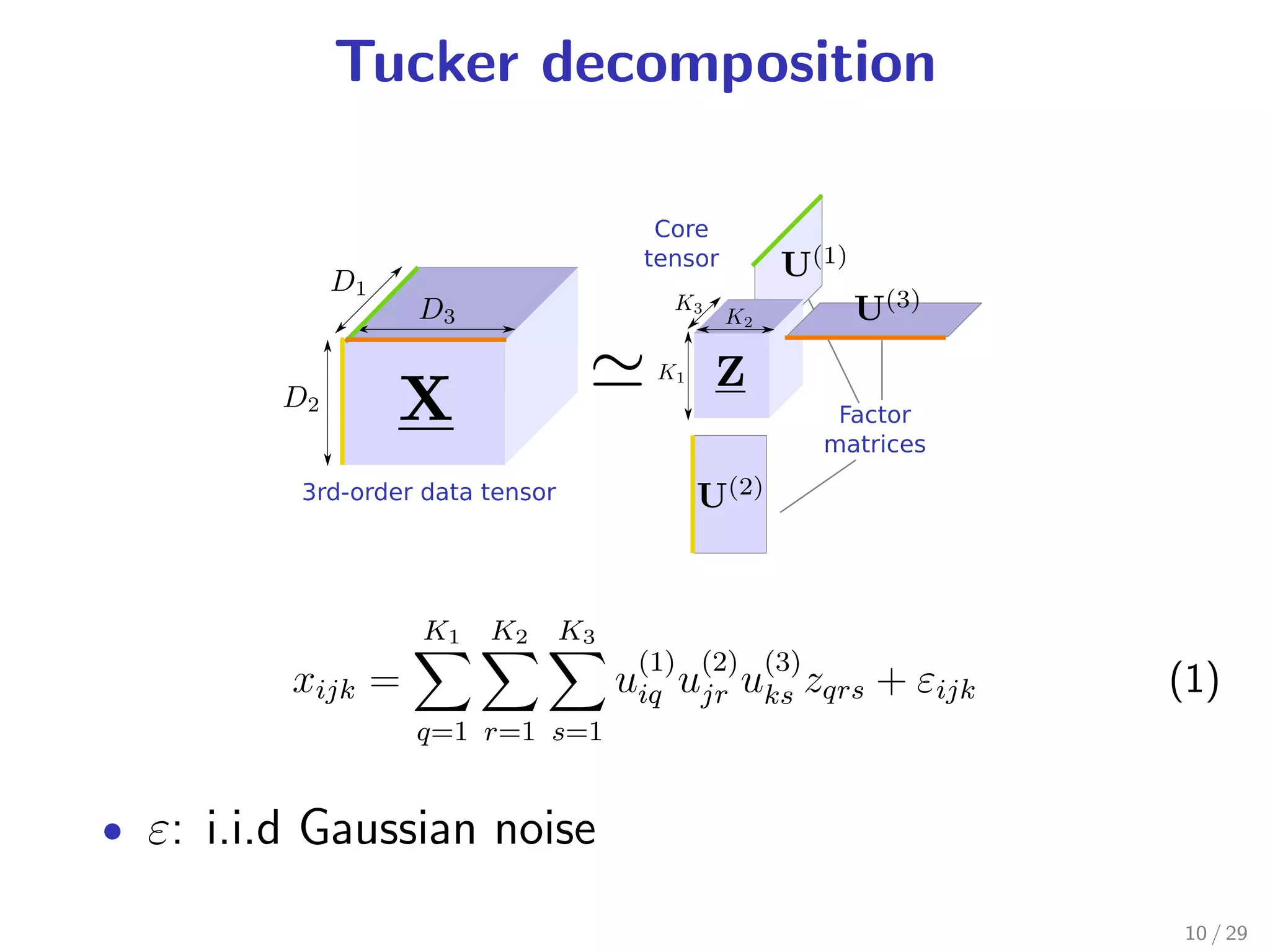
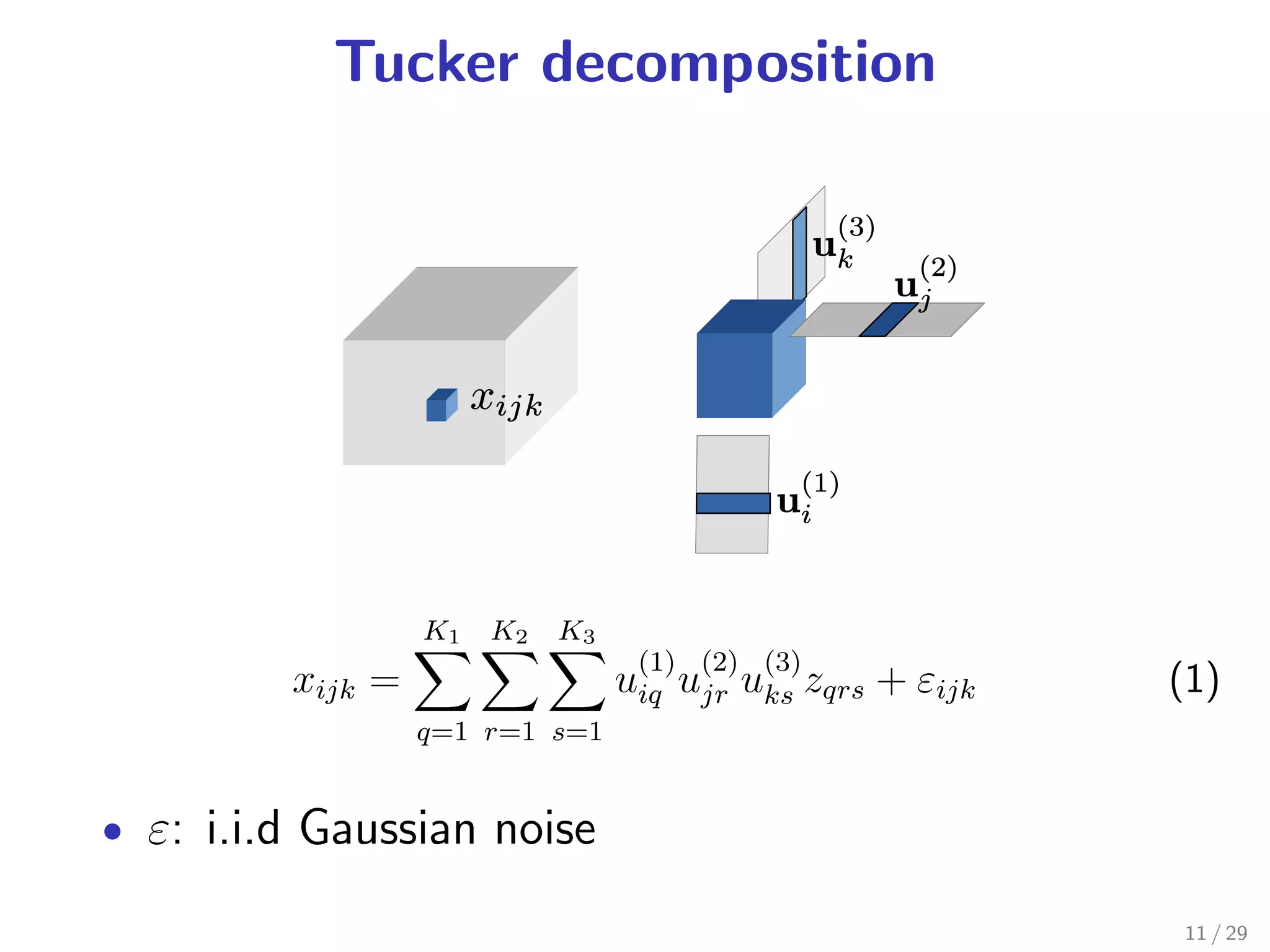
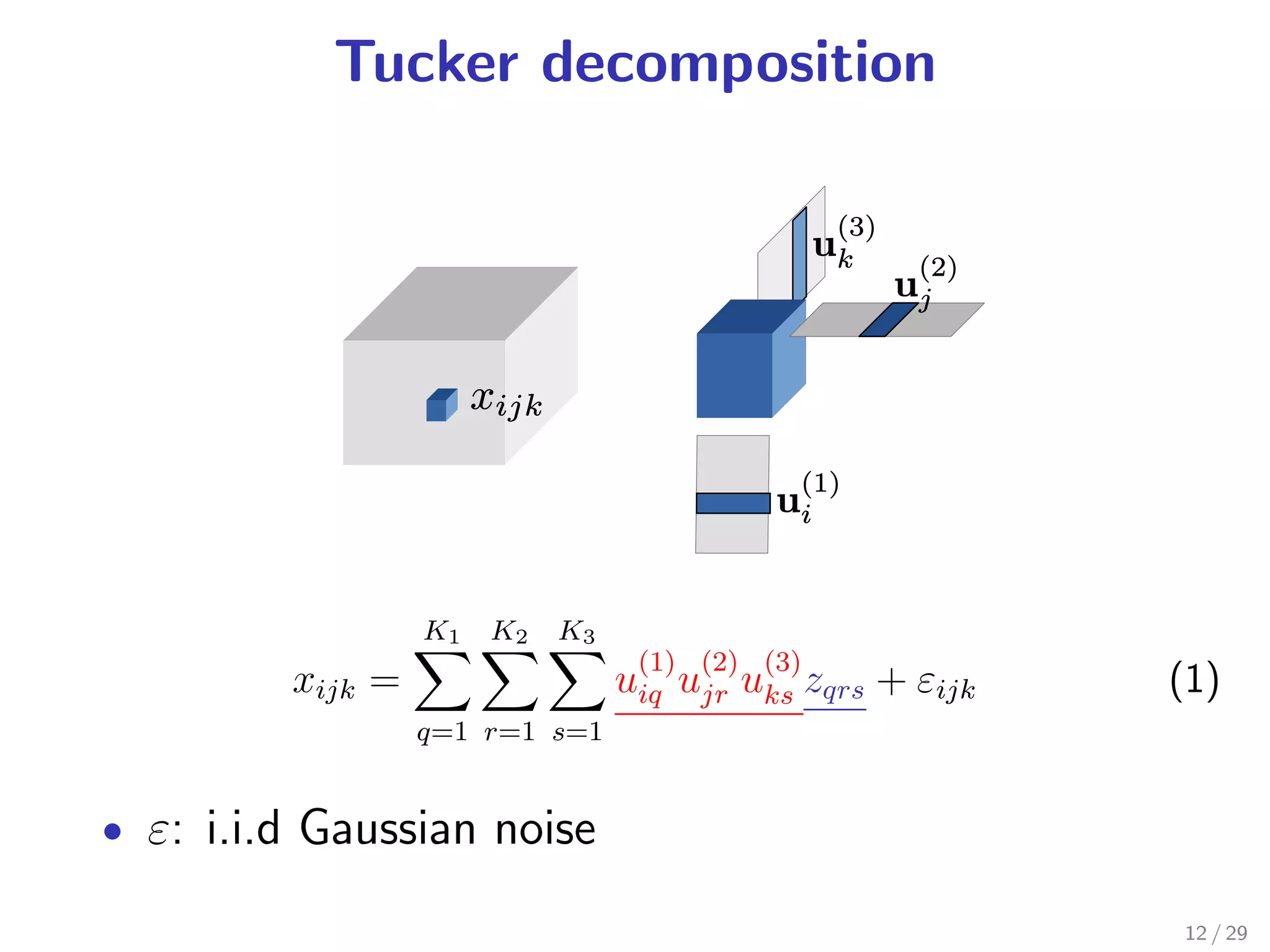
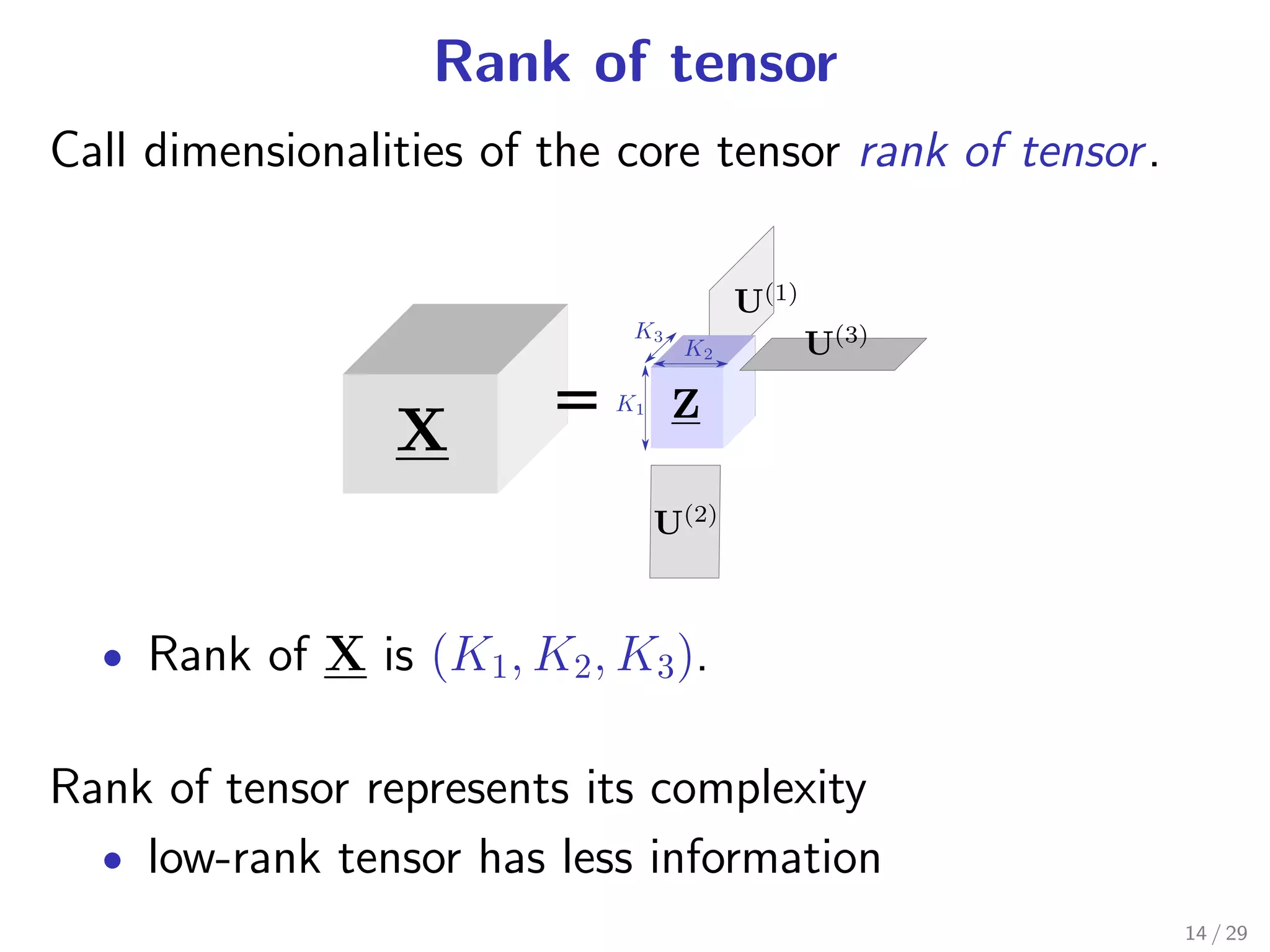
Tucker decomposition [Tucker 1966]: a tensor factorization
method assuming
1 observation noise is Gaussian
.
2 underlying tensor is low-dimensional
.
These assumptions are general ... but are not always
true.
6 / 29

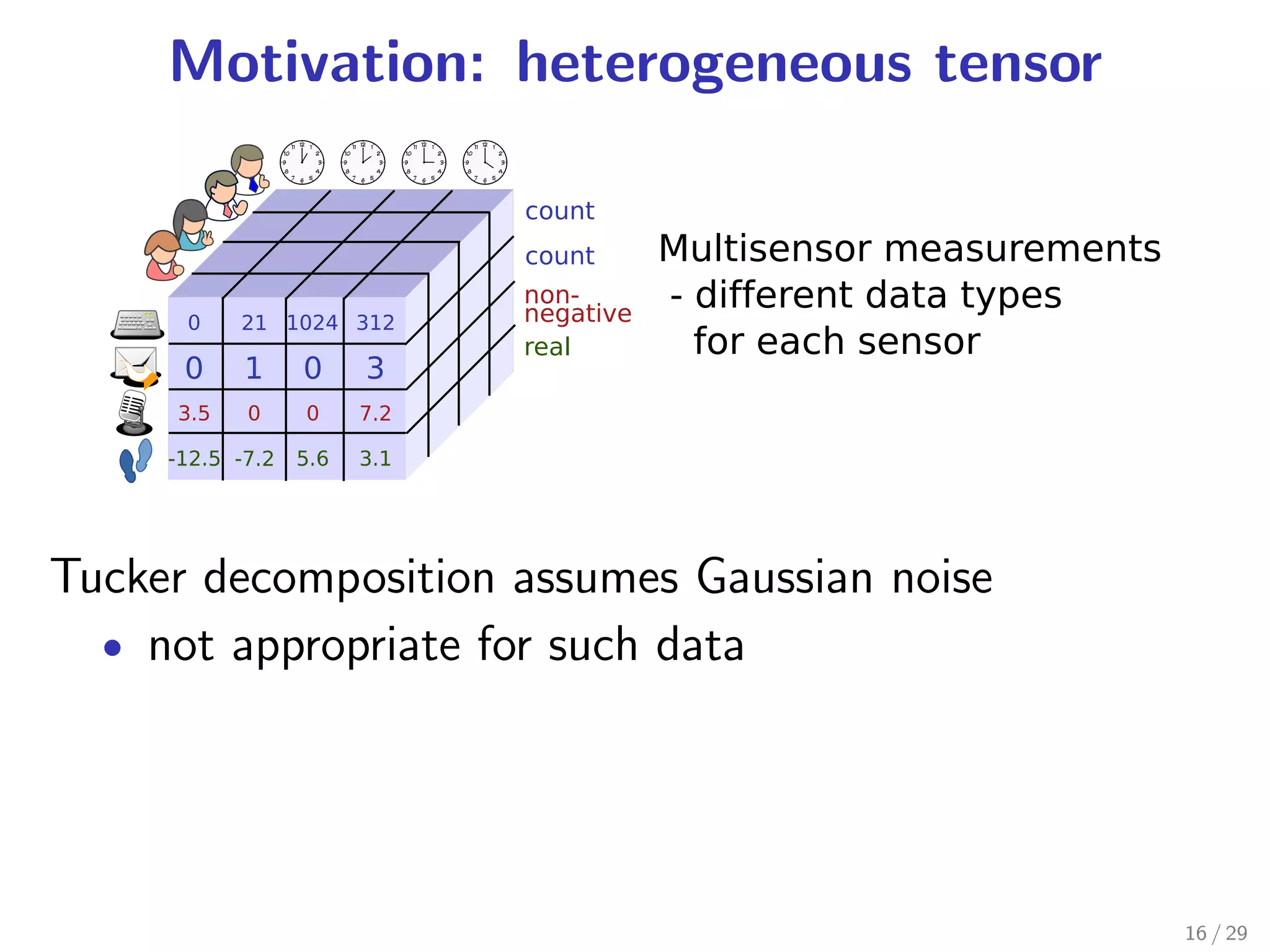
7. Contributions
Generalize Tucker decomposition and propose two new
models:
1 Exponential family tensor factorization (ETF)
.
[Joint work with Takenouchi, Shibata, Kamiya, Kunieda, Yamada, and
Ikeda]
• Generalize the noise distribution.
• Can handle a tensor containing mixed discrete and
continuous values.
2. Full-rank tensor completion (FTC)
[Joint work with Tomioka and Kashima]
• Kernelize Tucker decomposition
• Complete missing values without reducing the
dimensionality.
7 / 29

8. Outline
1. Tucker decomposition
2. Exponential family tensor factorization (ETF)
3. Full-rank tensor completion (FTC)
4. Conclusion
8 / 29

9. Outline
1. Tucker decomposition
2. Exponential family tensor factorization (ETF)
3. Full-rank tensor completion (FTC)
4. Conclusion
9 / 29

10. Tucker decomposition
K1 K2 K3
(1) (2) (3)
xijk = uiq ujr uks zqrs + εijk (1)
q=1 r=1 s=1
• ε: i.i.d Gaussian noise
10 / 29

11. Tucker decomposition
K1 K2 K3
(1) (2) (3)
xijk = uiq ujr uks zqrs + εijk (1)
q=1 r=1 s=1
• ε: i.i.d Gaussian noise
11 / 29

12. Tucker decomposition
K1 K2 K3
(1) (2) (3)
xijk = uiq ujr uks zqrs + εijk (1)
q=1 r=1 s=1
• ε: i.i.d Gaussian noise
12 / 29

13. Vectorized form
Let x ∈ RD and z ∈ RK denote vectorized X and Z,
resp., then
x = Wz + ε where W ≡ U(3) ⊗ U(2) ⊗ U(1) .
• D ≡ D1 D2 D3 , K ≡ K1 K2 K3
• ⊗: the Kronecker product
Tucker decomposition = A linear Gaussian model
x ∼ N (x | Wz, σ 2 I)
13 / 29

14. Rank of tensor
Call dimensionalities of the core tensor rank of tensor .
• Rank of X is (K1 , K2 , K3 ).
Rank of tensor represents its complexity
• low-rank tensor has less information
14 / 29

15. Outline
1. Tucker decomposition
2. Exponential family tensor factorization (ETF)
3. Full-rank tensor completion (FTC)
4. Conclusion
15 / 29

16. Motivation: heterogeneous tensor
Tucker decomposition assumes Gaussian noise
• not appropriate for such data
16 / 29

17. Motivation: heterogeneous tensor
Tucker decomposition assumes Gaussian noise
• not appropriate for such data
.
Approach
.
generalize Tucker decomposition, assuming a different
distribution for each element
.
17 / 29

18. Exponential family tensor factorization
.
Likelihood
.
D
x∼ Expond (xd | θd ), θ ≡ Wz
d=1 exp. family Tucker decomp.
. where Expon(x | θ) ≡ exp [xθ − ψ(θ) + F (x)]
exponential family : a class of distributions
Gaussian Poisson Bernoulli
0.4
0.7
Density
Density
0.2
0.2
0.5
(θ = 0)
0.0
0.0
0.3
ψ(θ) θ2−4 −2
/2 0 2 4
exp[θ] 4
0 2 6 8
ln(10.0 0.5 1.0 1.5
−0.5
+ exp[θ])
x
18 / 29

19. .
Priors
.
• for z: a Gaussian prior N (0, I)
(m) −1
. • for U : a Gaussian prior N (0, αm I)
.
Joint log-likelihood
.
D
L =x Wz − ψhd (wd z)
d=1
M
1 αm 2
− ||z||2 − U(m) + const.
2 m=1
2 Fro
.
Estimate parameters by Bayesian inference.
19 / 29

20. Bayesian inference
Marginal-MAP estimator:
argmax exp[L(z, U(1) , . . . , U(M ) )]dz
U(1) ,...,U(M )
• The integral is not analytical.
Develop efficient yet accurate approximation with
Laplace approximation and Gaussian process.
• Computational cost is still higher than Tucker
dcomp.
• For a long and thin tensor (e.g. time series), online
algorithm is applicable (see thesis.)
20 / 29

21. Experiments
21 / 29

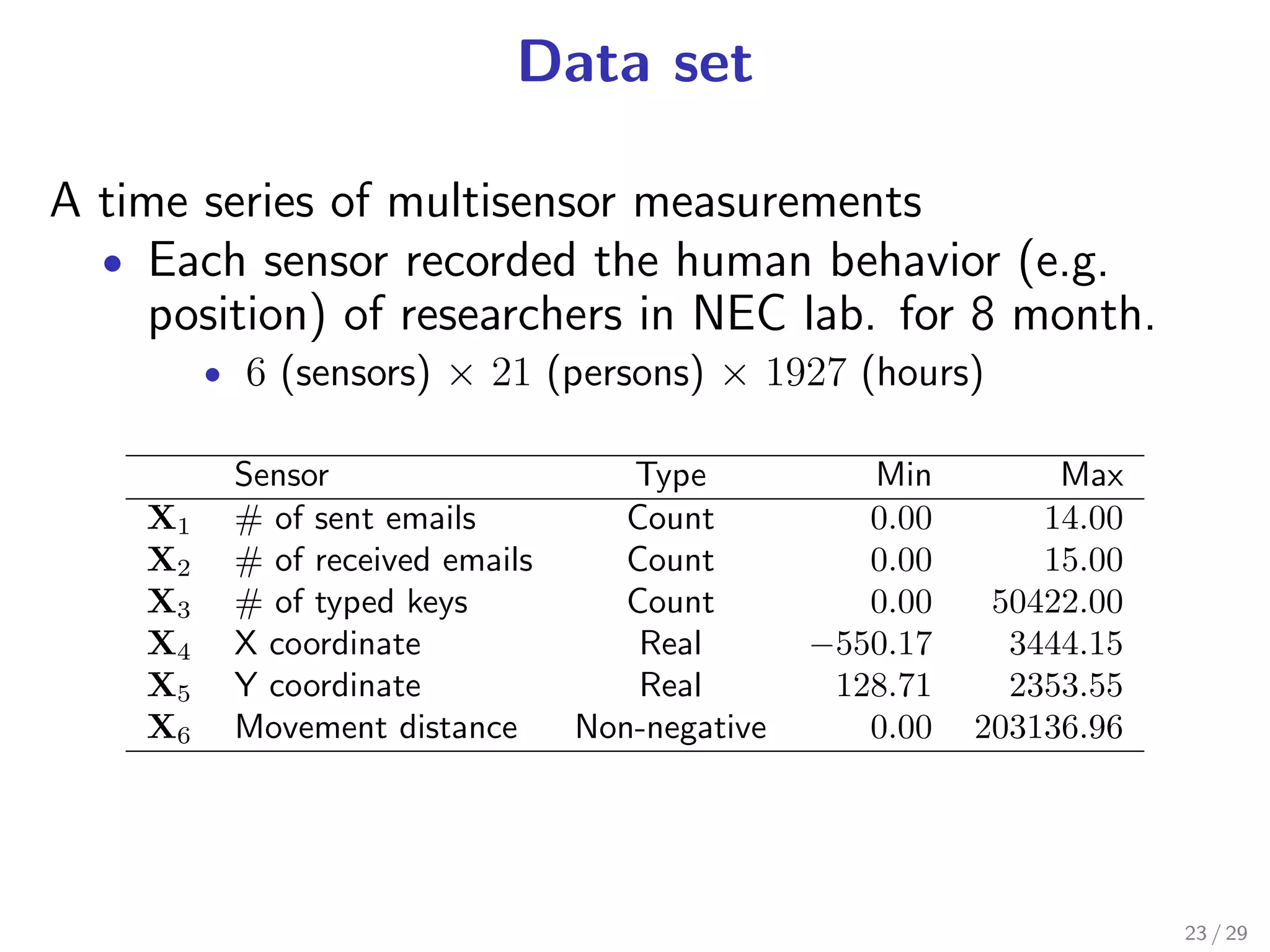
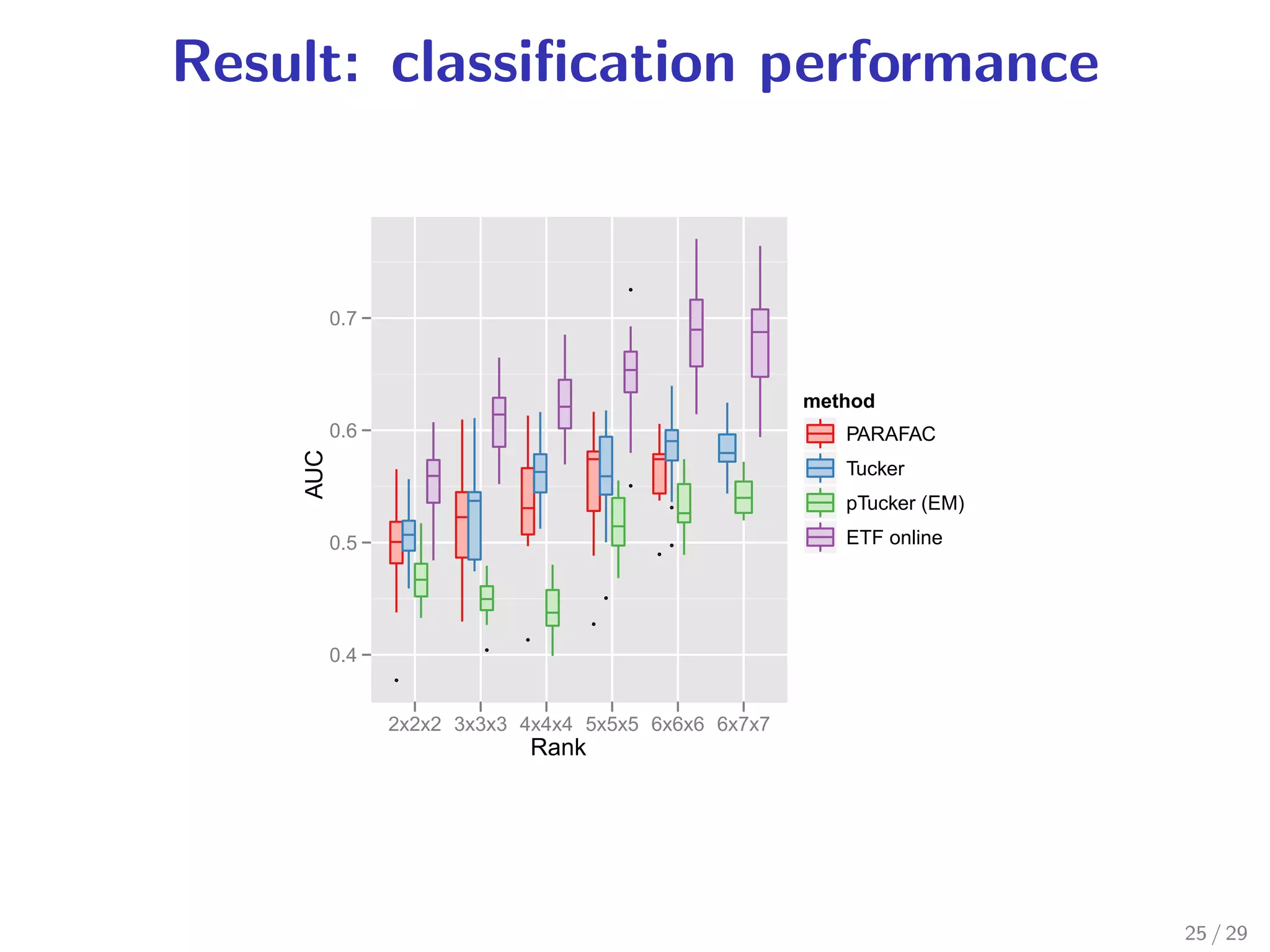
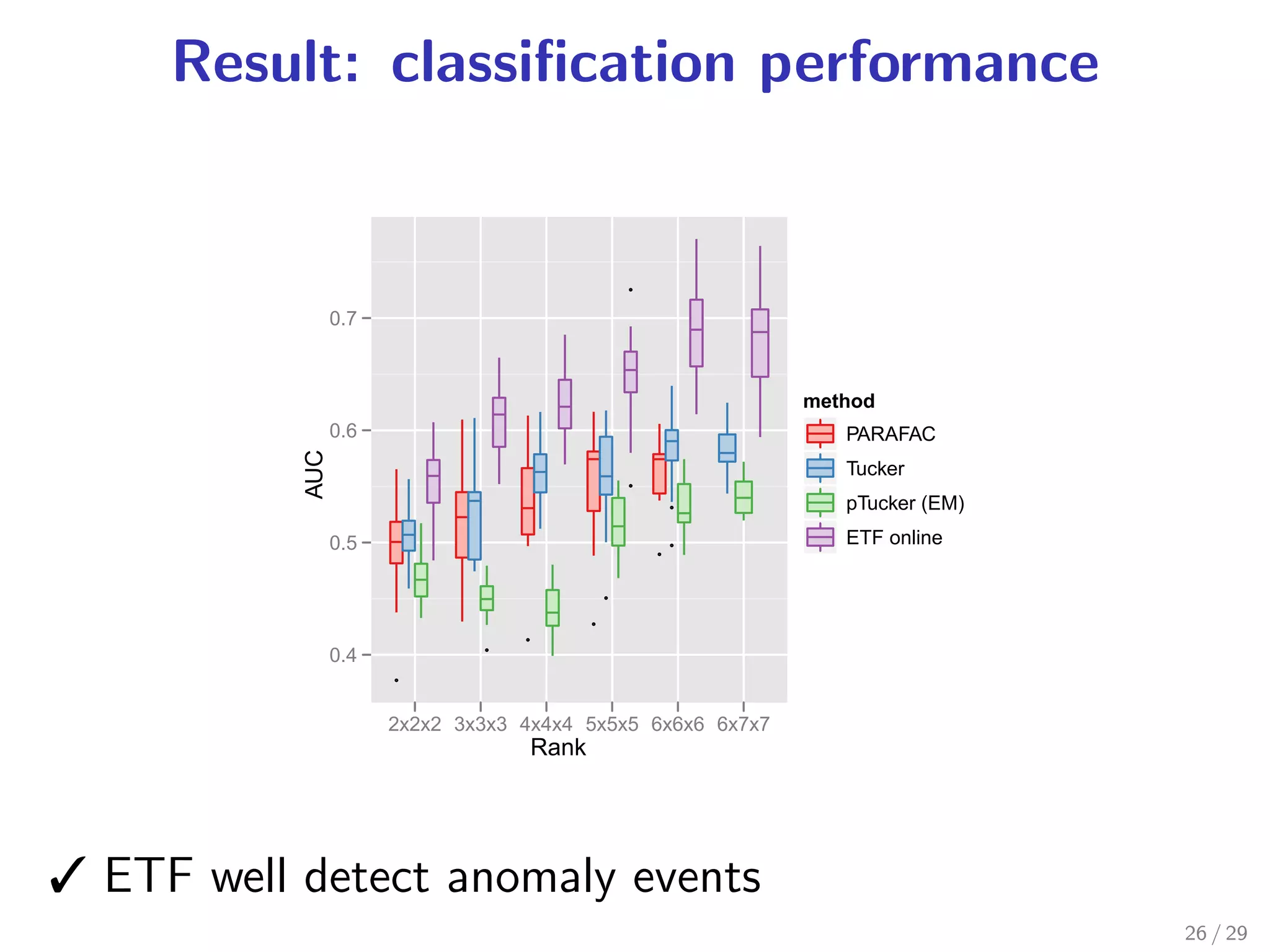
22. Anomaly detection by ETF
Purpose Find irregular parts of tensor data
Method Apply distance-based outlier
DB (p, D) [Knorr+ VLDB’00] to the estimated
factor matrix U(m)
.
Definition of DB (p, D)
.
“An object O is a DB (p, D) outlier if at least fraction p
. the objects lies at a distance greater than D from O.”
of
22 / 29

23. Data set
A time series of multisensor measurements
• Each sensor recorded the human behavior (e.g.
position) of researchers in NEC lab. for 8 month.
• 6 (sensors) × 21 (persons) × 1927 (hours)
Sensor Type Min Max
X1 # of sent emails Count 0.00 14.00
X2 # of received emails Count 0.00 15.00
X3 # of typed keys Count 0.00 50422.00
X4 X coordinate Real −550.17 3444.15
X5 Y coordinate Real 128.71 2353.55
X6 Movement distance Non-negative 0.00 203136.96
23 / 29

24. Evaluation
List of irregular events are provided.
Examples of irregular events
Date Time Description
Dec 21 All day Private incident
Dec 22 15:00 Monthly seminar
16:00
Jun 15 13:00 Visiting tour
.
. .
. .
.
. . .
• Evaluate as a binary classification
• 50% are missing, 10 trials
• Apply ETF with online algorithm
24 / 29

25. Result: classification performance
0.7
method
0.6 PARAFAC
AUC
Tucker
pTucker (EM)
0.5 ETF online
0.4
2x2x2 3x3x3 4x4x4 5x5x5 6x6x6 6x7x7
Rank
25 / 29

26. Result: classification performance
0.7
method
0.6 PARAFAC
AUC
Tucker
pTucker (EM)
0.5 ETF online
0.4
2x2x2 3x3x3 4x4x4 5x5x5 6x6x6 6x7x7
Rank
ETF well detect anomaly events
26 / 29

27. Skip the rest
27 / 29