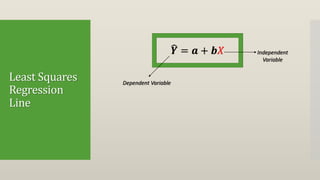
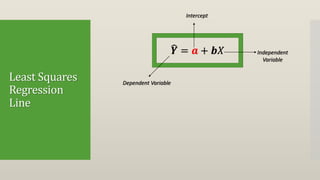
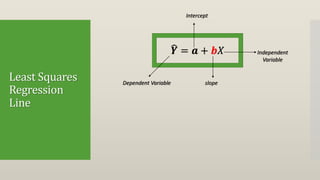
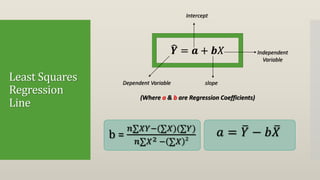
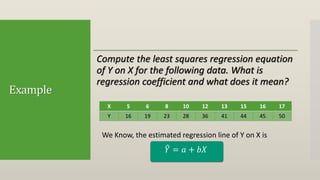
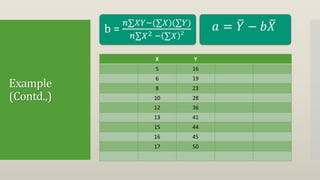
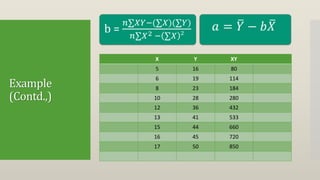
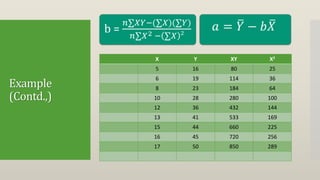
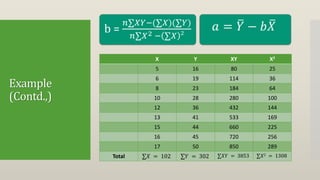
Regression attempts to model the relationship between a dependent variable (Y) and one or more independent variables (X). It provides an equation to estimate or predict the average value of Y based on the value(s) of X. The document then discusses single and multiple regression, the concept of a least squares regression line in the form of Y = a + bX, and provides an example to calculate the regression coefficients a and b and the regression line using a dataset with one dependent (Y) and independent (X) variable. The estimated regression line from the example is Y = 1.47 + 2.831X, where b=2.831 indicates that Y increases by 2.831 units for each one unit increase in X

1. Warda Iftikhar 13041519-014
Department of Computer Science
Regression
Presented to: Miss Madiha

2. Investopedia defines
Regression as ‘A statistical
measure that attempts to
determine the strength of
the relationship between
one dependent variable
(usually denoted by Y) and a
series of other changing
variables (known as
independent variables).’

3. Concept of
Regression
It investigates the dependence of one variable,
conventionally called the dependent variable, on one or
more other variables, called independent variables.
It then provides an equation to be used for estimating or
predicting the average value of the dependent variable
from the unknown values of the independent variable.
The relation between the expected value of the
dependent variable and the independent variable, is
called a regression relation.

4. Concept of
Regression
(Contd.)
The dependence of a variable on a single
independent variable, is called a single or two-
variable regression.
The dependence of a variable on two or more
independent variable, is called multiple
regression.
Regression is represented by a straight line
equation, and said to be linear regression.

5. Least Squares
Regression
Line
𝒀 = 𝒂 + 𝒃𝑿

6. Least Squares
Regression
Line
𝒀 = 𝒂 + 𝒃𝑿
Dependent Variable

7. Least Squares
Regression
Line
𝒀 = 𝒂 + 𝒃𝑋
Dependent Variable
Independent
Variable

8. Least Squares
Regression
Line
𝒀 = 𝒂 + 𝒃𝑋
Dependent Variable
Independent
Variable
Intercept

9. Least Squares
Regression
Line
𝒀 = 𝒂 + 𝒃𝑋
Dependent Variable
Independent
Variable
Intercept
slope

10. Least Squares
Regression
Line
𝒀 = 𝒂 + 𝒃𝑋
(Where a & b are Regression Coefficients)
Dependent Variable
Independent
Variable
Intercept
slope
b =
𝑛∑𝑋𝑌−(∑𝑋)(∑𝑌)
𝑛∑𝑋2 − ∑𝑋 2
𝑎 = 𝑌 − 𝑏 𝑋

11. Example
X 5 6 8 10 12 13 15 16 17
Y 16 19 23 28 36 41 44 45 50
Compute the least squares regression equation
of Y on X for the following data. What is
regression coefficient and what does it mean?
We Know, the estimated regression line of Y on X is
𝑌 = 𝑎 + 𝑏𝑋

12. Example
(Contd.,)
b =
𝑛∑𝑋𝑌−(∑𝑋)(∑𝑌)
𝑛∑𝑋2 − ∑𝑋 2
𝑎 = 𝑌 − 𝑏 𝑋
X Y
5 16
6 19
8 23
10 28
12 36
13 41
15 44
16 45
17 50

13. Example
(Contd.,)
b =
𝑛∑𝑋𝑌−(∑𝑋)(∑𝑌)
𝑛∑𝑋2 − ∑𝑋 2
𝑎 = 𝑌 − 𝑏 𝑋
X Y XY
5 16 80
6 19 114
8 23 184
10 28 280
12 36 432
13 41 533
15 44 660
16 45 720
17 50 850

14. Example
(Contd.,)
b =
𝑛∑𝑋𝑌−(∑𝑋)(∑𝑌)
𝑛∑𝑋2 − ∑𝑋 2
𝑎 = 𝑌 − 𝑏 𝑋
X Y XY X2
5 16 80 25
6 19 114 36
8 23 184 64
10 28 280 100
12 36 432 144
13 41 533 169
15 44 660 225
16 45 720 256
17 50 850 289

15. Example
(Contd.,)
b =
𝑛∑𝑋𝑌−(∑𝑋)(∑𝑌)
𝑛∑𝑋2 − ∑𝑋 2
𝑎 = 𝑌 − 𝑏 𝑋
X Y XY X2
5 16 80 25
6 19 114 36
8 23 184 64
10 28 280 100
12 36 432 144
13 41 533 169
15 44 660 225
16 45 720 256
17 50 850 289
Total ∑𝑋 = 102 ∑𝑌 = 302 ∑𝑋𝑌 = 3853 ∑𝑋2 = 1308

16. Example
(Contd.,)
b =
9 3853 − 102 (302)
9 1308 − 102 2

17. Example
(Contd.,)
b =
9 3853 − 102 (302)
9 1308 − 102 2
𝑏 =
34677 − 30804
11772 − 10404

18. Example
(Contd.,)
b =
9 3853 − 102 (302)
9 1308 − 102 2
𝑏 =
34677 − 30804
11772 −10404
𝑏 =
3873
1368
= 2.831

19. Example
(Contd.,)
b =
9 3853 − 102 (302)
9 1308 − 102 2
𝑏 =
34677 − 30804
11772 −10404
𝑏 =
3873
1368
= 2.831
𝑋 =
∑ 𝑋
𝑛
and 𝑌 =
∑ 𝑌
𝑛

20. Example
(Contd.,)
b =
9 3853 − 102 (302)
9 1308 − 102 2
𝑏 =
34677 − 30804
11772 −10404
𝑏 =
3873
1368
= 2.831
𝑋 =
∑ 𝑋
𝑛
and 𝑌 =
∑ 𝑌
𝑛
𝑋 =
102
9
and 𝑌 =
302
9

21. Example
(Contd.,)
b =
9 3853 − 102 (302)
9 1308 − 102 2
𝑏 =
34677 − 30804
11772 −10404
𝑏 =
3873
1368
= 2.831
𝑋 =
∑ 𝑋
𝑛
and 𝑌 =
∑ 𝑌
𝑛
𝑋 =
102
9
and 𝑌 =
302
9
𝑋 = 11.33 and 𝑌 = 33.56

22. Example
(Contd.,)
b =
9 3853 − 102 (302)
9 1308 − 102 2
𝑏 =
34677 − 30804
11772 −10404
𝑏 =
3873
1368
= 2.831
𝑋 =
∑ 𝑋
𝑛
and 𝑌 =
∑ 𝑌
𝑛
𝑋 =
102
9
and 𝑌 =
302
9
𝑋 = 11.33 and 𝑌 = 33.56
𝑎 = 33.56 − 2.831 11.33

23. Example
(Contd.,)
b =
9 3853 − 102 (302)
9 1308 − 102 2
𝑏 =
34677 − 30804
11772 −10404
𝑏 =
3873
1368
= 2.831
𝑋 =
∑ 𝑋
𝑛
and 𝑌 =
∑ 𝑌
𝑛
𝑋 =
102
9
and 𝑌 =
302
9
𝑋 = 11.33 and 𝑌 = 33.56
𝑎 = 33.56 − 2.831 11.33
𝑎 = 1.47

24. Example
(Contd.,)
b =
9 3853 − 102 (302)
9 1308 − 102 2
𝑏 =
34677 − 30804
11772 −10404
𝑏 =
3873
1368
= 2.831
𝑋 =
∑ 𝑋
𝑛
and 𝑌 =
∑ 𝑌
𝑛
𝑋 =
102
9
and 𝑌 =
302
9
𝑋 = 11.33 and 𝑌 = 33.56
𝑎 = 33.56 − 2.831 11.33
𝑎 = 1.47
Hence the desired estimated regression line of Y on X is
𝑌 = 1.47 + 2.831𝑋

25. The estimated regression co-
efficient, 𝑏 = 2.831, which indicates
that the values of Y increase by
2.831 units for a unit increase in X.

26. THAT’S ALL…
QUESTIONS??