Uploaded byankit_ppt
PPTX, PDF256 views

Ml6 decision trees

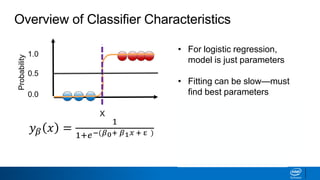
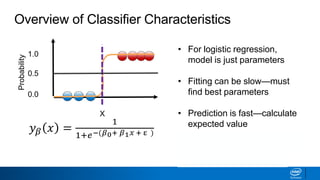
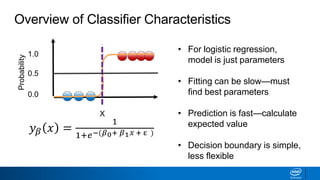
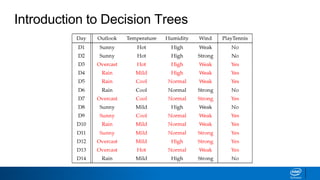
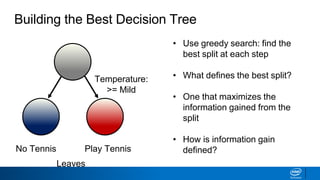
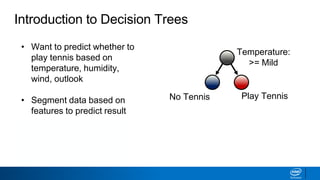
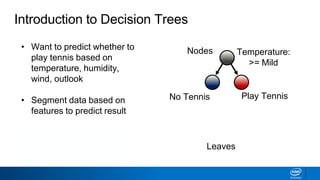
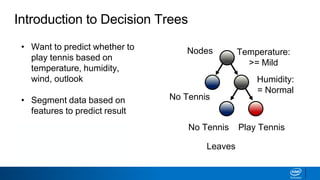
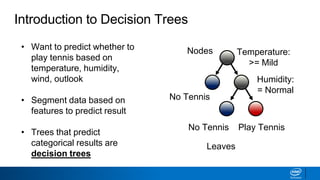
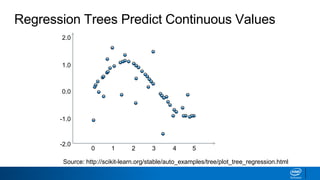
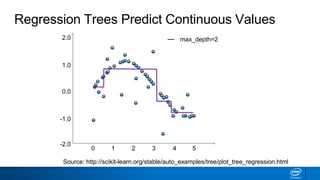
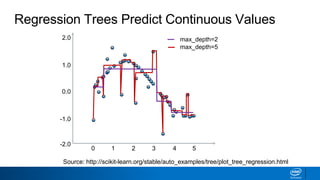
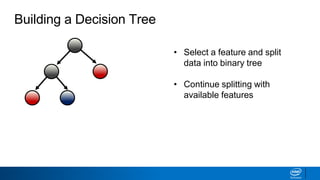
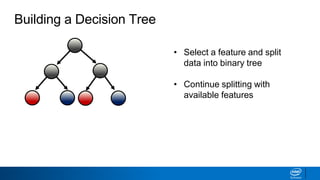
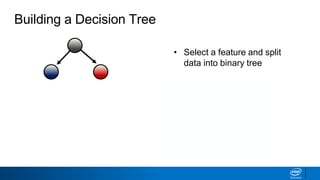
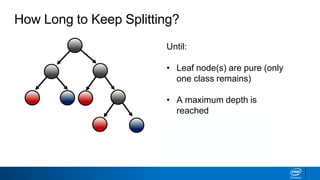
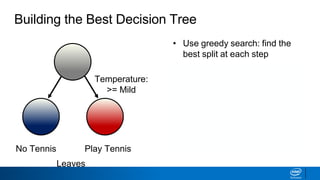
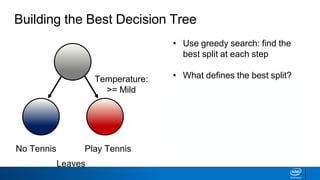
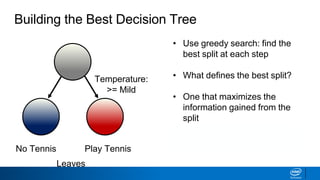
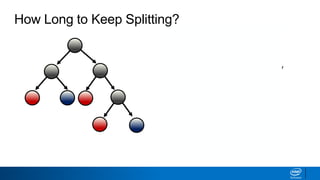
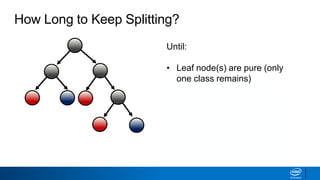
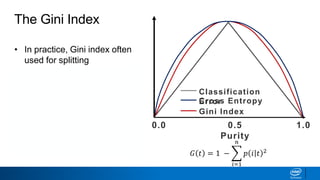
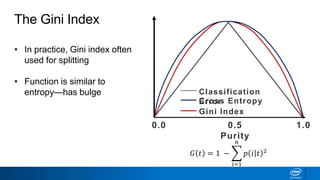
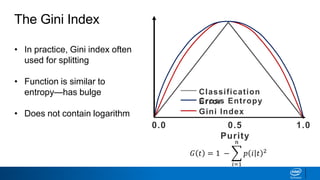
The document provides an overview of decision trees, including: - Decision trees can be used for classification or regression problems by segmenting data based on features to predict categorical or continuous target values. - The tree is built recursively by selecting the best feature to split the data on at each node, with the goal of maximizing information gain or minimizing entropy. - Splits continue until nodes are pure or a stopping criteria like maximum depth is reached. Entropy works better than classification error as a splitting metric because it favors splits furthest from ambiguous 50/50 splits.

Embed presentation

Downloaded 33 times
Decision Trees
Legal Notices and Disclaimers This presentation is for informational purposes only. INTEL MAKES NO WARRANTIES, EXPRESS OR IMPLIED, IN THIS SUMMARY. Intel technologies’ features and benefits depend on system configuration and may require enabled hardware, software or service activation. Performance varies depending on system configuration. Check with your system manufacturer or retailer or learn more at intel.com. This sample source code is released under the Intel Sample Source Code License Agreement. Intel and the Intel logo are trademarks of Intel Corporation in the U.S. and/or other countries. *Other names and brands may be claimed as the property of others. Copyright © 2017, Intel Corporation. All rights reserved.
Overview of Classifier Characteristics X Y • For K-Nearest Neighbors, training data is the model • Fitting is fast—just store data • Prediction can be slow—lots of distances to measure • Decision boundary is flexible
Overview of Classifier Characteristics X Y • For K-Nearest Neighbors, training data is the model • Fitting is fast—just store data • Prediction can be slow—lots of distances to measure • Decision boundary is flexible
Overview of Classifier Characteristics X Y • For K-Nearest Neighbors, training data is the model • Fitting is fast—just store data • Prediction can be slow—lots of distances to measure • Decision boundary is flexible
Overview of Classifier Characteristics X Y • For K-Nearest Neighbors, training data is the model • Fitting is fast—just store data • Prediction can be slow—lots of distances to measure • Decision boundary is flexible
X 0.0 1.0 Probability 0.5 𝑦 𝛽 𝑥 = 1 1+𝑒−(𝛽0+ 𝛽1 𝑥 + ε ) Overview of Classifier Characteristics • For logistic regression, model is just parameters • Fitting can be slow—must find best parameters • Prediction is fast—calculate expected value • Decision boundary is simple, less flexible
X 0.0 1.0 Probability 0.5 𝑦 𝛽 𝑥 = 1 1+𝑒−(𝛽0+ 𝛽1 𝑥 + ε ) Overview of Classifier Characteristics • For logistic regression, model is just parameters • Fitting can be slow—must find best parameters • Prediction is fast—calculate expected value • Decision boundary is simple, less flexible
X 0.0 1.0 Probability 0.5 𝑦 𝛽 𝑥 = 1 1+𝑒−(𝛽0+ 𝛽1 𝑥 + ε ) Overview of Classifier Characteristics • For logistic regression, model is just parameters • Fitting can be slow—must find best parameters • Prediction is fast—calculate expected value • Decision boundary is simple, less flexible
X 0.0 1.0 Probability 0.5 𝑦 𝛽 𝑥 = 1 1+𝑒−(𝛽0+ 𝛽1 𝑥 + ε ) Overview of Classifier Characteristics • For logistic regression, model is just parameters • Fitting can be slow—must find best parameters • Prediction is fast—calculate expected value • Decision boundary is simple, less flexible
Introduction to Decision Trees
Introduction to Decision Trees • Want to predict whether to play tennis based on temperature, humidity, wind, outlook • Segment data based on features to predict result • Trees that predict categorical results are decision trees
Introduction to Decision Trees • Want to predict whether to play tennis based on temperature, humidity, wind, outlook • Segment data based on features to predict result • Trees that predict categorical results are decision trees Temperature: >= Mild Play TennisNo Tennis
Play Tennis Nodes Introduction to Decision Trees • Want to predict whether to play tennis based on temperature, humidity, wind, outlook • Segment data based on features to predict result • Trees that predict categorical results are decision trees Leaves Temperature: >= Mild No Tennis
Play TennisNo Tennis Nodes Leaves No Tennis Humidity: = Normal Introduction to Decision Trees • Want to predict whether to play tennis based on temperature, humidity, wind, outlook • Segment data based on features to predict result • Trees that predict categorical results are decision trees Temperature: >= Mild
Play TennisNo Tennis Nodes Leaves • Want to predict whether to play tennis based on temperature, humidity, wind, outlook • Segment data based on features to predict result • Trees that predict categorical results are decision trees No Tennis Introduction to Decision Trees Temperature: >= Mild Humidity: = Normal
• Example: use slope an elevation in Himalayas • Predict average precipitation (continuous value) Regression Trees Predict Continuous Values
48.50 in.13.67 in. Nodes Leaves Elevation: < 7900 ft. 55.42 in. Slope: < 2.5º Regression Trees Predict Continuous Values • Example: use slope an elevation in Himalayas • Predict average precipitation (continuous value)
48.50 in.13.67 in. Nodes Leaves Elevation: < 7900 ft. • Example: use slope an elevation in Himalayas • Predict average precipitation (continuous value) • Values at leaves are averages of members 55.42 in. Slope: < 2.5º Regression Trees Predict Continuous Values
Regression Trees Predict Continuous Values 0 1 2 3 4 5 -1.0 -2.0 0.0 1.0 2.0 Source: http://scikit-learn.org/stable/auto_examples/tree/plot_tree_regression.html
Regression Trees Predict Continuous Values max_depth=2 0 1 2 3 4 5 -1.0 -2.0 0.0 1.0 2.0 Source: http://scikit-learn.org/stable/auto_examples/tree/plot_tree_regression.html
Regression Trees Predict Continuous Values max_depth=2 max_depth=5 0 1 2 3 4 5 -1.0 -2.0 0.0 1.0 2.0 Source: http://scikit-learn.org/stable/auto_examples/tree/plot_tree_regression.html
Building a Decision Tree • Select a feature and split data into binary tree • Continue splitting with available features
Building a Decision Tree • Select a feature and split data into binary tree • Continue splitting with available features
Building a Decision Tree • Select a feature and split data into binary tree • Continue splitting with available features
How Long to Keep Splitting? Until: • Leaf node(s) are pure (only one class remains) • A maximum depth is reached • A performance metric is achieved
How Long to Keep Splitting? Until: • Leaf node(s) are pure (only one class remains) • A maximum depth is reached • A performance metric is achieved
How Long to Keep Splitting? Until: • Leaf node(s) are pure (only one class remains) • A maximum depth is reached • A performance metric is achieved
How Long to Keep Splitting? Until: • Leaf node(s) are pure—only one class remains • A maximum depth is reached • A performance metric is achieved
• Use greedy search: find the best split at each step • What defines the best split? • One that maximizes the information gained from the split • How is information gain defined? Building the Best Decision Tree Play Tennis Leaves No Tennis Temperature: >= Mild
• Use greedy search: find the best split at each step • What defines the best split? • One that maximizes the information gained from the split • How is information gain defined? Building the Best Decision Tree Play Tennis Leaves No Tennis Temperature: >= Mild
• Use greedy search: find the best split at each step • What defines the best split? • One that maximizes the information gained from the split • How is information gain defined? Building the Best Decision Tree Play Tennis Leaves No Tennis Temperature: >= Mild
• Use greedy search: find the best split at each step • What defines the best split? • One that maximizes the information gained from the split • How is information gain defined? Building the Best Decision Tree Play Tennis Leaves No Tennis Temperature: >= Mild
Splitting Based on Classification Error 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ] Classification Error Equation Classification Error Before 1 − 8 12 = 0.3333
Splitting Based on Classification Error 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ] Classification Error Equation Classification Error Before 1 − 8 12 = 0.3333
Splitting Based on Classification Error 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ] Classification Error Equation Classification Error Left Side 1 − 2 4 = 0.5000 0.3333
Splitting Based on Classification Error 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ] Classification Error Equation Classification Error Left Side 1 − 2 4 = 0.5000 0.3333 Information lost on small # of data points
Splitting Based on Classification Error 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ] Classification Error Equation Classification Error Right Side 1 − 6 8 = 0.2500 0.3333 0.5000
Splitting Based on Classification Error 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ] Classification Error Equation Classification Error Change 0.3333 − 4 12 ∗ 0.5000 − 8 12 ∗0.2500 = 0 0.3333 0.5000 0.2500
Splitting Based on Classification Error 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ] Classification Error Equation Classification Error Change 0.3333 0.5000 0.2500 0.3333 − 4 12 ∗ 0.5000 − 8 12 ∗0.2500 = 0
Splitting Based on Classification Error 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No • Using classification error, no further splits would occur • Problem: end nodes are not homogeneous • Try a different metric?
Splitting Based on Entropy 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐻 𝑡 = − 𝑖=1 𝑛 𝑝 𝑖 𝑡 𝑙𝑜𝑔2[𝑝(𝑖|𝑡)] Entropy Equation Entropy Before − 8 12 𝑙𝑜𝑔2(8 12) − 4 12 𝑙𝑜𝑔2(4 12) = 0.9183
Splitting Based on Entropy 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐻 𝑡 = − 𝑖=1 𝑛 𝑝 𝑖 𝑡 𝑙𝑜𝑔2[𝑝(𝑖|𝑡)] Entropy Equation Entropy Before − 8 12 𝑙𝑜𝑔2(8 12) − 4 12 𝑙𝑜𝑔2(4 12) = 0.9183
Splitting Based on Entropy 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐻 𝑡 = − 𝑖=1 𝑛 𝑝 𝑖 𝑡 𝑙𝑜𝑔2[𝑝(𝑖|𝑡)] Entropy Equation Entropy Left Side − 2 4 𝑙𝑜𝑔2(2 4) − 2 4 𝑙𝑜𝑔2(2 4) = 1.0000 0.9183
Splitting Based on Entropy 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐻 𝑡 = − 𝑖=1 𝑛 𝑝 𝑖 𝑡 𝑙𝑜𝑔2[𝑝(𝑖|𝑡)] Entropy Equation Entropy Right Side − 6 8 𝑙𝑜𝑔2(6 8) − 2 8 𝑙𝑜𝑔2(2 8) = 0.8113 0.9183 1.0000
Splitting Based on Entropy 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐻 𝑡 = − 𝑖=1 𝑛 𝑝 𝑖 𝑡 𝑙𝑜𝑔2[𝑝(𝑖|𝑡)] Entropy Equation Entropy Change 0.9183 − 4 12 ∗ 1.0000 − 8 12 ∗0.8113 = 0.0441 0.9183 1.0000 0.8113
Splitting Based on Entropy 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No • Splitting based on entropy allows further splits to occur • Can eventually reach goal of homogeneous nodes • Why does this work with entropy but not classification error?
Splitting Based on Entropy 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No • Splitting based on entropy allows further splits to occur • Can eventually reach goal of homogeneous nodes • Why does this work with entropy but not classification error?
Splitting Based on Entropy 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No • Splitting based on entropy allows further splits to occur • Can eventually reach goal of homogeneous nodes • Why does this work with entropy but not classification error?
• Classification error is a flat function with maximum at center • Center represents ambiguity—50/50 split • Splitting metrics favor results that are furthest away from the center Classification Error vs Entropy 0.0 0.5 Purity 1.0 Classification Error 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ] Error
• Classification error is a flat function with maximum at center • Center represents ambiguity—50/50 split • Splitting metrics favor results that are furthest away from the center Classification Error vs Entropy 0.0 0.5 Purity 1.0 Classification Error 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ] Error
0.0 0.5 Purity 1.0 Classification Error • Classification error is a flat function with maximum at center • Center represents ambiguity—50/50 split • Splitting metrics favor results that are furthest away from the center 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ] Classification Error vs Entropy Error
Classification Error vs Entropy • Entropy has the same maximum but is curved • Curvature allows splitting to continue until nodes are pure • How does this work? 0.0 0.5 Purity 1.0 Classification ErrorCross Entropy 𝐻 𝑡 = − 𝑖=1 𝑛 𝑝 𝑖 𝑡 𝑙𝑜𝑔2[𝑝(𝑖|𝑡)] Error/Entropy
Classification Error vs Entropy • Entropy has the same maximum but is curved • Curvature allows splitting to continue until nodes are pure • How does this work? 0.0 0.5 Purity 1.0 Classification ErrorCross Entropy 𝐻 𝑡 = − 𝑖=1 𝑛 𝑝 𝑖 𝑡 𝑙𝑜𝑔2[𝑝(𝑖|𝑡)] Error/Entropy
0.0 0.5 Purity 1.0 Classification ErrorCross Entropy Classification Error vs Entropy • Entropy has the same maximum but is curved • Curvature allows splitting to continue until nodes are pure • How does this work? 𝐻 𝑡 = − 𝑖=1 𝑛 𝑝 𝑖 𝑡 𝑙𝑜𝑔2[𝑝(𝑖|𝑡)] Error/Entropy
Information Gained by Splitting • With classification error, the function is flat • Final average classification error can be identical to parent • Resulting in premature stopping
Information Gained by Splitting • With classification error, the function is flat • Final average classification error can be identical to parent • Resulting in premature stopping
Information Gained by Splitting • With classification error, the function is flat • Final average classification error can be identical to parent • Resulting in premature stopping
Information Gained by Splitting • With classification error, the function is flat • Final average classification error can be identical to parent • Resulting in premature stopping
Information Gained by Splitting • With entropy gain, the function has a "bulge" • Allows average information of children to be less than parent • Results in information gain and continued splitting
Information Gained by Splitting • With entropy gain, the function has a "bulge" • Allows average information of children to be less than parent • Results in information gain and continued splitting
Information Gained by Splitting • With entropy gain, the function has a "bulge" • Allows average information of children to be less than parent • Results in information gain and continued splitting
0.0 0.5 Purity 1.0 Classification ErrorCross Entropy Gini Index • In practice, Gini index often used for splitting • Function is similar to entropy—has bulge • Does not contain logarithm The Gini Index 𝐺 𝑡 = 1 − 𝑖=1 𝑛 𝑝 𝑖 𝑡 2
0.0 0.5 Purity 1.0 Classification ErrorCross Entropy Gini Index • In practice, Gini index often used for splitting • Function is similar to entropy—has bulge • Does not contain logarithm The Gini Index 𝐺 𝑡 = 1 − 𝑖=1 𝑛 𝑝 𝑖 𝑡 2
0.0 0.5 Purity 1.0 Classification ErrorCross Entropy Gini Index • In practice, Gini index often used for splitting • Function is similar to entropy—has bulge • Does not contain logarithm The Gini Index 𝐺 𝑡 = 1 − 𝑖=1 𝑛 𝑝 𝑖 𝑡 2
Decision Trees are High Variance • Problem: decision trees tend to overfit • Small changes in data greatly affect prediction-- high variance • Solution: Prune trees
• Problem: decision trees tend to overfit • Small changes in data greatly affect prediction-- high variance • Solution: Prune trees Decision Trees are High Variance
• Problem: decision trees tend to overfit • Small changes in data greatly affect prediction-- high variance • Solution: Prune trees Decision Trees are High Variance
Pruning Decision Trees • Problem: decision trees tend to overfit • Small changes in data greatly affect prediction-- high variance • Solution: Prune trees
Pruning Decision Trees • Problem: decision trees tend to overfit • Small changes in data greatly affect prediction-- high variance • Solution: Prune trees
• How to decide what leaves to prune? • Solution: prune based on classification error threshold Pruning Decision Trees
• How to decide what leaves to prune? • Solution: prune based on classification error threshold Pruning Decision Trees 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ]
• Easy to interpret and implement—"if … then … else" logic • Handle any data category— binary, ordinal, continuous • No preprocessing or scaling required Strengths of Decision Trees
• Easy to interpret and implement—"if … then … else" logic • Handle any data category— binary, ordinal, continuous • No preprocessing or scaling required Strengths of Decision Trees
• Easy to interpret and implement—"if … then … else" logic • Handle any data category— binary, ordinal, continuous • No preprocessing or scaling required Strengths of Decision Trees
Import the class containing the classification method from sklearn.tree import DecisionTreeClassifier Create an instance of the class DTC = DecisionTreeClassifier(criterion='gini', max_features=10, max_depth=5) Fit the instance on the data and then predict the expected value DTC = DTC.fit(X_train, y_train) y_predict = DTC.predict(X_test) Tune parameters with cross-validation. Use DecisionTreeRegressor for regression. DecisionTreeClassifier: The Syntax
Import the class containing the classification method from sklearn.tree import DecisionTreeClassifier Create an instance of the class DTC = DecisionTreeClassifier(criterion='gini', max_features=10, max_depth=5) Fit the instance on the data and then predict the expected value DTC = DTC.fit(X_train, y_train) y_predict = DTC.predict(X_test) Tune parameters with cross-validation. Use DecisionTreeRegressor for regression. DecisionTreeClassifier: The Syntax
Import the class containing the classification method from sklearn.tree import DecisionTreeClassifier Create an instance of the class DTC = DecisionTreeClassifier(criterion='gini', max_features=10, max_depth=5) Fit the instance on the data and then predict the expected value DTC = DTC.fit(X_train, y_train) y_predict = DTC.predict(X_test) Tune parameters with cross-validation. Use DecisionTreeRegressor for regression. DecisionTreeClassifier: The Syntax tree parameters
Import the class containing the classification method from sklearn.tree import DecisionTreeClassifier Create an instance of the class DTC = DecisionTreeClassifier(criterion='gini', max_features=10, max_depth=5) Fit the instance on the data and then predict the expected value DTC = DTC.fit(X_train, y_train) y_predict = DTC.predict(X_test) Tune parameters with cross-validation. Use DecisionTreeRegressor for regression. DecisionTreeClassifier: The Syntax
DecisionTreeClassifier: The Syntax Import the class containing the classification method from sklearn.tree import DecisionTreeClassifier Create an instance of the class DTC = DecisionTreeClassifier(criterion='gini', max_features=10, max_depth=5) Fit the instance on the data and then predict the expected value DTC = DTC.fit(X_train, y_train) y_predict = DTC.predict(X_test) Tune parameters with cross-validation. Use DecisionTreeRegressor for regression.
Ml6 decision trees

More Related Content

PPTX
Ml4 naive bayes
byankit_ppt
 
PPTX
Ml8 boosting and-stacking
byankit_ppt
 
PPTX
Ml7 bagging
byankit_ppt
 
PPTX
Ml9 introduction to-unsupervised_learning_and_clustering_methods
byankit_ppt
 
PPTX
Machine learning and_nlp
byankit_ppt
 
PPTX
Ml2 train test-splits_validation_linear_regression
byankit_ppt
 
PDF
ICCV2013 reading: Learning to rank using privileged information
byAkisato Kimura
 
PPTX
Gradient Boosted trees
byNihar Ranjan
 
Ml4 naive bayes
byankit_ppt
 
Ml8 boosting and-stacking
byankit_ppt
 
Ml7 bagging
byankit_ppt
 
Ml9 introduction to-unsupervised_learning_and_clustering_methods
byankit_ppt
 
Machine learning and_nlp
byankit_ppt
 
Ml2 train test-splits_validation_linear_regression
byankit_ppt
 
ICCV2013 reading: Learning to rank using privileged information
byAkisato Kimura
 
Gradient Boosted trees
byNihar Ranjan
 

What's hot

PDF
CVPR2015 reading "Global refinement of random forest"
byAkisato Kimura
 
PPTX
Decision trees for machine learning
byAmr BARAKAT
 
PPT
Slide3.ppt
bybutest
 
PPTX
08 neural networks
byankit_ppt
 
PPTX
Ml10 dimensionality reduction-and_advanced_topics
byankit_ppt
 
PPT
Machine Learning 3 - Decision Tree Learning
bybutest
 
PDF
Random forest sgv_ai_talk_oct_2_2018
bydigitalzombie
 
PDF
Jan vitek distributedrandomforest_5-2-2013
bySri Ambati
 
PPTX
ID3 ALGORITHM
byHARDIK SINGH
 
PPTX
Classification Continued
byDataminingTools Inc
 
PPTX
Classification decision tree
byyazad dumasia
 
PDF
L3. Decision Trees
byMachine Learning Valencia
 
PDF
GBM theory code and parameters
byVenkata Reddy Konasani
 
PPTX
Comparison Study of Decision Tree Ensembles for Regression
bySeonho Park
 
PPTX
WEKA: Algorithms The Basic Methods
byDataminingTools Inc
 
PDF
Decision tree
byR A Akerkar
 
PPTX
Ppt shuai
byXiang Zhang
 
PDF
Kaggle Higgs Boson Machine Learning Challenge
byBernard Ong
 
PPT
Covering (Rules-based) Algorithm
byZHAO Sam
 
PPTX
Random Forest and KNN is fun
byZhen Li
 
CVPR2015 reading "Global refinement of random forest"
byAkisato Kimura
 
Decision trees for machine learning
byAmr BARAKAT
 
Slide3.ppt
bybutest
 
08 neural networks
byankit_ppt
 
Ml10 dimensionality reduction-and_advanced_topics
byankit_ppt
 
Machine Learning 3 - Decision Tree Learning
bybutest
 
Random forest sgv_ai_talk_oct_2_2018
bydigitalzombie
 
Jan vitek distributedrandomforest_5-2-2013
bySri Ambati
 
ID3 ALGORITHM
byHARDIK SINGH
 
Classification Continued
byDataminingTools Inc
 
Classification decision tree
byyazad dumasia
 
L3. Decision Trees
byMachine Learning Valencia
 
GBM theory code and parameters
byVenkata Reddy Konasani
 
Comparison Study of Decision Tree Ensembles for Regression
bySeonho Park
 
WEKA: Algorithms The Basic Methods
byDataminingTools Inc
 
Decision tree
byR A Akerkar
 
Ppt shuai
byXiang Zhang
 
Kaggle Higgs Boson Machine Learning Challenge
byBernard Ong
 
Covering (Rules-based) Algorithm
byZHAO Sam
 
Random Forest and KNN is fun
byZhen Li
 

Similar to Ml6 decision trees

PDF
Aiml ajsjdjcjcjcjfjfjModule4_Pashrt1-1.pdf
byCHIRAGGOWDA41
 
PPT
introduction to machine learning 3c.pptx
byPratik Gohel
 
PPT
machine learning.ppt
byPratik Gohel
 
DOCX
Classification Using Decision Trees and RulesChapter 5.docx
bymonicafrancis71118
 
PPTX
Decision Trees Learning in Machine Learning
bySenthil Vit
 
PDF
CSA 3702 machine learning module 2
byNandhini S
 
PDF
From decision trees to random forests
byViet-Trung TRAN
 
PPT
Decision Trees.ppt
bymuhammadabdullah400131
 
PPT
DecisionTrees_ID3_RandomForest_Combined.ppt
byssuser591bd21
 
PDF
Decision Tree in classification problems in ML
by22054561
 
PPTX
Lect9 Decision tree
byhktripathy
 
PDF
Decision trees
byNcib Lotfi
 
PDF
Decision treeDecision treeDecision treeDecision tree
bySsdSsd5
 
PDF
Decision Tree-ID3,C4.5,CART,Regression Tree
bySharmila Chidaravalli
 
PPTX
Linear Regression and Decision Trees.pptx
byrajab ssemwogerere
 
PPTX
3. Tree Models in machine learning
byKv Sagar
 
PPTX
BAS 250 Lecture 8
byWake Tech BAS
 
PDF
Nhan_Chapter 6_Classification 2022.pdf
byNhtHong96
 
PDF
Decision tree learning
byDr. Radhey Shyam
 
PPTX
machine learning decision tree algorithm
bymustaq4
 
Aiml ajsjdjcjcjcjfjfjModule4_Pashrt1-1.pdf
byCHIRAGGOWDA41
 
introduction to machine learning 3c.pptx
byPratik Gohel
 
machine learning.ppt
byPratik Gohel
 
Classification Using Decision Trees and RulesChapter 5.docx
bymonicafrancis71118
 
Decision Trees Learning in Machine Learning
bySenthil Vit
 
CSA 3702 machine learning module 2
byNandhini S
 
From decision trees to random forests
byViet-Trung TRAN
 
Decision Trees.ppt
bymuhammadabdullah400131
 
DecisionTrees_ID3_RandomForest_Combined.ppt
byssuser591bd21
 
Decision Tree in classification problems in ML
by22054561
 
Lect9 Decision tree
byhktripathy
 
Decision trees
byNcib Lotfi
 
Decision treeDecision treeDecision treeDecision tree
bySsdSsd5
 
Decision Tree-ID3,C4.5,CART,Regression Tree
bySharmila Chidaravalli
 
Linear Regression and Decision Trees.pptx
byrajab ssemwogerere
 
3. Tree Models in machine learning
byKv Sagar
 
BAS 250 Lecture 8
byWake Tech BAS
 
Nhan_Chapter 6_Classification 2022.pdf
byNhtHong96
 
Decision tree learning
byDr. Radhey Shyam
 
machine learning decision tree algorithm
bymustaq4
 

More from ankit_ppt

PPTX
Deep learning summary
byankit_ppt
 
PPTX
07 learning
byankit_ppt
 
PPTX
06 image features
byankit_ppt
 
PPTX
05 contours seg_matching
byankit_ppt
 
PPTX
04 image transformations_ii
byankit_ppt
 
PPTX
03 image transformations_i
byankit_ppt
 
PPTX
02 image processing
byankit_ppt
 
PPTX
01 foundations
byankit_ppt
 
PPTX
Word2 vec
byankit_ppt
 
PPTX
Text similarity measures
byankit_ppt
 
PPTX
Text generation and_advanced_topics
byankit_ppt
 
PPTX
Nlp toolkits and_preprocessing_techniques
byankit_ppt
 
PPTX
Matrix decomposition and_applications_to_nlp
byankit_ppt
 
PPTX
Latent dirichlet allocation_and_topic_modeling
byankit_ppt
 
PPTX
Intro to nlp
byankit_ppt
 
PPTX
Ot regularization and_gradient_descent
byankit_ppt
 
PPTX
Ml5 svm and-kernels
byankit_ppt
 
PPTX
Lesson 3 ai in the enterprise
byankit_ppt
 
PPTX
Ml3 logistic regression-and_classification_error_metrics
byankit_ppt
 
PPTX
Ml1 introduction to-supervised_learning_and_k_nearest_neighbors
byankit_ppt
 
Deep learning summary
byankit_ppt
 
07 learning
byankit_ppt
 
06 image features
byankit_ppt
 
05 contours seg_matching
byankit_ppt
 
04 image transformations_ii
byankit_ppt
 
03 image transformations_i
byankit_ppt
 
02 image processing
byankit_ppt
 
01 foundations
byankit_ppt
 
Word2 vec
byankit_ppt
 
Text similarity measures
byankit_ppt
 
Text generation and_advanced_topics
byankit_ppt
 
Nlp toolkits and_preprocessing_techniques
byankit_ppt
 
Matrix decomposition and_applications_to_nlp
byankit_ppt
 
Latent dirichlet allocation_and_topic_modeling
byankit_ppt
 
Intro to nlp
byankit_ppt
 
Ot regularization and_gradient_descent
byankit_ppt
 
Ml5 svm and-kernels
byankit_ppt
 
Lesson 3 ai in the enterprise
byankit_ppt
 
Ml3 logistic regression-and_classification_error_metrics
byankit_ppt
 
Ml1 introduction to-supervised_learning_and_k_nearest_neighbors
byankit_ppt
 

Recently uploaded

PPTX
We-Optimized-Everything-Except-Decision-Quality-Maintenance-MaintWiz.pptx
byMaintWiz Technologies Private Limited
 
PPTX
Origin of Soil and Grain Size with Introduction and explanation
byMahmoodKhalid11
 
PPT
Introduction to Concord Decorator by Stolle.ppt
bymorachatgpt123
 
PDF
TechRush Hackathon 2026: A Platform for Innovation, Learning, and Real-World ...
byreshmi7103
 
PPTX
WOWVerse Workshop: Agentic AI & LLM Workshop
byram27belitkar
 
PDF
ERTMS-conference-WS8_Presentations_v0.pdf
byEduardo147194
 
PPTX
Using Bangladesh studies in cse why matter ppp.pptx
bymsprinceahmedontor40
 
PPTX
Basin Design Service, LLC Introduction Presentation
byHubie Fix
 
PPTX
Theory to Practice of Unsaturated Soil Mechanics-1.pptx
byMahmoodKhalid11
 
PDF
God series - Physics video office crossed
byjangidankit8781
 
PDF
comprehensive analysis of cross-chain bridges in the DeFi - Garima Singh
byGarima Singh
 
PDF
Chip Designer's Code - Linux Terminal Part 7.1 - Text Processing
byAmr Adel
 
PPTX
Electronics Device - EC25C01 - Semiconductor: Types, Conductivity,
byMathavan N
 
PDF
0.39 Inch Micro-OLED Display 1024×768 XGA Panel Silicon OLED
bySyluxdisplay
 
PPTX
Top 3 winning teams announcement - TechSprint
bybajpaitusharoffon678
 
PPTX
Concord Deco Training by Stolle- Safety.pptx
bymorachatgpt123
 
PPTX
TELECOMMUNICATION FOR SOCIETY to all over
bymadagonikranthikumar
 
PPTX
Optimized access control techniques in Cloud Computing with Security and Scal...
bymareswariesteru
 
PPTX
UNIT 2 _8051.pptx ,INSTRUCTION SET OF 8051,EXAMPLES OF ARITHMETIC,LOGICAL.BRA...
byrekhabalaji2607
 
PDF
5.5 Inch 4K TFT LCD Display 3840×2160 UHD Panel – LS055D1SX05(G)
bySyluxdisplay
 
We-Optimized-Everything-Except-Decision-Quality-Maintenance-MaintWiz.pptx
byMaintWiz Technologies Private Limited
 
Origin of Soil and Grain Size with Introduction and explanation
byMahmoodKhalid11
 
Introduction to Concord Decorator by Stolle.ppt
bymorachatgpt123
 
TechRush Hackathon 2026: A Platform for Innovation, Learning, and Real-World ...
byreshmi7103
 
WOWVerse Workshop: Agentic AI & LLM Workshop
byram27belitkar
 
ERTMS-conference-WS8_Presentations_v0.pdf
byEduardo147194
 
Using Bangladesh studies in cse why matter ppp.pptx
bymsprinceahmedontor40
 
Basin Design Service, LLC Introduction Presentation
byHubie Fix
 
Theory to Practice of Unsaturated Soil Mechanics-1.pptx
byMahmoodKhalid11
 
God series - Physics video office crossed
byjangidankit8781
 
comprehensive analysis of cross-chain bridges in the DeFi - Garima Singh
byGarima Singh
 
Chip Designer's Code - Linux Terminal Part 7.1 - Text Processing
byAmr Adel
 
Electronics Device - EC25C01 - Semiconductor: Types, Conductivity,
byMathavan N
 
0.39 Inch Micro-OLED Display 1024×768 XGA Panel Silicon OLED
bySyluxdisplay
 
Top 3 winning teams announcement - TechSprint
bybajpaitusharoffon678
 
Concord Deco Training by Stolle- Safety.pptx
bymorachatgpt123
 
TELECOMMUNICATION FOR SOCIETY to all over
bymadagonikranthikumar
 
Optimized access control techniques in Cloud Computing with Security and Scal...
bymareswariesteru
 
UNIT 2 _8051.pptx ,INSTRUCTION SET OF 8051,EXAMPLES OF ARITHMETIC,LOGICAL.BRA...
byrekhabalaji2607
 
5.5 Inch 4K TFT LCD Display 3840×2160 UHD Panel – LS055D1SX05(G)
bySyluxdisplay
 

Ml6 decision trees

  • 1.
  • 2.
    Legal Notices andDisclaimers This presentation is for informational purposes only. INTEL MAKES NO WARRANTIES, EXPRESS OR IMPLIED, IN THIS SUMMARY. Intel technologies’ features and benefits depend on system configuration and may require enabled hardware, software or service activation. Performance varies depending on system configuration. Check with your system manufacturer or retailer or learn more at intel.com. This sample source code is released under the Intel Sample Source Code License Agreement. Intel and the Intel logo are trademarks of Intel Corporation in the U.S. and/or other countries. *Other names and brands may be claimed as the property of others. Copyright © 2017, Intel Corporation. All rights reserved.
  • 3.
    Overview of ClassifierCharacteristics X Y • For K-Nearest Neighbors, training data is the model • Fitting is fast—just store data • Prediction can be slow—lots of distances to measure • Decision boundary is flexible
  • 4.
    Overview of ClassifierCharacteristics X Y • For K-Nearest Neighbors, training data is the model • Fitting is fast—just store data • Prediction can be slow—lots of distances to measure • Decision boundary is flexible
  • 5.
    Overview of ClassifierCharacteristics X Y • For K-Nearest Neighbors, training data is the model • Fitting is fast—just store data • Prediction can be slow—lots of distances to measure • Decision boundary is flexible
  • 6.
    Overview of ClassifierCharacteristics X Y • For K-Nearest Neighbors, training data is the model • Fitting is fast—just store data • Prediction can be slow—lots of distances to measure • Decision boundary is flexible
  • 7.
    X 0.0 1.0 Probability 0.5 𝑦 𝛽 𝑥= 1 1+𝑒−(𝛽0+ 𝛽1 𝑥 + ε ) Overview of Classifier Characteristics • For logistic regression, model is just parameters • Fitting can be slow—must find best parameters • Prediction is fast—calculate expected value • Decision boundary is simple, less flexible
  • 8.
    X 0.0 1.0 Probability 0.5 𝑦 𝛽 𝑥= 1 1+𝑒−(𝛽0+ 𝛽1 𝑥 + ε ) Overview of Classifier Characteristics • For logistic regression, model is just parameters • Fitting can be slow—must find best parameters • Prediction is fast—calculate expected value • Decision boundary is simple, less flexible
  • 9.
    X 0.0 1.0 Probability 0.5 𝑦 𝛽 𝑥= 1 1+𝑒−(𝛽0+ 𝛽1 𝑥 + ε ) Overview of Classifier Characteristics • For logistic regression, model is just parameters • Fitting can be slow—must find best parameters • Prediction is fast—calculate expected value • Decision boundary is simple, less flexible
  • 10.
    X 0.0 1.0 Probability 0.5 𝑦 𝛽 𝑥= 1 1+𝑒−(𝛽0+ 𝛽1 𝑥 + ε ) Overview of Classifier Characteristics • For logistic regression, model is just parameters • Fitting can be slow—must find best parameters • Prediction is fast—calculate expected value • Decision boundary is simple, less flexible
  • 11.
  • 12.
    Introduction to DecisionTrees • Want to predict whether to play tennis based on temperature, humidity, wind, outlook • Segment data based on features to predict result • Trees that predict categorical results are decision trees
  • 13.
    Introduction to DecisionTrees • Want to predict whether to play tennis based on temperature, humidity, wind, outlook • Segment data based on features to predict result • Trees that predict categorical results are decision trees Temperature: >= Mild Play TennisNo Tennis
  • 14.
    Play Tennis Nodes Introduction toDecision Trees • Want to predict whether to play tennis based on temperature, humidity, wind, outlook • Segment data based on features to predict result • Trees that predict categorical results are decision trees Leaves Temperature: >= Mild No Tennis
  • 15.
    Play TennisNo Tennis Nodes Leaves NoTennis Humidity: = Normal Introduction to Decision Trees • Want to predict whether to play tennis based on temperature, humidity, wind, outlook • Segment data based on features to predict result • Trees that predict categorical results are decision trees Temperature: >= Mild
  • 16.
    Play TennisNo Tennis Nodes Leaves •Want to predict whether to play tennis based on temperature, humidity, wind, outlook • Segment data based on features to predict result • Trees that predict categorical results are decision trees No Tennis Introduction to Decision Trees Temperature: >= Mild Humidity: = Normal
  • 17.
    • Example: useslope an elevation in Himalayas • Predict average precipitation (continuous value) Regression Trees Predict Continuous Values
  • 18.
    48.50 in.13.67 in. Nodes Leaves Elevation: <7900 ft. 55.42 in. Slope: < 2.5º Regression Trees Predict Continuous Values • Example: use slope an elevation in Himalayas • Predict average precipitation (continuous value)
  • 19.
    48.50 in.13.67 in. Nodes Leaves Elevation: <7900 ft. • Example: use slope an elevation in Himalayas • Predict average precipitation (continuous value) • Values at leaves are averages of members 55.42 in. Slope: < 2.5º Regression Trees Predict Continuous Values
  • 20.
    Regression Trees PredictContinuous Values 0 1 2 3 4 5 -1.0 -2.0 0.0 1.0 2.0 Source: http://scikit-learn.org/stable/auto_examples/tree/plot_tree_regression.html
  • 21.
    Regression Trees PredictContinuous Values max_depth=2 0 1 2 3 4 5 -1.0 -2.0 0.0 1.0 2.0 Source: http://scikit-learn.org/stable/auto_examples/tree/plot_tree_regression.html
  • 22.
    Regression Trees PredictContinuous Values max_depth=2 max_depth=5 0 1 2 3 4 5 -1.0 -2.0 0.0 1.0 2.0 Source: http://scikit-learn.org/stable/auto_examples/tree/plot_tree_regression.html
  • 23.
    Building a DecisionTree • Select a feature and split data into binary tree • Continue splitting with available features
  • 24.
    Building a DecisionTree • Select a feature and split data into binary tree • Continue splitting with available features
  • 25.
    Building a DecisionTree • Select a feature and split data into binary tree • Continue splitting with available features
  • 26.
    How Long toKeep Splitting? Until: • Leaf node(s) are pure (only one class remains) • A maximum depth is reached • A performance metric is achieved
  • 27.
    How Long toKeep Splitting? Until: • Leaf node(s) are pure (only one class remains) • A maximum depth is reached • A performance metric is achieved
  • 28.
    How Long toKeep Splitting? Until: • Leaf node(s) are pure (only one class remains) • A maximum depth is reached • A performance metric is achieved
  • 29.
    How Long toKeep Splitting? Until: • Leaf node(s) are pure—only one class remains • A maximum depth is reached • A performance metric is achieved
  • 30.
    • Use greedysearch: find the best split at each step • What defines the best split? • One that maximizes the information gained from the split • How is information gain defined? Building the Best Decision Tree Play Tennis Leaves No Tennis Temperature: >= Mild
  • 31.
    • Use greedysearch: find the best split at each step • What defines the best split? • One that maximizes the information gained from the split • How is information gain defined? Building the Best Decision Tree Play Tennis Leaves No Tennis Temperature: >= Mild
  • 32.
    • Use greedysearch: find the best split at each step • What defines the best split? • One that maximizes the information gained from the split • How is information gain defined? Building the Best Decision Tree Play Tennis Leaves No Tennis Temperature: >= Mild
  • 33.
    • Use greedysearch: find the best split at each step • What defines the best split? • One that maximizes the information gained from the split • How is information gain defined? Building the Best Decision Tree Play Tennis Leaves No Tennis Temperature: >= Mild
  • 34.
    Splitting Based onClassification Error 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ] Classification Error Equation Classification Error Before 1 − 8 12 = 0.3333
  • 35.
    Splitting Based onClassification Error 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ] Classification Error Equation Classification Error Before 1 − 8 12 = 0.3333
  • 36.
    Splitting Based onClassification Error 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ] Classification Error Equation Classification Error Left Side 1 − 2 4 = 0.5000 0.3333
  • 37.
    Splitting Based onClassification Error 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ] Classification Error Equation Classification Error Left Side 1 − 2 4 = 0.5000 0.3333 Information lost on small # of data points
  • 38.
    Splitting Based onClassification Error 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ] Classification Error Equation Classification Error Right Side 1 − 6 8 = 0.2500 0.3333 0.5000
  • 39.
    Splitting Based onClassification Error 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ] Classification Error Equation Classification Error Change 0.3333 − 4 12 ∗ 0.5000 − 8 12 ∗0.2500 = 0 0.3333 0.5000 0.2500
  • 40.
    Splitting Based onClassification Error 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ] Classification Error Equation Classification Error Change 0.3333 0.5000 0.2500 0.3333 − 4 12 ∗ 0.5000 − 8 12 ∗0.2500 = 0
  • 41.
    Splitting Based onClassification Error 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No • Using classification error, no further splits would occur • Problem: end nodes are not homogeneous • Try a different metric?
  • 42.
    Splitting Based onEntropy 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐻 𝑡 = − 𝑖=1 𝑛 𝑝 𝑖 𝑡 𝑙𝑜𝑔2[𝑝(𝑖|𝑡)] Entropy Equation Entropy Before − 8 12 𝑙𝑜𝑔2(8 12) − 4 12 𝑙𝑜𝑔2(4 12) = 0.9183
  • 43.
    Splitting Based onEntropy 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐻 𝑡 = − 𝑖=1 𝑛 𝑝 𝑖 𝑡 𝑙𝑜𝑔2[𝑝(𝑖|𝑡)] Entropy Equation Entropy Before − 8 12 𝑙𝑜𝑔2(8 12) − 4 12 𝑙𝑜𝑔2(4 12) = 0.9183
  • 44.
    Splitting Based onEntropy 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐻 𝑡 = − 𝑖=1 𝑛 𝑝 𝑖 𝑡 𝑙𝑜𝑔2[𝑝(𝑖|𝑡)] Entropy Equation Entropy Left Side − 2 4 𝑙𝑜𝑔2(2 4) − 2 4 𝑙𝑜𝑔2(2 4) = 1.0000 0.9183
  • 45.
    Splitting Based onEntropy 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐻 𝑡 = − 𝑖=1 𝑛 𝑝 𝑖 𝑡 𝑙𝑜𝑔2[𝑝(𝑖|𝑡)] Entropy Equation Entropy Right Side − 6 8 𝑙𝑜𝑔2(6 8) − 2 8 𝑙𝑜𝑔2(2 8) = 0.8113 0.9183 1.0000
  • 46.
    Splitting Based onEntropy 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No 𝐻 𝑡 = − 𝑖=1 𝑛 𝑝 𝑖 𝑡 𝑙𝑜𝑔2[𝑝(𝑖|𝑡)] Entropy Equation Entropy Change 0.9183 − 4 12 ∗ 1.0000 − 8 12 ∗0.8113 = 0.0441 0.9183 1.0000 0.8113
  • 47.
    Splitting Based onEntropy 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No • Splitting based on entropy allows further splits to occur • Can eventually reach goal of homogeneous nodes • Why does this work with entropy but not classification error?
  • 48.
    Splitting Based onEntropy 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No • Splitting based on entropy allows further splits to occur • Can eventually reach goal of homogeneous nodes • Why does this work with entropy but not classification error?
  • 49.
    Splitting Based onEntropy 2 Yes 2 No 6 Yes 2 No Play TennisNo Tennis Temperature: >= Mild 8 Yes 4 No • Splitting based on entropy allows further splits to occur • Can eventually reach goal of homogeneous nodes • Why does this work with entropy but not classification error?
  • 50.
    • Classification erroris a flat function with maximum at center • Center represents ambiguity—50/50 split • Splitting metrics favor results that are furthest away from the center Classification Error vs Entropy 0.0 0.5 Purity 1.0 Classification Error 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ] Error
  • 51.
    • Classification erroris a flat function with maximum at center • Center represents ambiguity—50/50 split • Splitting metrics favor results that are furthest away from the center Classification Error vs Entropy 0.0 0.5 Purity 1.0 Classification Error 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ] Error
  • 52.
    0.0 0.5 Purity 1.0 Classification Error • Classificationerror is a flat function with maximum at center • Center represents ambiguity—50/50 split • Splitting metrics favor results that are furthest away from the center 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ] Classification Error vs Entropy Error
  • 53.
    Classification Error vsEntropy • Entropy has the same maximum but is curved • Curvature allows splitting to continue until nodes are pure • How does this work? 0.0 0.5 Purity 1.0 Classification ErrorCross Entropy 𝐻 𝑡 = − 𝑖=1 𝑛 𝑝 𝑖 𝑡 𝑙𝑜𝑔2[𝑝(𝑖|𝑡)] Error/Entropy
  • 54.
    Classification Error vsEntropy • Entropy has the same maximum but is curved • Curvature allows splitting to continue until nodes are pure • How does this work? 0.0 0.5 Purity 1.0 Classification ErrorCross Entropy 𝐻 𝑡 = − 𝑖=1 𝑛 𝑝 𝑖 𝑡 𝑙𝑜𝑔2[𝑝(𝑖|𝑡)] Error/Entropy
  • 55.
    0.0 0.5 Purity 1.0 Classification ErrorCross Entropy ClassificationError vs Entropy • Entropy has the same maximum but is curved • Curvature allows splitting to continue until nodes are pure • How does this work? 𝐻 𝑡 = − 𝑖=1 𝑛 𝑝 𝑖 𝑡 𝑙𝑜𝑔2[𝑝(𝑖|𝑡)] Error/Entropy
  • 56.
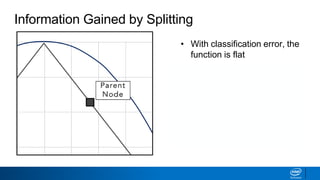
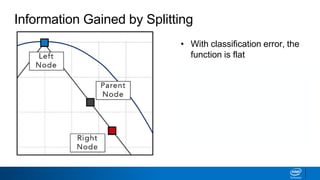
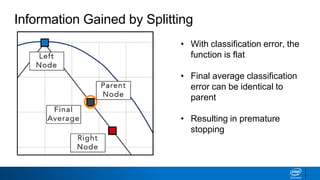
    Information Gained bySplitting • With classification error, the function is flat • Final average classification error can be identical to parent • Resulting in premature stopping
  • 57.
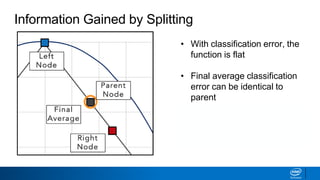
    Information Gained bySplitting • With classification error, the function is flat • Final average classification error can be identical to parent • Resulting in premature stopping
  • 58.
    Information Gained bySplitting • With classification error, the function is flat • Final average classification error can be identical to parent • Resulting in premature stopping
  • 59.
    Information Gained bySplitting • With classification error, the function is flat • Final average classification error can be identical to parent • Resulting in premature stopping
  • 60.
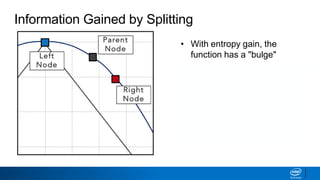
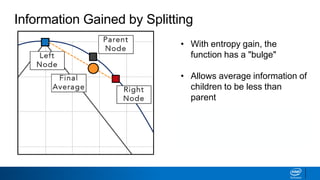
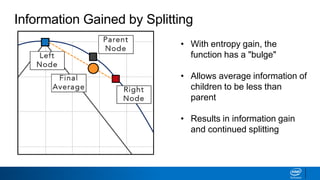
    Information Gained bySplitting • With entropy gain, the function has a "bulge" • Allows average information of children to be less than parent • Results in information gain and continued splitting
  • 61.
    Information Gained bySplitting • With entropy gain, the function has a "bulge" • Allows average information of children to be less than parent • Results in information gain and continued splitting
  • 62.
    Information Gained bySplitting • With entropy gain, the function has a "bulge" • Allows average information of children to be less than parent • Results in information gain and continued splitting
  • 63.
    0.0 0.5 Purity 1.0 Classification ErrorCross Entropy GiniIndex • In practice, Gini index often used for splitting • Function is similar to entropy—has bulge • Does not contain logarithm The Gini Index 𝐺 𝑡 = 1 − 𝑖=1 𝑛 𝑝 𝑖 𝑡 2
  • 64.
    0.0 0.5 Purity 1.0 Classification ErrorCross Entropy GiniIndex • In practice, Gini index often used for splitting • Function is similar to entropy—has bulge • Does not contain logarithm The Gini Index 𝐺 𝑡 = 1 − 𝑖=1 𝑛 𝑝 𝑖 𝑡 2
  • 65.
    0.0 0.5 Purity 1.0 Classification ErrorCross Entropy GiniIndex • In practice, Gini index often used for splitting • Function is similar to entropy—has bulge • Does not contain logarithm The Gini Index 𝐺 𝑡 = 1 − 𝑖=1 𝑛 𝑝 𝑖 𝑡 2
  • 66.
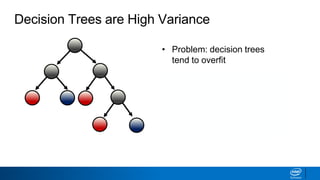
    Decision Trees areHigh Variance • Problem: decision trees tend to overfit • Small changes in data greatly affect prediction-- high variance • Solution: Prune trees
  • 67.
    • Problem: decisiontrees tend to overfit • Small changes in data greatly affect prediction-- high variance • Solution: Prune trees Decision Trees are High Variance
  • 68.
    • Problem: decisiontrees tend to overfit • Small changes in data greatly affect prediction-- high variance • Solution: Prune trees Decision Trees are High Variance
  • 69.
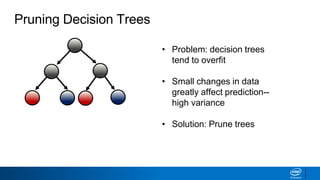
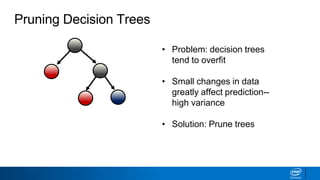
    Pruning Decision Trees •Problem: decision trees tend to overfit • Small changes in data greatly affect prediction-- high variance • Solution: Prune trees
  • 70.
    Pruning Decision Trees •Problem: decision trees tend to overfit • Small changes in data greatly affect prediction-- high variance • Solution: Prune trees
  • 71.
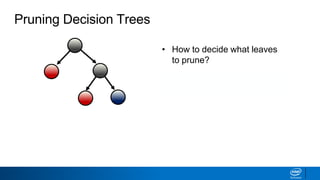
    • How todecide what leaves to prune? • Solution: prune based on classification error threshold Pruning Decision Trees
  • 72.
    • How todecide what leaves to prune? • Solution: prune based on classification error threshold Pruning Decision Trees 𝐸 𝑡 = 1 − max 𝑖 [𝑝 𝑖 𝑡 ]
  • 73.
    • Easy tointerpret and implement—"if … then … else" logic • Handle any data category— binary, ordinal, continuous • No preprocessing or scaling required Strengths of Decision Trees
  • 74.
    • Easy tointerpret and implement—"if … then … else" logic • Handle any data category— binary, ordinal, continuous • No preprocessing or scaling required Strengths of Decision Trees
  • 75.
    • Easy tointerpret and implement—"if … then … else" logic • Handle any data category— binary, ordinal, continuous • No preprocessing or scaling required Strengths of Decision Trees
  • 76.
    Import the classcontaining the classification method from sklearn.tree import DecisionTreeClassifier Create an instance of the class DTC = DecisionTreeClassifier(criterion='gini', max_features=10, max_depth=5) Fit the instance on the data and then predict the expected value DTC = DTC.fit(X_train, y_train) y_predict = DTC.predict(X_test) Tune parameters with cross-validation. Use DecisionTreeRegressor for regression. DecisionTreeClassifier: The Syntax
  • 77.
    Import the classcontaining the classification method from sklearn.tree import DecisionTreeClassifier Create an instance of the class DTC = DecisionTreeClassifier(criterion='gini', max_features=10, max_depth=5) Fit the instance on the data and then predict the expected value DTC = DTC.fit(X_train, y_train) y_predict = DTC.predict(X_test) Tune parameters with cross-validation. Use DecisionTreeRegressor for regression. DecisionTreeClassifier: The Syntax
  • 78.
    Import the classcontaining the classification method from sklearn.tree import DecisionTreeClassifier Create an instance of the class DTC = DecisionTreeClassifier(criterion='gini', max_features=10, max_depth=5) Fit the instance on the data and then predict the expected value DTC = DTC.fit(X_train, y_train) y_predict = DTC.predict(X_test) Tune parameters with cross-validation. Use DecisionTreeRegressor for regression. DecisionTreeClassifier: The Syntax tree parameters
  • 79.
    Import the classcontaining the classification method from sklearn.tree import DecisionTreeClassifier Create an instance of the class DTC = DecisionTreeClassifier(criterion='gini', max_features=10, max_depth=5) Fit the instance on the data and then predict the expected value DTC = DTC.fit(X_train, y_train) y_predict = DTC.predict(X_test) Tune parameters with cross-validation. Use DecisionTreeRegressor for regression. DecisionTreeClassifier: The Syntax
  • 80.
    DecisionTreeClassifier: The Syntax Importthe class containing the classification method from sklearn.tree import DecisionTreeClassifier Create an instance of the class DTC = DecisionTreeClassifier(criterion='gini', max_features=10, max_depth=5) Fit the instance on the data and then predict the expected value DTC = DTC.fit(X_train, y_train) y_predict = DTC.predict(X_test) Tune parameters with cross-validation. Use DecisionTreeRegressor for regression.