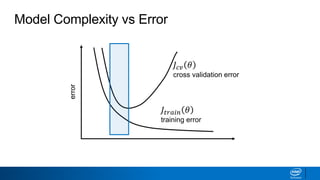
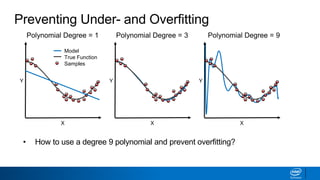
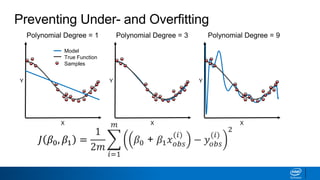
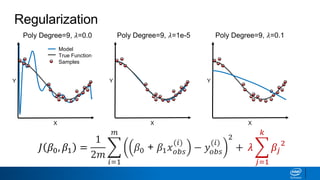
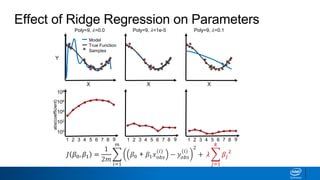
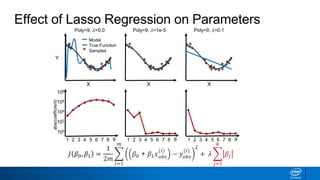
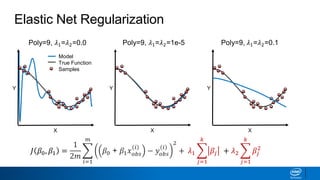
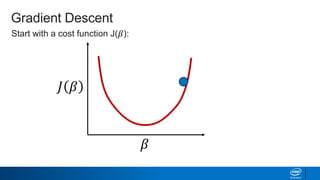
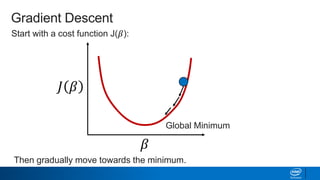
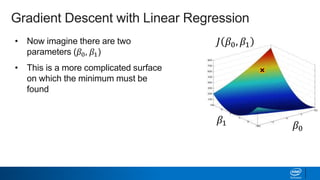
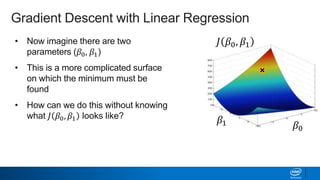
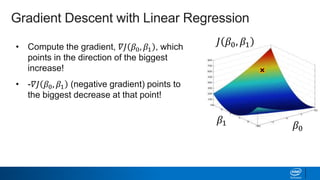
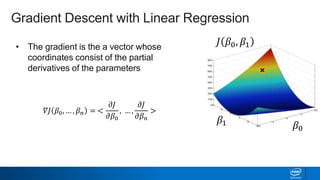
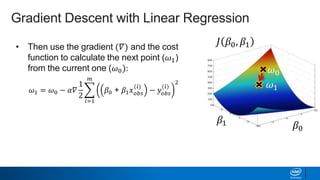
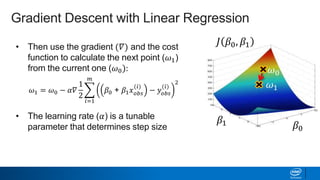
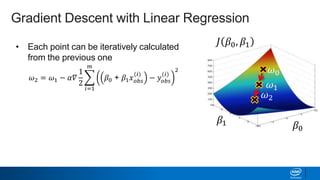
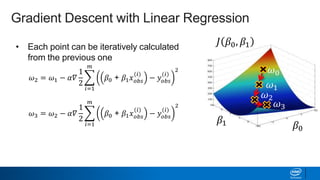
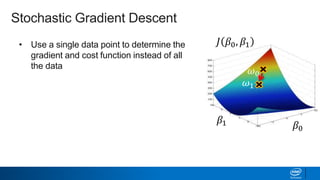
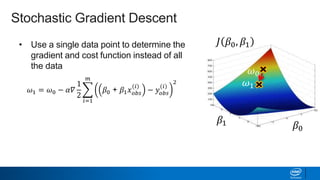
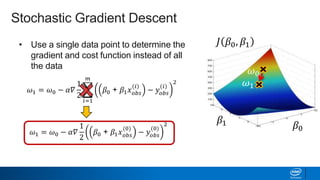
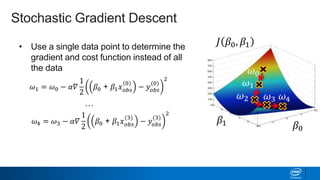
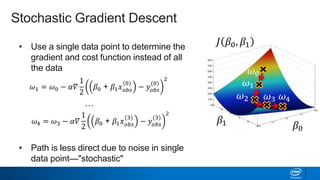
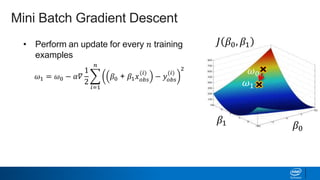
Regularization and feature selection techniques can help prevent overfitting in machine learning models. Regularization adds a penalty term to the cost function that shrinks coefficient magnitudes, while feature selection aims to identify and remove unnecessary features. Both approaches reduce model complexity to improve generalization. Ridge regression performs L2 regularization by adding a penalty term that shrinks all coefficients. Lasso regression uses L1 regularization to drive some coefficients to exactly zero, performing embedded feature selection. Elastic net is a compromise that allows for both L1 and L2 regularization. Recursive feature elimination (RFE) removes features, using a model to recursively eliminate the weakest features.