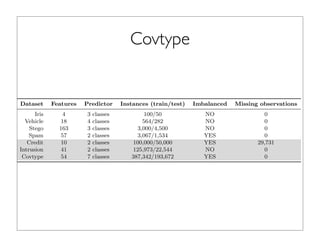
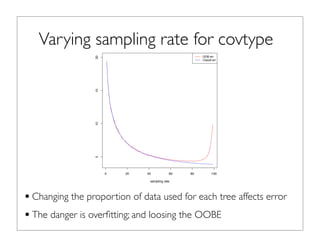
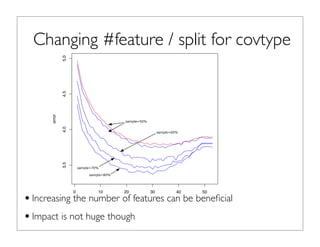
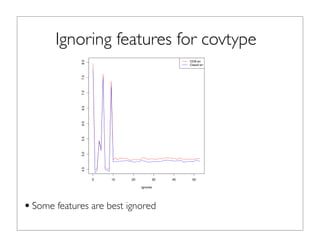
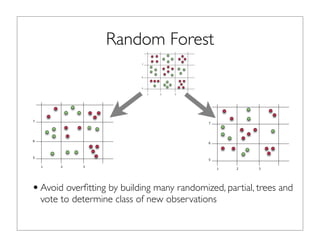
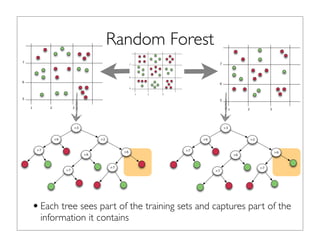
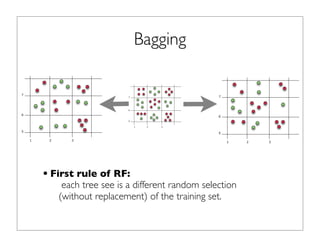
The document outlines the development and implementation of distributed random forests, detailing the advantages of using this approach for classification tasks in machine learning. It covers key concepts such as bagging, out-of-bag error estimation, and the impact of varying sampling rates and feature selection on model accuracy. The discussion includes practical examples using datasets like Iris and Covtype, as well as performance comparisons of various tools.

1. How to Grow
Distributed Random
Forests
JanVitek
Purdue University
on sabbatical at 0xdata
Photo credit: http://foundwalls.com/winter-snow-forest-pine/

2. Overview
•Not data scientist…
•I implement programming languages for a living…
•Leading the FastR project; a next generation R implementation…
•Today I’ll tell you how to grow a distributed random forest in 2KLOC

3. PART I
Why so random?
Introducing:
Random Forest
Bagging
Out of bag error estimate
Confusion matrix
Photo credit: http://foundwalls.com/winter-snow-forest-pine/
Leo Breiman. Random forests. Machine learning, 2001.

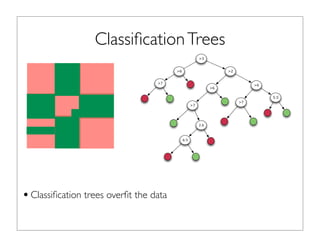
4. ClassificationTrees
•Consider a supervised learning problem with a simple data set with
two classes and the data has two features x in [1,4] and y in [5,8].
•We can build a classification tree to predict classes of new
observations
1 2 3
6
5
7

5. ClassificationTrees
•Consider a supervised learning problem with a simple data set with
two classes and the data has two features x in [1,4] and y in [5,8].
•We can build a classification tree to predict classes of new
observations
1 2 3
6
5
7
>3
>6
>7
>2
>6
>7
2.6
6.5
>6
>7
5.5

6. ClassificationTrees
•Classification trees overfit the data
>3
>6
>7
>2
>6
>7
2.6
6.5
>6
>7
5.5

7. Random Forest
•Avoid overfitting by building many randomized, partial, trees and
vote to determine class of new observations
1 2 3
6
5
7
1 2 3
6
5
7
1 2 3
6
5
7

8. Random Forest
•Each tree sees part of the training sets and captures part of the
information it contains
1 2 3
6
5
7
1 2 3
6
5
7
1 2 3
6
5
7
>3
>6
>7
>2
>6
>7
>6
>7
>3
>6
>7
>2
>6
>7
>6
>7

9. Bagging
•First rule of RF:
each tree see is a different random selection
(without replacement) of the training set.
1 2 3
6
5
7
1 2 3
6
5
7
1 2 3
6
5
7

10. Split selection
•Second rule of RF:
Splits are selected to maximize gain on a random subset
of features. Each split sees a new random subset.
>6
>7
?
Gini impurity
Information gain

11. 1 2 3
6
5
7
OOBE
•One can use the training data to get an error estimate
(“out of bag error” or OOBE)
•Validate each tree on complement of training data
1 2 3
6
5
7
1 2 3
6
5
7

12. Validation
•Validation can be done using OOBE (which is often convenient as
it does not require preprocessing) or with a separate validation
data set.
•A Confusion Matrix summarizes the class assignments performed
during validation and gives an overview of the classification errors
assigned
/ actual
Red Green
Red 15 5 33%
Green 1 10 10%

13. PART II
Demo
Running RF on Iris
Photo credit: http://foundwalls.com/winter-snow-forest-pine/

14. Iris RF results

15. Sample tree
• // Column constants
int COLSEPALLEN = 0;
int COLSEPALWID = 1;
int COLPETALLEN = 2;
int COLPETALWID = 3;
int classify(float fs[]) {
if( fs[COLPETALWID] <= 0.800000 )
return Iris-setosa;
else
if( fs[COLPETALLEN] <= 4.750000 )
if( fs[COLPETALWID] <= 1.650000 )
return Iris-versicolor;
else
return Iris-virginica;
else
if( fs[COLSEPALLEN] <= 6.050000 )
if( fs[COLPETALWID] <= 1.650000 )
return Iris-versicolor;
else
return Iris-virginica;
else
return Iris-virginica;
}

16. Comparing accuracy
•We compared several implementations and found that we are OK
all datasets most tools are reasonably accurate and give similar results. It is noteworthy that wiseRF,
ch usually runs the fastet, does not give as accurate results as R and Weka (this is the case for for the
icle, Stego and Spam datasets). H2O consistently gives the best results for these small datasets. In the
ger case studies, the tools are practically tied on Credit (with Weka and wiseRF being 0.2% better). For
usion H2O is 0.8% less accurate than wiseRF, and for the largest dataset, Covtype, H2O is markedly
re accuracte than wiseRF (over 10%).
Dataset H2O R Weka wiseRF
Iris 2.0% 2.0% 2.0% 2.0%
Vehicle 21.3% 21.3% 22.0% 22.0%
Stego 13.6% 13.9% 14.0% 14.9%
Spam 4.2% 4.2% 4.4% 5.2%
Credit 6.7% 6.7% 6.5% 6.5%
Intrusion 21.2% 19.0% 19.5% 20.4%
Covtype 3.6% 22.9% – 14.8%
. 2: The best overall classification errors for individual tools and datasets. H2O is generally the most
accurate with the exception of Intrusion where it is slightly less precise than R. R is the second
best, with the exception of larger datasets like Covtype where internal restrictions seem to result in
significant loss of accuracy.
The dataset is available at http://nsl.cs.unb.ca/NSL-KDD/. This dataset is used as benchmark of Mahout at https:
iki.apache.org/MAHOUT/partial-implementation.html
3
Dataset Features Predictor Instances (train/test) Imbalanced Missing observations
Iris 4 3 classes 100/50 NO 0
Vehicle 18 4 classes 564/282 NO 0
Stego 163 3 classes 3,000/4,500 NO 0
Spam 57 2 classes 3,067/1,534 YES 0
Credit 10 2 classes 100,000/50,000 YES 29,731
Intrusion 41 2 classes 125,973/22,544 NO 0
Covtype 54 7 classes 387,342/193,672 YES 0
Tab. 1: Overview of the seven datasets. The first four datasets are micro benchmarks that we use for
calibration. The last three datasets are medium sized problems. Credit is the only dataset with
missing observations. There are several imbalanced datasets.
2.1 Iris
The “Iris” dataset is a classical dataset http://archive.ics.uci.edu/ml/datasets/Iris. The data set
contains 3 classes of 50 instances each, where each class refers to a type of plant. One class is linearly

17. PART III
Writing a DRF algorithm
in Java with H2O
Design choices,
implementation techniques,
pitfalls.
Photo credit: http://foundwalls.com/winter-snow-forest-pine/

18. Distributing and Parallelizing RF
•When data does not fit in RAM, what impact does that have
for random forest:
•How do we sample?
•How do we select splits?
•How do we estimate OOBE?

19. Insights
•RF building parallelize extremely well when random data
sample fits in memory
•Trees can be built in parallel trivially
•Trees size increases with data volume
•Validation requires trees to be co-located with data

20. Strategy
•Start with a randomized partition of the data on nodes
•Build trees in parallel on subsets of each node’s data
•Exchange trees for validation

21. Reading and Parsing Data
•H2O does that for us and returns aValueArray which is row-
order distributed table
class ValueArray extends Iced implements Cloneable {
long numRows()
int numCols()
long length()
double datad(long rownum, int colnum) {
•Each 4MB chunk of theVA is stored on a (possibly) different
node and identified by a unique key

22. Extracting random subsets
•Each node holds a random set of 4MB chunks of the value array
final ValueArray ary = DKV.get( dataKey ).get();
ArrayList<RecursiveAction> dataInhaleJobs = new ArrayList<RecursiveAction>();
for( final Key k : keys ) {
if (!k.home()) continue; // skip non-local keys
final int rows = ary.rpc(ValueArray.getChunkIndex(k));
dataInhaleJobs.add(new RecursiveAction() {
@Override protected void compute() {
for(int j = 0; j < rows; ++j)
for( int c = 0; c < ncolumns; ++c)
localData.add ( ary.datad( j , c) );
}});
}
ForkJoinTask.invokeAll(dataInhaleJobs);

23. Evaluating splits
•Each feature that must be considered for a split requires
processing data of the form (feature value, class)
{ (3.4, red), (3.3, green), (2, red), (5, green), (6.1, green) }
•We should sort the values before processing
{ (2, red), (3.3, green), (3.4, red), (5, green), (6.1, green) }
•But since each split is done on different sets of rows, we have
to sort features at every split
•Trees can have 100k splits

24. Evaluating splits
•Instead we discretize the value
{ (2, red), (3.3, green), (3.4, red), (5, green), (6.1, green) }
•becomes
{ (0, red), (1, green), (2, red), (3, green), (4, green) }
•and no sorting is required as we can represent the colors by
arrays (of size #cardinality of the feature)
•For efficiency we can bin multiple values together

25. Evaluating splits
•The implementation of entropy based split is now simple
Split ltSplit(int col, Data d, int[] dist, Random rand) {
final int[] distL = new int[d.classes()], distR = dist.clone();
final double upperBoundReduction = upperBoundReduction(d.classes());
double maxReduction = -1; int bestSplit = -1;
for (int i = 0; i < columnDists[col].length - 1; ++i) {
for (int j = 0; j < distL.length; ++j) {
double v = columnDists[col][i][j]; distL[j] += v; distR[j] -= v;
}
int totL = 0, totR = 0;
for (int e: distL) totL += e;
for (int e: distR) totR += e;
double eL = 0, eR = 0;
for (int e: distL) eL += gain(e,totL);
for (int e: distR) eR += gain(e,totR);
double eReduction = upperBoundReduction-( (eL*totL + eR*totR) / (totL+totR) );
if (eReduction > maxReduction) { bestSplit = i; maxReduction = eReduction; }
}
return Split.split(col,bestSplit,maxReduction);

26. Parallelizing tree building
•Trees are built in parallel with the Fork/Join framework
Statistic left = getStatistic(0,data, seed + LTSSINIT);
Statistic rite = getStatistic(1,data, seed + RTSSINIT);
int c = split.column, s = split.split;
SplitNode nd = new SplitNode(c, s,…);
data.filter(nd,res,left,rite);
FJBuild fj0 = null, fj1 = null;
Split ls = left.split(res[0], depth >= maxdepth);
Split rs = rite.split(res[1], depth >= maxdepth);
if (ls.isLeafNode()) nd.l = new LeafNode(...);
else fj0 = new FJBuild(ls,res[0],depth+1, seed + LTSINIT);
if (rs.isLeafNode()) nd.r = new LeafNode(...);
else fj1 = new FJBuild(rs,res[1],depth+1, seed - RTSINIT);
if (data.rows() > ROWSFORKTRESHOLD)…
fj0.fork();
nd.r = fj1.compute();
nd.l = fj0.join();

27. Challenges
•Found out that Java Random isn’t
•Tree size does get to be a challenge
•Need more randomization
•Determinism is needed for debugging

28. PART III
Playing with DRF
Covtype,
playing with knobs
Photo credit: http://foundwalls.com/winter-snow-forest-pine/

29. Covtype
Dataset Features Predictor Instances (train/test) Imbalanced Missing observations
Iris 4 3 classes 100/50 NO 0
Vehicle 18 4 classes 564/282 NO 0
Stego 163 3 classes 3,000/4,500 NO 0
Spam 57 2 classes 3,067/1,534 YES 0
Credit 10 2 classes 100,000/50,000 YES 29,731
Intrusion 41 2 classes 125,973/22,544 NO 0
Covtype 54 7 classes 387,342/193,672 YES 0
Tab. 1: Overview of the seven datasets. The first four datasets are micro benchmarks that we use for
calibration. The last three datasets are medium sized problems. Credit is the only dataset with
missing observations. There are several imbalanced datasets.
2.1 Iris
The “Iris” dataset is a classical dataset http://archive.ics.uci.edu/ml/datasets/Iris. The data set
contains 3 classes of 50 instances each, where each class refers to a type of plant. One class is linearly
separable from the other 2; the latter are not linearly separable from each other. The dataset contains no
missing data.

30. Varying sampling rate for covtype
•Changing the proportion of data used for each tree affects error
•The danger is overfitting; and loosing the OOBE
4.2 Sampling Rate
H2O supports changing the proportion of the population that is randomly selected (without replacement)
to build each tree. Figure 1 illustrates the impact of varying the sampling rate between 1 and 99% when
building trees for Covtype.5
The blue line tracks the OOB error. It shows clearly that after approximately
80% sampling the OOBE will not improve. The red line shows the improvement in classification error, this
keeps dropping suggesting that for Covtype more data is better.
0 20 40 60 80 100
5101520
sampling rate
error
OOB err
Classif err
Fig. 1: Impact of changing the sampling rate on the overall error rate (both classification and OOB).
Recommendation: The sampling rate needs to be set to the level that minimizes the classification error.
The OOBEE is a good estimator of the classficiation error.
4.3 Feature selection

31. 0 10 20 30 40 50
4.5
ignores
2: Impact of ignoring one feature at a time on the overall error rate (both classification and OOB).
0 10 20 30 40 50
3.54.04.55.0
features
error
sample=50%
sample=60%
sample=70%
sample=80%
Impact of changing the number of features used to evaluate each split with di↵erent sampling rates
(50%, 60%, 70% and 80%) on the overall error rate (both classification and OOB).
Changing #feature / split for covtype
•Increasing the number of features can be beneficial
•Impact is not huge though

32. Ignoring features for covtype
•Some features are best ignored
0 10 20 30 40 50
4.55.05.56.06.57.07.58.0
ignores
error
OOB err
Classif err
Fig. 2: Impact of ignoring one feature at a time on the overall error rate (both classification and OOB).
5.0

33. Conclusion
•Random forest is a powerful machine learning technique
•It’s easy to write a distributed and parallel implementation
•Different implementations choices are possible
•Scaling it up toTB data comes next…
Photo credit www.twitsnaps.com