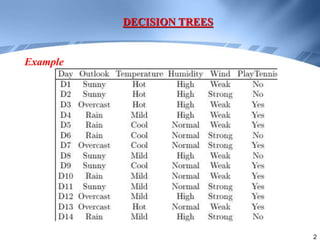
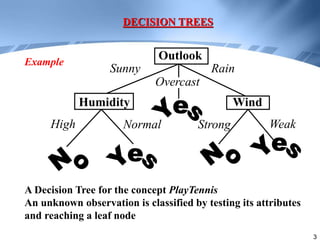
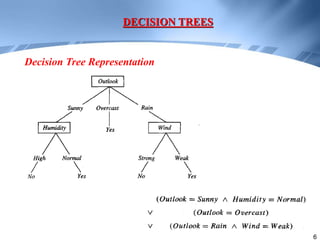
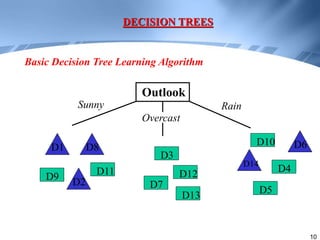
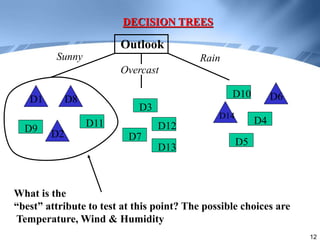
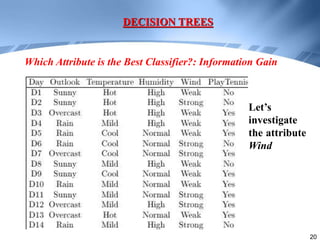
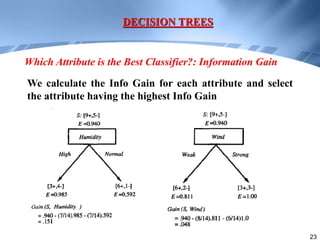
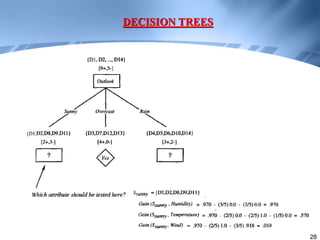
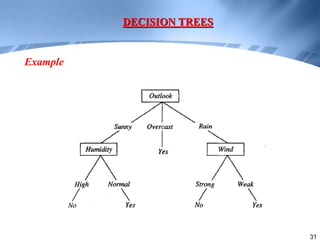
Decision trees are a supervised learning method that represents concepts as decision trees to classify data. The algorithm works by selecting the best attribute to test at each node using information gain, which measures the reduction in entropy from partitioning data by an attribute. It builds the tree in a top-down greedy manner, recursively selecting the attribute that best splits the data until the leaf nodes are pure or no further information gain is possible. The tree can then be converted to classification rules by tracing paths from the root to leaf nodes.

1. 1
It is a method that induces concepts from examples
(inductive learning)
Most widely used & practical learning method
The learning is supervised: i.e. the classes or categories of the
data instances are known
It represents concepts as decision trees (which can be
rewritten as if-then rules)
The target function can be Boolean or discrete valued
DECISION TREES
Introduction

2. 2
DECISION TREES
Example

3. 3
Outlook
Humidity Wind
Sunny
Overcast
Rain
High Normal Strong Weak
A Decision Tree for the concept PlayTennis
An unknown observation is classified by testing its attributes
and reaching a leaf node
DECISION TREES
Example

4. 4
1. Each node corresponds to an attribute
2. Each branch corresponds to an attribute value
3. Each leaf node assigns a classification
DECISION TREES
Decision Tree Representation

5. 5
Decision trees represent a disjunction of conjunctions of
constraints on the attribute values of instances
Each path from the tree root to a leaf corresponds to a
conjunction of attribute tests (one rule for classification)
The tree itself corresponds to a disjunction of these
conjunctions (set of rules for classification)
DECISION TREES
Decision Tree Representation

6. 6
DECISION TREES
Decision Tree Representation

7. 7
Most algorithms for growing decision trees are variants of a
basic algorithm
An example of this core algorithm is the ID3 algorithm
developed by Quinlan (1986)
It employs a top-down, greedy search through the space of
possible decision trees
DECISION TREES
Basic Decision Tree Learning Algorithm

8. 8
First of all we select the best attribute to be tested at the root
of the tree
For making this selection each attribute is evaluated using a
statistical test to determine how well it alone classifies the
training examples
DECISION TREES
Basic Decision Tree Learning Algorithm

9. 9
D13
D12 D11
D10
D9
D4
D7
D5
D3
D14
D8
D6
D2
D1
DECISION TREES
Basic Decision Tree Learning Algorithm
We have
- 14 observations
- 4 attributes
• Outlook
• Temperature
• Humidity
• Wind
- 2 classes (Yes, No)

10. 10
D13
D12
D11
D10
D9
D4
D7
D5
D3
D14
D8 D6
D2
D1
Outlook
Sunny
Overcast
Rain
DECISION TREES
Basic Decision Tree Learning Algorithm

11. 11
The selection process is then repeated using the training
examples associated with each descendant node to select the
best attribute to test at that point in the tree
DECISION TREES
Basic Decision Tree Learning Algorithm

12. 12
D13
D12
D11
D10
D9
D4
D7
D5
D3
D14
D8 D6
D2
D1
Outlook
Sunny
Overcast
Rain
What is the
“best” attribute to test at this point? The possible choices are
Temperature, Wind & Humidity
DECISION TREES

13. 13
This forms a greedy search for an acceptable decision tree, in
which the algorithm never backtracks to reconsider earlier
choices
DECISION TREES
Basic Decision Tree Learning Algorithm

14. 14
The central choice in the ID3 algorithm is selecting which
attribute to test at each node in the tree
We would like to select the attribute which is most useful for
classifying examples
For this we need a good quantitative measure
For this purpose a statistical property, called information
gain is used
DECISION TREES
Which Attribute is the Best Classifier?

15. 15
In order to define information gain precisely, we begin by
defining entropy
Entropy is a measure commonly used in information theory,
called.
Entropy characterizes the impurity of an arbitrary collection
of examples
DECISION TREES
Which Attribute is the Best Classifier?: Definition of Entropy

16. 16
Suppose there are 14 samples and 9 samples are positive and
5 negative then probabilities can be calculated as:
A= 9, B = 5
p(A) = 9/14
p(B) = 5/14
The entropy of X is
DECISION TREES
Which Attribute is the Best Classifier?: Definition of Entropy

17. 17
This formula is called Entropy H
H(X) =
High Entropy means that the examples have more equal
probability of occurrence (and therefore not easily
predictable)
Low Entropy means easy predictability
DECISION TREES
Which Attribute is the Best Classifier?: Definition of Entropy

18. Entropy
• Entropy is 0 if all members of S belong to the
same class.
• For example, if all members are positive (p+ = I), then
p-, is 0, and
• Entropy(S) = -1 . log2(1) - 0 . log2 0
• = -1 . 0 - 0 . log2 0
• = 0.
• Note the entropy is 1 when the collection contains an equal number of
positive and negative examples.
• If the collection contains unequal numbers of positive and negative
examples, entropy is between 0 and 1.
18

19. 19
Information Gain is the expected reduction in entropy
caused by partitioning the examples according to an
attribute’s value
Info Gain (Y | X) = H(Y) – H(Y | X) = 1.0 – 0.5 = 0.5
For transmitting Y, how much bits would be saved if both
side of the line knew X
In general, we write Gain (S, A)
Where S is the collection of examples & A is an attribute
DECISION TREES
Which Attribute is the Best Classifier?: Information Gain

20. 20
Let’s
investigate
the attribute
Wind
DECISION TREES
Which Attribute is the Best Classifier?: Information Gain

21. 21
The collection of examples has 9 positive values and 5
negative ones
DECISION TREES
Which Attribute is the Best Classifier?: Information Gain
Eight (6 positive and 2 negative ones) of these examples
have the attribute value Wind = Weak
Six (3 positive and 3 negative ones) of these examples have
the attribute value Wind = Strong

22. 22
The information gain obtained by separating the
examples according to the attribute Wind is calculated as:
DECISION TREES
Which Attribute is the Best Classifier?: Information Gain

23. 23
We calculate the Info Gain for each attribute and select
the attribute having the highest Info Gain
DECISION TREES
Which Attribute is the Best Classifier?: Information Gain

24. 24
Make decision tree by selecting tests which minimize
disorder (maximize gain)
DECISION TREES
Select Attributes which Minimize Disorder

25. 25
Make decision tree by selecting tests which minimize
disorder (maximize gain)
DECISION TREES
Select Attributes which Minimize Disorder

26. 26
DECISION TREES
Select Attributes which Minimize Disorder
The formula can be converted from log2 to log10
logx(M) = log10M . logx10
= log10M/log10x
Hence log2(Y) = log10(Y)/log10(2)

27. 27
DECISION TREES
Example
Which attribute should be selected as the first test?
“Outlook” provides the most information

28. 28
DECISION TREES

29. 29
DECISION TREES
Example
The process of selecting a new attribute is now repeated for
each (non-terminal) descendant node, this time using only
training examples associated with that node
Attributes that have been incorporated higher in the tree are
excluded, so that any given attribute can appear at most once
along any path through the tree

30. 30
DECISION TREES
Example
This process continues for each new leaf node until either:
1. Every attribute has already been included along this path
through the tree
2. The training examples associated with a leaf node have
zero entropy

31. 31
DECISION TREES
Example

32. 32
Next Step: Make rules from the decision tree
After making the identification tree, we trace each path from
the root node to leaf node, recording the test outcomes as
antecedents and the leaf node classification as the consequent
For our example we have:
If the Outlook is Sunny and the Humidity is High then No
If the Outlook is Sunny and the Humidity is Normal then Yes
...
DECISION TREES
From Decision Trees to Rules

33. 33
ID3 can be characterized as
searching a space of
hypotheses for one that fits
the training examples
The space searched is the set
of possible decision trees
ID3 performs a simple-to-
complex, hill-climbing
search through this
hypothesis space
DECISION TREES
Hypothesis Space Search

34. 34
It begins with an empty tree,
then considers more and
more elaborate hypothesis
in search of a decision tree
that correctly classifies the
training data
The evaluation function that
guides this hill-climbing
search is the information
gain measure
DECISION TREES
Hypothesis Space Search

35. 35
Some points to note:
• The hypothesis space of all decision trees is a complete
space. Hence the target function is guaranteed to be
present in it.
DECISION TREES
Hypothesis Space Search

36. 36
• ID3 maintains only a single current hypothesis as it
searches through the space of decision trees.
By determining only a single hypothesis, ID3 loses the
capabilities that follow from explicitly representing all
consistent hypotheses.
For example, it does not have the ability to determine
how many alternative decision trees are consistent with
the training data, or to pose new instance queries that
optimally resolve among these competing hypotheses
DECISION TREES
Hypothesis Space Search

37. 37
• ID3 performs no backtracking, therefore it is
susceptible to converging to locally optimal solutions
• ID3 uses all training examples at each step to refine its
current hypothesis. This makes it less sensitive to
errors in individual training examples.
However, this requires that all the training examples
are present right from the beginning and the learning
cannot be done incrementally with time
DECISION TREES
Hypothesis Space Search