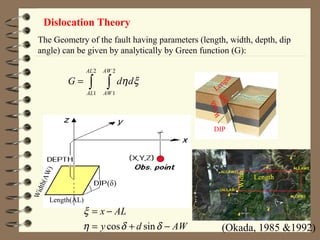
1. The document discusses different methods of modeling fault geometry and slip, including analytical Green's function methods, dislocation theory, and forward and inverse modeling approaches. 2. It also describes the Coulomb software which models fault slip using inputs of fault length, width, dip angle, strike slip, and dip slip. 3. Finite element and boundary element methods are presented for relating observed displacement data to fault source parameters through systems of equations involving the fault geometry Green's function.

1. Method of Modelling
Kutubuddin ANSARI
kutubuddin.ansari@ikc.edu.tr
GNSS Surveying, GE 205
Lecture 12, May 22, 2015

2. The Geometry of the fault having parameters (length, width, depth, dip
angle) can be given by analytically by Green function (G):
2 2
1 1
AL AW
AL AW
G d dη ξ= ∫ ∫
(Okada, 1985 &1992)
Length
Width
DIP
Slip
Length(AL)
Width(AW)
Length
Width
cos sin
x AL
y d AW
ξ
η δ δ
= −
= + −
(δ)
Dislocation Theory

3. (P. Cervelli et. al 2001)
S is Slip For Oblique Slip
S= s.cosα + s.sinα
d= sG(m)
Relationship between dislocation field (d) and the fault
geometry G(m)

4. Since the ruptured area is not a perfect finite rectangular
and it contains error the Cervelli equation becomes
Forward Modelling Approach
d= sG(m)+
d-sG(m)
0
ˆ ˆ ˆd= sG(m)
if
ε
ε
ε
=
→
where
m=initial model parameter
ˆ mod
ˆ mod
ˆ mod
s slip
error
S Net slip
d elled dislocaton field
s el slip
m el parameter
rake of the netslip on the fault plane
ε
α
=
=
=
=
=
=
=For Oblique Slip
S= s.cosα + s.sinα

5. Coulomb Software
Coulomb software is based on the Boundary
Element Method (BEM). The inputs given to
Coulomb are estimates of length, width, dip
angle, strike slip and dip slip of the modelled
fault plane as well as the co-ordinates of the
trace of the fault plane.
(Toda et al., 2010)

6. Coulomb Input File (Toda et al., 2010)

7. Coulomb Input File (Toda et al., 2010)

8. The relation between displacement field and the source geometry can be
expressed by the following equation:
( )
( )
d G m
d sG m
α
=
Where d= displacement vector
m=source geometry (dislocation, length, width, depth, strike, dip)
s=slip
(P. Cervelli et al., 2001)
Inverse Modelling

9. If we have observed data d1
, d2
, …dn
and the Green function of each
observation data are G1
, G2
, …Gn
respectively, Then-
1 11 12 1 1
2 21 22 2 2
1 2
.........
.........
. . .
. . .
. . .
.........
m
m
n n n nm m
d G G G m
d G G G m
d G G G m
    
    
    
    
=    
    
    
    
        
1
1 11 12 1 1
2 21 22 2 2
1 2
.........
.........
. . .
. . .
. . .
.........
m
m
m n n nm n
m G G G d
m G G G d
m G G G d
−
     
     
     
     
=     
     
     
     
          
Least square approach

10. Cartesian Co-ordinate system (x,y,z) the half space occupied
region z<0 if fault is located at (0,0,-d) the point force
distribution can be given in following form .
Finite Element Method
μ, λ are lames constants

11. Thrust faults :-
F1 and F2 will be horizontal and F3 will be vertical.
Normal faults:-
F2 and F3 will be horizontal and F1 will be vertical
Strike-slip faults:-
F1 and F3 will be horizontal and F2 will be vertical

13. ANSYS (Brick 8 node 185) element, White concentrated area is
showing finite rectangular fault

14. Where Fi is acting force and ui and vi displacements of
points and ki
j are Stifness constants

15. At location of fault points