My presentation slides (3)

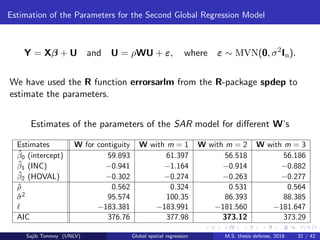
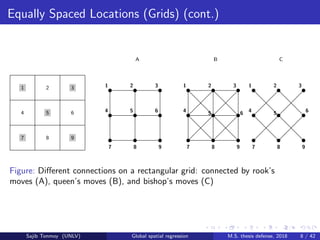
Estimation of the parameters
in a spatial regressive-autoregressive model
using Ord’s eigenvalue method
Sajib Tonmoy
Department of Mathematical Sciences
University of Nevada, Las Vegas
M.S. thesis defense, 2018
Sajib Tonmoy (UNLV) Global spatial regression M.S. thesis defense, 2018 1 / 42

Outline
Ord (1975) considered spatial regressive-autoregressive models to describe
the interaction between location and a response variable in the presence of
several covariates (predictors).
He also developed a practical estimation method of the parameters of this
regression model.
In this thesis, we reviewed his estimation method and implemented it in
the statistical package R.

The Models of Whittle, Bartlett, and Besag
For i = 1, . . . , n, suppose Yi is a response variable at location i. To describe the spatial
interaction between locations for the response variable, Whittle (1954) considered the
following autoregressive model:
Yi = α + ρ
j∈J(i)
wij Yj + εi (i = 1, . . . , n). (1)
Here,
ρ and α are parameters;
the εi ’s (i = 1, . . . , n) are random disturbance terms which are uncorrelated, have
equal variances, and zero means;
the wij ’s are non-negative weights (with wii = 0) that represent the “degree of
interactions” of each location i with the set of neighboring locations
J(i) = {i1, i2, . . . , imi }.
Remark
Here, J(i) may include all locations except location i. Note that,
n
i=1
J(i) ⊆ {1, 2, . . . , n}.

The Models of Whittle, Bartlett, and Besag (cont.)
Bartlett (1966, 1971) and Besag (1972) considered the following conditional model:
E[Yi | Yj = yj , j ∈ J(i) ] = α + ρ
k∈J(i)
wik yk (i = 1, . . . , n). (2)
The following lemma shows the relationship between models (1) and (2):
Lemma
(a) If equations (1) and (2) hold, then
E[εi | Yj = yj , j ∈ J(i)] = 0 (i = 1, . . . , n). (3)
(b) If equations (1) and (3) hold, then equation (2) holds as well.

Ord’s Global Regression Models
The ﬁrst global spatial regression model Ord (1975) considered is
Y = Xβ + ρWY + ε, where ε ∼ MVN(0, σ2In).
Here,
X is an n × p design matrix;
β is a p × 1 vector of (unknown) coeﬃcients;
W is an n × n weight matrix, whose (i, j)-th element is wij ;
Y = (y1, . . . , yn) is an n × 1 vector of response variables;
ε = (ε1, . . . , εn) is an n × 1 vector of random disturbance terms; and
ρ is an unknown parameter.

Ord’s Global Regression Models (cont.)
The second global spatial regression model Ord (1975) considered is
Y = Xβ + U and U = ρWU + ε, where ε ∼ MVN(0, σ2In).
Here,
X is an n × p design matrix;
β is a p × 1 vector of (unknown) coeﬃcients;
W is an n × n weight matrix, whose (i, j)-th element is wij ;
Y = (y1, . . . , yn) is an n × 1 vector of response variables;
ε = (ε1, . . . , εn) is an n × 1 vector of random disturbance terms;
U = (u1, . . . , un) is an n × 1 vector of disturbance terms; and
ρ is an unknown parameter.

Equally Spaced Locations (Grids)
For equally spaced locations, we can set wij > 0 if and only if location j is
a “neighbour” to location i.
In a regular grid, generally, we consider the following forms of connections
to ﬁnd the weight matrix:
connections by rook’s moves
connections by bishop’s moves
connections by queen’s moves

Equally Spaced Locations (Grids) (cont.)
1
4
7 8
5
2
9
6
3
7 8 9
4 5 6
1 2 3
A
7 8 9
4 5 6
1 2 3
B
7 8 9
4 5 6
1 2 3
C
Figure: Diﬀerent connections on a rectangular grid: connected by rook’s
moves (A), queen’s moves (B), and bishop’s moves (C)

Equally Spaced Locations (Grids) (cont.)
For the ﬁgure on the previous slide, the following weight matrix
corresponds to the connections by queen’s moves for each of the 9
locations:
Wqueen =
1 2 3 4 5 6 7 8 9
























1 0 1 0 1 1 0 0 0 0
2 1 0 1 1 1 1 0 0 0
3 0 1 0 0 1 1 0 0 0
4 1 1 0 0 1 0 1 1 0
5 1 1 1 1 0 1 1 1 1
6 0 1 1 0 1 0 0 1 1
7 0 0 0 1 1 0 0 1 0
8 0 0 0 1 1 1 1 0 1
9 0 0 0 0 1 1 0 1 0

Weight Matrices for Irregular Lattices
In real world data, most of the time we have to deal with irregular lattice
structures of many locations.
Following Pace and Barry (1997), in the case of an irregular lattice, we
can use the distances among locations to ﬁnd the mth nearest neighbors
of location i, in order to create a weight matrix W.

Weight Matrices for Irregular Lattices (cont.)
Here, we explain how to create a weight matrix Wm based on mth nearest
neighbors.
For each m ≥ 1 and 1 ≤ i, j ≤ n, we deﬁne the (i, j)-th element of matrix
Wm by
w
(m)
ij =
1, if dij ≤ d
(m)
(max,i) and i = j,
0, otherwise.
Here,
d
(m)
(max,i) := mth order statistic of the distances
di,1, di,2, . . . , di,i−1, di,i+1, . . . , di,n.
(Recall that di,i = 0.)

1
2
3
4
5
d45
d42
d23
d31
d15
d53
d52 d21
d41
d43
Figure: An example of an irregular lattice with ﬁve locations

The relative values of the Euclidean distances dij among the ﬁve points in
the previous ﬁgure are as follows:
d21 = 5.83, d23 = 2.83, d42 = 3.61, d52 = 7.00, d31 = 3.16,
d43 = 4.12, d53 = 5.39, d41 = 5.39, d15 = 3.61, d45 = 4.47.
For each m ∈ {1, 2, 3, 4}, we may create a weight matrix, Wm, using the
mth nearest neighbour to each location i.

For m = 2, the distances from each location i to the second nearest
neighbour are as follows:
d
(2)
(max,1) = 3.61, d
(2)
(max,2) = 3.61, d
(2)
(max,3) = 3.16,
d
(2)
(max,4) = 4.12, d
(2)
(max,5) = 4.47.
Then the corresponding weight matrix is as follows:
W2 =
1 2 3 4 5










1 0 0 1 0 1
2 0 0 1 1 0
3 1 1 0 0 0
4 0 1 1 0 0
5 1 0 0 1 0
In a similar way, we can create the weight matrices W1, W3, and W4.

Eigenvalues of a Row-standardized Weight Matrix
Lemma
Let W be a row-standardized matrix with non-negative elements. Then W
has (possibly complex) eigenvalues λ1, . . . , λn such that
|λi | ≤ 1, for i = 1, . . . , n,
and one of the eigenvalues is equal to 1.

Equations for the MLEs of the Parameters in a Global Spatial Regression Model
Theorem
Assume ε ∼ MVN(0, σ2I) and Y = Xβ + ρWY + ε. Then the MLEs of
the parameters β, σ2, and ρ satisfy the following equations:
ˆβ = (X X)−1
X (I − ˆρW)y,
ˆσ2 =
1
n
y (I − ˆρW) (I − H)(I − ˆρW)y,
and − ˆσ2
Tr[(I − ˆρW)−1
W] + y Wy − ˆρ y W Wy − ˆβ X Wy = 0.
Here, I − H is symmetric and idempotent, where H = X(X X)−1X is
the usual hat matrix in linear regression.

Properties of the Determinant of the Matrix I − ρW
Lemma
If W has (possibly complex) eigenvalues λ1, λ2, . . . , λn, then
det(I − ρW) =
n
i=1
(1 − ρλi ),
and
∂ ln det(I − ρW)
∂ρ
= Tr[(I − ρW)−1
W] = −
n
i=1
λi
1 − ρλi
.
The ﬁrst equality of the second equation follows from Jacobi’s formula
for the derivative of the determinant of a square matrix.

Equation for the MLE of ρ
Theorem
Assume ε ∼ MVN(0, σ2
I) and Y = Xβ + ρWY + ε. The MLE of the parameter
ρ satisﬁes the following equation:
−
ˆρ2
n
[h1
n
i=1
λi
1 − ˆρλi
] + ˆρ [−h1 +
2h2
n
n
i=1
λi
1 − ˆρλi
] + [h2 −
h3
n
n
i=1
λi
1 − ˆρλi
] = 0,
where λ1, . . . , λn are the eigenvalues of W and
h1 = y [W (I − H)W]y;
h2 = y [W (I − H)]y;
h3 = y (I − H)y.
To ﬁnd a solution for ˆρ from the above equation, we used the R function
uniroot.

Log-likelihood Equation
Remark
For the mixed regressive-autoregressive model, the log-likelihood equation has the
following form:
(β, σ2
, ρ; y) = ln (det(I − ρW)) −
n
2
ln(2πσ2
)
−
1
2σ2
[y (I − ρW) (I − ρW)y − 2β X (I − ρW)y + β X Xβ].

The Columbus, Ohio, Crime Data from 1980
We implement Ord’s eigenvalue method in a global spatial regression
that involves the Columbus, Ohio, crime data from 1980.
The data set concerns 49 contiguous neighborhoods in Columbus, Ohio.
The neighborhood list corresponds to a list of census tracks.

Natural Contiguity of Neighborhoods in Columbus, Ohio
Figure: Neighborhoods in Columbus, Ohio
The above ﬁgure originally appeared on p. 188 of the book Spatial Econometrics:
Methods and Models, by Luc Anselin.

Description of the Variables in the Columbus, Ohio, Data
From the data set, we used three variables: CRIME, HOUSE, and INC.
In the dataset, we also used the X and Y variables that represent the
relative coordinates (with respect to some origin) of the geographical
center of each neighborhood.
We used these coordinates to construct diﬀerent weight matrices for our
spatial regression model.

Weight Matrix Using Natural Contiguity of Neighbors
We wrote our own R code to implement Ord’s eigenvalue method to
estimate the parameters of the model
Y = Xβ + ρWY + ε with ε ∼ MVN(0, σ2
I).
For this data set, X is a 49 × 3 design matrix with all ones in its ﬁrst
column, β is a 3 × 1 vector of coeﬃcients, W is a 49 × 49 weight matrix,
and Y and ε are 49 × 1 matrices.
First we used a weight matrix W that can be obtained using the natural
contiguity of the neighborhoods.

Weight Matrix Using mth
Nearest Neighbors
To create a weight matrix using the mth nearest neighbors, ﬁrst we used
the coordinates of the neighborhoods (the X and Y variables in the data
set) to calculate the distances from each location i to the neighborhood
locations.
For example, the distances for the third nearest neighbour (i.e., m = 3) are
as follows:
d
(3)
(max,1) = 3.828, d
(3)
(max,2) = 3.385, d
(3)
(max,3) = 2.624, . . . , d
(3)
(max,49) = 3.444.

Row-standardizing the Weight Matrix
The mth nearest neighbor condition on the (i, j)-th element of matrix Wm,
yields a weight of 1 for the census blocks j that are within the mth nearest
neighbour of location i, and 0 otherwise.
We used the following formula to create a row-standardized weight matrix:
Wm = ˜w
(m)
ij
n
i,j=1
, where ˜w
(m)
ij =
w
(m)
ij
n
=1 w
(m)
i
for 1 ≤ i, j ≤ n.
We wrote a R code which produces weight matrices based on mth nearest
neighbours.

Estimation of the Parameters for the First Global Regression Model
Y = Xβ + ρWY + ε, where ε ∼ MVN(0, σ2
In).
We used our own R code to estimate the parameters. To check our
results, we also used the R function lagsarlm from the R-package spdep.
Estimates of the parameters of the 1st model for diﬀerent W’s
Estimates W for contiguity W with m = 1 W with m = 2 W with m = 3
ˆβ0 (intercept) 45.080 50.539 41.192 42.040
ˆβ1 (INC) −1.032 −1.158 −0.924 −0.941
ˆβ2 (HOVAL) −0.266 −0.282 −0.260 −0.266
ˆρ 0.431 0.306 0.453 0.443
ˆσ2 95.495 93.644 81.885 86.261
−182.390 −182.124 −179.407 −180.065
AIC 374.780 374.248 368.814 370.130

Estimation of the Parameters for the First Global Regression Model (cont.)
Standard errors of the parameters of the 1st model for diﬀerent W’s
Standard Error W for contiguity W with m = 1 W with m = 2 W with m = 3
ASE(ˆβ0) 7.1773 5.6959 6.2953 6.6462
ASE(ˆβ1) 0.3051 0.2885 0.2803 0.2884
ASE(ˆβ2) 0.0885 0.0875 0.0820 0.0841
ASE(ˆρ) 0.1177 0.0833 0.0976 0.1058

−1.0 −0.5 0.0 0.5 1.0
−20000−15000−10000−50000500010000
rho
equationforrho
Figure: Graph of the LHS of the equation satisﬁed by ˆρ for W with natural
contiguity

−1.0 −0.5 0.0 0.5 1.0
−2e+050e+002e+054e+056e+05
rho
equationforrho
Figure: Graph of the LHS of the equation satisﬁed by ˆρ for W when m = 1

−1.0 −0.5 0.0 0.5 1.0
−40000−200000200004000060000
rho
equationforrho

−1.0 −0.5 0.0 0.5 1.0
−30000−20000−10000010000
rho
equationforrho

Estimation of the Parameters for the Second Global Regression Model
Y = Xβ + U and U = ρWU + ε, where ε ∼ MVN(0, σ2
In).
We have used the R function errorsarlm from the R-package spdep to
estimate the parameters.
Estimates of the parameters of the SAR model for diﬀerent W’s
Estimates W for contiguity W with m = 1 W with m = 2 W with m = 3
ˆβ0 (intercept) 59.893 61.397 56.518 56.186
ˆβ1 (INC) −0.941 −1.164 −0.914 −0.882
ˆβ2 (HOVAL) −0.302 −0.274 −0.263 −0.277
ˆρ 0.562 0.324 0.531 0.564
ˆσ2 95.574 100.35 86.393 88.385
−183.381 −183.991 −181.560 −181.647
AIC 376.76 377.98 373.12 373.29

Estimation of the Parameters for the Second Global Regression Model (cont.)
Standard errors of the parameters of the 2nd model for diﬀerent W’s
Standard Error W for contiguity W with m = 1 W with m = 2 W with m = 3
ASE(ˆβ0) 5.3662 4.7587 5.2873 5.4150
ASE(ˆβ1) 0.3305 0.3143 0.3199 0.3193
ASE(ˆβ2) 0.0905 0.0909 0.0848 0.0869
ASE(ˆρ) 0.1339 0.0997 0.1101 0.1199

Prediction for the First Spatial Regression Model
For the first global spatial regression model Y = Xβ + ρWY + ε, where
ε ∼ MVN(0, σ2
In), the predicted model can be found as follows:
ˆY = X ˆβ + ˆρWˆY =⇒ (I − ˆρW)ˆY = X ˆβ
=⇒ ˆY = (I − ˆρW)−1
X ˆβ.
Remark
For the predicted vector ˆY to make sense, we need to find the
variance-covariance matrix Var(ˆY).
This, however, seems quite complicated and we did not attempt it.
This computation does involve the variance-covariance matrix of ˆβ, which
(in principle) we can estimate asymptotically, but the computation seems
quite complicated.
It might involve implicitly defined equations involving higher moments and
cross-moments.

Prediction for the Second Global Regression Model
For the second global regression model, called Simultaneous
Autoregressive (SAR) error model, in the equations
Y = Xβ + U and U = ρWU + ε,
we may replace U as follows:
Y − Xβ = ρW(Y − Xβ) + ε =⇒ Y = Xβ + ρWY − ρWXβ + ε.

Prediction for the Second Global Regression Model (cont.)
In this case, the predicted model becomes:
ˆY = X ˆβ + ˆρWˆY − ˆρWX ˆβ =⇒ (I − ˆρW)ˆY = (I − ˆρW)X ˆβ
=⇒ ˆY = X ˆβ.
Remark
Here,
Var(ˆY) = XVar( ˆβ)X ,
and we should be able (in principle) to calculate Var( ˆβ) asymptotically
using the second partial derivatives of the log-likelihood. We did not
attempt that.

Bibliography
Anselin, L.,
Spatial Econometrics: Methods and Models,
Boston: Kluwer Academic Publishers, 1988.
Bartlett, M. S.,
Physical nearest neighbour models and non-linear time series,
Journal of Applied Probability, 8(2), 222–232, 1971.
Besag, J. E.,
Nearest neighbour systems and the auto-logistic model for binary
data,
Journal of the Royal Statistical Society, Ser. B, 34(1), 75–83, 1972.

Bibliography (cont.)
Besag, J. E.,
Spatial interaction and the statistical analysis of lattice systems,
Journal of the Royal Statistical Society, Ser. B, 36(2), 192–236, 1974.
Fotheringham, A. S., Brunsdon, C., and Charlton, M.,
Geographical Weighted Regression,
Hoboken, New Jersey: John Wiley & Sons, 2002.
Hijmans, R. (2016), Spatial Data Analysis and Modeling with R.
Available at http://rspatial.org/.
Matthews, K. (2017), Markov matrices, online notes in the Number
Theory Web, available at:
http://www.numbertheory.org/courses/MP274/markov.pdf,
accessed August 31, 2018.

Ord, K.,
Estimation methods for models of spatial interaction,
Journal of the American Statistical Association, 70(349), 120–126,
1975.
O’Sullivan, D. and Unwin, D. J.,
Geographic information analysis,
Hoboken, New Jersey: John Wiley & Sons, 2010.
Pace, R. K. and Barry, R.
Sparse spatial autoregression,
Statistics & Probability Letters, 33(3), 291–297, 1997.
R Package Documentation, COL.OLD: Columbus OH spatial analysis
data set - old numbering, available at
https://rdrr.io/rforge/spdep/man/COL.OLD.html.

Sokal, R. R. and Oden, N. L.,
Spatial autocorrelation in biology: 1. Methodology,
Biological Journal of the Linnean Society, 10(2), 199–228, 1978.
United States Census Bureau, Geographic Terms and Concepts -
Census Tract, available at
https://www.census.gov/geo/reference/gtc/gtc_ct.html,
accessed October 7, 2018.
Whittle, P.,
On Stationary Processes in the Plane,
Biometrika, 41(Parts 3 and 4), 434–449, 1954.

THANK YOU!

QUESTIONS!

My presentation slides (3)

More Related Content

What's hot

Similar to My presentation slides (3)

Recently uploaded

My presentation slides (3)