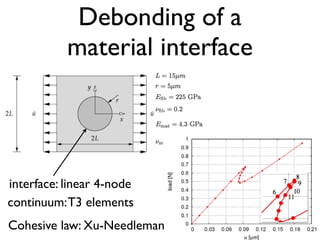
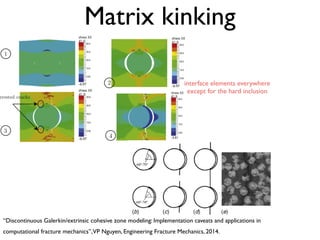
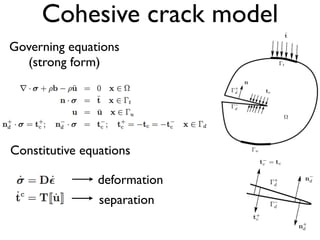
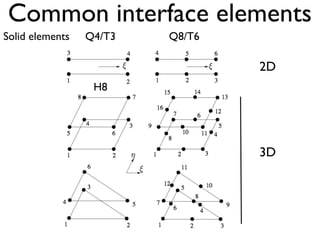
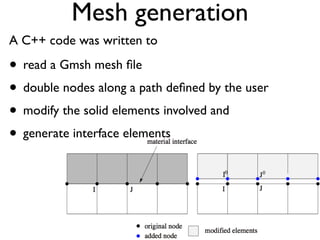
This document discusses using zero-thickness interface elements to model cracks in finite element analysis. It introduces interface elements and cohesive crack models, describes how to formulate and implement them in finite element codes, and provides some examples of their use. Key aspects covered include discrete equations for interface elements, numerical integration techniques, cohesive laws, solution procedures like load control and energy control path following methods, and examples applying interface elements to material debonding and delamination problems.

1. Crack modelling using
zero-thickness interface elements
Nguyen Vinh Phu
!
The University of Adelaide

2. Introduction
There exists problems in which the
crack path is known in advance...
inter-granular cracking in
polycrystals
delaminated
composites

3. Introduction (cont.)
...then the use of interface elements is recommended
• easy to implement (2D, 3D)
• available in major FE packages: ABAQUS, LS-DYNA
Alternatives:
XFEM/GFEM

4. Cohesive crack model
Governing equations
(strong form)
Constitutive equations
deformation
separation

5. Cohesive crack model
Weak form
new term
(skipped for static problems)
where

6. Discrete equations
upper face
lower face
Solid elements
Discrete equation
N1 = 0.5(1 ⇠)
N2 = 0.5(1 + ⇠)

7. Discrete equations (cont.)
assembled
Static problems
f ext = f int + f coh
Linearization (Newton-Raphson)
transformation matrix

9. Common interface elements
2D
3D
Solid elements Q4/T3 Q8/T6
H8

10. Numerical integration
It has been observed numerically that integrating the
internal force and stiffness matrix of interface elements
using the standard Gauss rule led to oscillatory response
[de Borst, IJNME, 1993].
Newton-Cotes integration scheme
for interface elements

11. Cohesive laws
Mode I Bilinear cohesive law (traction-separation law)
tensile strength
k
fracture energy
crack initiation
crack propagation
GIc =
1
2
tcf =
1
2
kcf
f =
2GIc
kc
c =
tc
k
t = (1 d)k
d =
8
:
!f
!
 if loading
max!f
max(!f !c) + !c
otherwise
 =
c
f c
elastic stiffness

12. Implementation aspects
• How to generate interface element meshes?
• Solution control
- load control:
- displacement control
- path following control
(arc-length methods)
F
u
cannot pass the snap-through
NO
cannot pass the snap-back

13. Mesh generation
A C++ code was written to
• read a Gmsh mesh file
• double nodes along a path defined by the user
• modify the solid elements involved and
• generate interface elements

14. Some application examples

15. Path following method
Riks 1972 load factor
Newton-Raphson
f ext = g
where
!(u, ) arc-length/constraint function
uI = K1r, uII = K1g
correction
reference load vector

16. Energy control
✏ = Ba BT
Gutierrez 2004 equilibrium
V =
1
2
Z
⌦
✏T =
1
2
Z
⌦
aTBT =
1
2
aTf int =
1
2
aTg
Energy release rate a˙Tg
˙V
f int =
Z
⌦
Arc-length function
predefined amount of energy
to be released [Nm]
forward Euler
G 0

17. Assumption: secant unloading!!!
E
straight line

18. Indirect displacement
control [de Borst 1986]
imagine what if
there are 2 cracks???
SEN beam
Indirect displacement control
(||uA uB|| ,l) local quantity!!!

19. Advantages of
energy control SEN beam
Energy control
- fast to evaluate
- global quantity
multiple cracks
FP van der Mer
EFM, 2008

20. Solution procedure
load
control
energy control
FP van der Mer
EFM, 2008

21. f int + f coh

22. Numerical examples
• Simple tests (to debug code)
• Material interface debonding
• Multi-delamination of a composite DCB
• Delamination of the DCB

23. Debonding of a
material interface
interface: linear 4-node
continuum: T3 elements
Cohesive law: Xu-Needleman

24. Simple test
plane strain

25. Multi-delamination

26. Multi-delamination

27. Matrix kinking
interface elements everywhere
except for the hard inclusion
“Discontinuous Galerkin/extrinsic cohesive zone modeling: Implementation caveats and applications in
computational fracture mechanics”, VP Nguyen, Engineering Fracture Mechanics, 2014.

28. Final remarks
• Basic of interface elements was introduced
• Energy control path-following method was presented
When crack path is not known...
interface elements
inserted a priori at
every element edges!!!

29. Things to explore
• New cohesive laws
• New (better) interface element formulations
(current element technology does not allow
industrial applications to be realized.)
• Mesh topology such that mesh bias can be avoided.