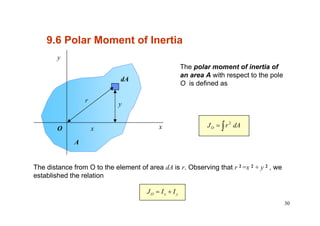
This document discusses moments of inertia, which are a measure of an object's resistance to rotational acceleration about an axis. It defines the moment of inertia of an area and introduces key concepts like the parallel axis theorem, radius of gyration, and calculating moments of inertia through integration or for composite areas. Examples are provided to demonstrate calculating moments of inertia for various shapes, including rectangles, triangles, L-shapes, and composite profiles, about different axes. The document also covers determining moments of inertia at the centroidal axes versus other axes using the parallel axis theorem.

1. 1
CHAPTER 9:
Moments of Inertia
! Moment of Inertia of Areas
! Second Moment, or Moment of Inertia, of an
Area
! Parallel-Axis Theorem
! Radius of Gyration of an Area
! Determination of the Moment of Inertia of an
Area by Integration
! Moments of Inertia of Composite Areas
! Polar Moment of Inertia

2. 2
9.1 Moment of Inertia: Definition
x
y
y
x
dA=(dx)(dy)
∫=
A
x dAyI 2
)(
O
∫=
A
y dAxI 2
)(

3. 3
x
y
x´= Centroidal axis
y´ = Centroidal axis
CG
dy
y´
dx x´
dA
∫ +=
A
yx dAdyI 2
)'(
∫ ++=
A
yy dAddyy ])())('(2)'[( 22
∫∫∫ ++=
A
y
A
y
A
dAddAdydAy 22
)())('(2)'(
∫∫ ++=
A
y
A
yx dAddAydI
2
'2
0, y´ = 0
AdII yxx
2
0 ++=
AdII xyy
2
0 ++=
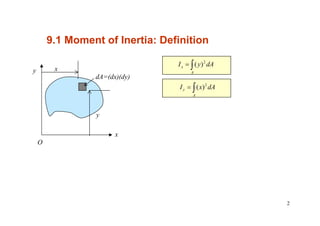
9.2 Parallel-Axis Theorem of an Area
2
AdJJ CO +=
O

4. 4
y
x
kx
O
A
A
J
k
A
I
k
A
I
k O
O
y
y
x
x ===
9.3 Radius of Gyration of an Area
2
The radius of gyration of an area
A with respect to the x axis is
defined as the distance kx, where
Ix = kx A. With similar definitions for
the radii of gyration of A with
respect to the y axis and with
respect to O, we have

5. 5
The rectangular moments of inertia Ix
and Iy of an area are defined as
These computations are reduced to single integrations by choosing dA to be a thin
strip parallel to one of the coordinate axes. The result is
x
y
y
dx
x
∫∫ == dAxIdAyI yx
22
dxyxdIdxydI yx
23
3
1
==
9.4 Determination of the Moment of Inertia of an
Area by Integration

6. 6
x´
y´
b/2
h/2
• Moment of Inertia of a Rectangular Area.
x
y
b
h
y
dy
∫=
A
x dAyI 2
∫=
h
bdyy
0
2
)(
h
by
0
3
3
)(
=
y
dy
∫==
A
xx dAyII 2
'
∫=
h
dy
b
y
0
2
)
2
(4
2/
0
3
3
)
2
(4
h
yb
=
3
3
bh
=
12
3
bh
=
dA = bdy
dA = (b/2)dy

7. 7
x´
y´
b/2
h/2
x
y b
h
∫=
A
y dAxI 2
∫=
b
hdxx
0
2
)(
b
hx
0
3
3
)(
=
∫==
A
yy dAxII 2
'
∫=
h
dx
h
x
0
2
)
2
(4
2/
0
3
3
)
2
(4
b
xh
=
3
3
hb
=
12
3
hb
=
x
dx
x
dx
dA = hdx
dA = (h/2)dx

8. 8
x
y
b
h/2
h/2
12
3
bh
Ix =
3
3
bh
Ix =
2
AdII xx +=
2
3
)
2
)((
12
h
bh
bh
+=
412
33
bhbh
+=
3
3
bh
Ix =

9. 9
dIx = y2 dA dA = l dy
Using similar triangles, we have
dy
h
yh
bdA
h
yh
bl
h
yh
b
l −
=
−
=
−
=
Integrating dIx from y = 0 to y = h, we obtain
∫∫
∫
−=
−
=
=
hh
x
dyyhy
h
b
dy
h
yh
by
dAyI
0
32
0
2
2
)(
12
]
43
[
3
0
43
bhyy
h
h
b h
=−=
• Moment of Inertia of a Triangular Area.
2
AdII xx +=
36
)
3
)(
2
(
12
3
2
3
2
bhhbhbh
AdII xx
=−=
−=
y
x
h
b/2
h-y
b/2
dy
yl

10. 10
Example 9.1
Determine the moment of inertia of the shaded area shown with respect to
each of the coordinate axes.
x
y
a
y = kx2
b

11. 11
x
y
a
y = kx2
b
• Moment of Inertia Ix.
dy
dA = (a-x)dy
2
kxy =
2
kab =
2
a
b
k =
2/1
2/1
2
2
y
b
a
xorx
a
b
y ==
Substituting x = a and y=b
∫=
A
x dAyI 2
∫ −=
b
dyxay
0
2
)(
∫ −=
b
dyy
b
a
ay
0
2/1
2/1
2
)(
dyy
b
a
dyya
bb
∫∫ −=
0
2/5
2/1
0
2
bb
y
b
aay
0
2/7
2/1
0
3
)
7
2
(
3
−=
)
7
2
(
3
2/7
2/1
3
b
b
aab
−=
7
2
3
33
abab
−=
21
3
ab
=

12. 12
x
y
a
y = kx2
b
• Moment of Inertia Iy.
2
2
x
a
b
y = ∫=
A
y dAxI 2
∫=
a
ydxx
0
2
dx
dA = ydx
∫=
a
dxx
a
b
x
0
2
2
2
)(
∫=
a
dxx
a
b
0
4
2
a
x
a
b
0
5
2
)
5
)((=
)
5
)((
5
2
a
a
b
=
5
3
ba
=

13. 13
Example 9.2
Determine the moment of inertia of the shaded area shown with respect to
each of the coordinate axes.
x
y
y2 = x2
y1 = x
(a,b)

14. 14
x
y
y2 = x2
y1 = x
(a,b)
dy
dA = (x2 - x1)dy
∫=
A
x dAyI 2
∫ −=
b
dyxxy
0
2
)( 12
∫ −=
b
dyyyy
0
2/12
)(
∫∫ −=
bb
dyydyy
0
3
0
2/5
)()(
bb
y
y
0
4
0
2/7
47
2
−=
• Moment of Inertia Ix.
47
2 4
2/7 b
b −=

15. 15
x
y
y2 = x2
y1 = x
(a,b)
• Moment of Inertia Iy.
∫=
A
y dAxI 2
∫ −=
a
dxyyx
0
1
2
)( 2
dx
dA = (y1 - y2)dx
∫ −=
a
dxxxx
0
22
)(
∫∫ −=
aa
dxxdxx
0
4
0
3
)()(
aa
xx
0
5
0
4
54
−=
54
54
aa
−=

16. 16
The parallel-axis theorem is used very effectively to compute the moment of
inertia of a composite area with respect to a given axis.
d
c
o
centroid are related to the distance d between points C and O by the relationship
2
AdJJ CO +=
9.5 Moment of Inertia of Composite Areas
A similar theorem can be used with
the polar moment of inertia. The
polar moment of inertia
JO of an area about O and the polar
moment of inertia JC of the area
about its

17. 17
Example 9.3
Compute the moment of inertia of the composite area shown.
75 mm
75 mm
100 mm
25 mm
x

18. 18
SOLUTION
75 mm
75 mm
100 mm
x
25 mm
= (dy)Cir
Ciryxctx AdI
bh
I )()
3
(
2
Re
3
+−=
Circt ])75)(25()25(
4
1
[])150)(100(
3
1
[ 224
Re
3
×+−= ππ
= 101x106 mm4

19. 19
Example 9.4
Determine the moments of inertia of the beam’s cross-sectional area
shown about the x and y centroidal axes.
400
Dimension in mm
100
400
100
600
100
x
y
C

20. 20
400
Dimension in mm
100
400
100
600
100
x
y
C
SOLUTION
A
dyA
B
dyD
D
CyxByxAyxx AdIAdIAdII )()()(
222
+++++=
])200)(300100()300)(100(
12
1
[
]0)100)(600(
12
1
[])200)(300100()300)(100(
12
1
[
23
323
×++
++×+=
= 2.9x109 mm4
0

21. 21
400
Dimension in mm
100
400
100
600
100
x
y
C
CxyBxyAxyy AdIAdIAdII )()()(
222
+++++=
C
BA
])250)(300100()100)(300(
12
1
[
]0)600)(100(
12
1
[])250)(300100()100)(300(
12
1
[
23
323
×++
++×+=
= 5.6x109 mm4
A
dxA
dxD
D
0

22. 22
Example 9.5 (Problem 9.31,33)
Determine the moments of inertia and the radius of gyration of the
shaded area with respect to the x and y axes.
6 mm
O x
y
24 mm
24 mm
6 mm
12 mm12 mm
24 mm 24 mm
8 mm

23. 23
6 mm
O
x
y
24 mm
24 mm
6 mm
12 mm12 mm
24 mm 24 mm
8 mm
SOLUTION
A
dyA
B
Ix = 390x103 mm4
mm
A
I
k x
x 9.21
)]648()488()624[(
10390 3
=
×+×+×
×
==
CyxByxAyxx AdIAdIAdII )()()(
222
+++++=
Iy = 64.3x103 mm4
CBA ])48)(6(
12
1
[])8)(48(
12
1
[])24)(6(
12
1
[ 333
++=
0 00
CxyBxyAxyy AdIAdIAdII )()()(
222
+++++=
mm
A
I
k
y
y 87.8
)]648()488()624[(
103.64 3
=
×+×+×
×
==
0
C
B
A
])27)(648()6)(48(
12
1
[
]0)48)(8(
12
1
[
])27)(624()6)(24(
12
1
[
23
3
23
×++
++
×+=
C
dyC

24. 24
Example 9.6 (Problem 9.32,34)
Determine the moments of inertia and the radius of gyration of the
shaded area with respect to the x and y axes.
2 m
O
1 m
1 m
1 m
1 m
0.5 m0.5 m
2 m 2 m
0.5 m0.5 m
x
y

25. 25
2 m
O
1 m
1 m
1 m
1 m
0.5 m0.5 m 2 m 2 m
0.5 m0.5 m
x
y
A
B
dyB
C
dyC
Ix = 46 m4
m
A
I
k x
x 599.1
)]14()24()65[(
46
=
×−×−×
==
14
2
24
2
65
2
)()()( ××× +−+−+= CyxByxAyxx AdIAdIAdII
0
C
BA
])5.1)(14()1)(4(
12
1
[
])2)(42()2)(4(
12
1
[]0)6)(5(
12
1
[
23
233
×+−
×+−+=
Iy = 46.5 m4
CBA ])4)(1(
12
1
[])4)(2(
12
1
[])5)(6(
12
1
[ 333
−−=
0 00
CxyBxyAxyy AdIAdIAdII )()()(
222
+−+−+=
m
A
I
k
y
y 607.1
)]14()24()65[(
5.46
=
×−×−×
==

26. 26
Example 9.7
Determine the moments of inertia and the radius of gyration of the
shaded area with respect to the x and y axes and at the centroidal axes.
1 cm 1 cm
5 cm
1 cm
5 cm
x
y

27. 27
1 cm 1 cm
5 cm
1 cm
5 cm
x
y
CG
Y
∑∑ = AyAY
cm
Y
5.2
)15(3
)51)(5.0()]15)(5.3[(2
=
×
×+×
=
4
2
2
25.51
)5.2)(15(145
cm
AdII yxx
=
−=
−=
• Moments of inertia about centroid
4
23
23
25.51
])2)(15()1)(5(
12
1
[(
])1)(15()5)(1(
12
1
[(2
cm
I
OR
x
=
×++
×+=
cm
A
I
kk x
yx 848.1
15
25.51
====
4
323
145
)1)(5(
3
1
])5.3)(15()5)(1(
12
1
[(2
cm
Ix
=
+×+=
• Moments of inertia about x axis
4
323
25.51
)5)(1(
12
1
])2)(15()1)(5(
12
1
[(2
cm
II yy
=
+×+==
0.5
3.5
2

28. 28
Example 9.8
The strength of a W360 x 57 rolled-steel beam is increased by attaching a
229 mm x 19 mm plate to its upper flange as shown. Determine the
moment of inertia and the radius of gyration of the composite section with
respect to an axis which is parallel to the plate and passes through the
centroid C of the section.
C
229 mm
19 mm
358 mm
172 mm

29. 29
229 mm
172 mm
SOLUTION
19 mm
358 mm x
O
C x´
Y
188.5 mm
The wide-flange shape of W360 x 57
found by referring to Fig. 9.13
A = 7230 mm2 4
2.160 mmIx =
AyAY Σ=Σ
Aplate = (229)(19) = 4351 mm2
)7230)(0()4351)(5.188()72304351( +=+Y
mmY 8.70=
• Centroid
• Moment of Inertia
flangewidexplatexx III −+= )()( '''
flangewidexplatex YAIAdI −+++= )()( 2
'
2
'
[ ]
46
26
23
108.256
)8.70)(7230(102.160
)8.705.188)(4351()19)(229(
12
1
mm×=
+×+




−+=
• Radius of Gyration
)72304351(
108.256 6
'2
'
+
×
==
A
I
k x
x
mmkx 149' =
46
' 10257 mmIx ×=
d

30. 30
The polar moment of inertia of
an area A with respect to the pole
O is defined as
The distance from O to the element of area dA is r. Observing that r 2 =x 2 + y 2 , we
established the relation
y
xx
y
r
A
dA
O ∫= dArJO
2
yxO IIJ +=
9.6 Polar Moment of Inertia

31. 31
Example 9.9
(a) Determine the centroidal polar moment of inertia of a circular area by
direct integration. (b) Using the result of part a, determine the moment of
inertia of a circular area with respect to a diameter.
y
x
r
O

32. 32
u
du
O
y
x
r
SOLUTION
a. Polar Moment of Inertia.
duudAdAudJO π22
==
∫∫ ∫ ===
rr
OO duuduuudJJ
0
3
0
2
2)2( ππ
4
2
rJO
π
=
b. Moment of Inertia with Respect to a Diameter.
xyxO IIIJ 2=+=
xIr 2
2
4
=
π
4
4
rII xdiameter
π
==