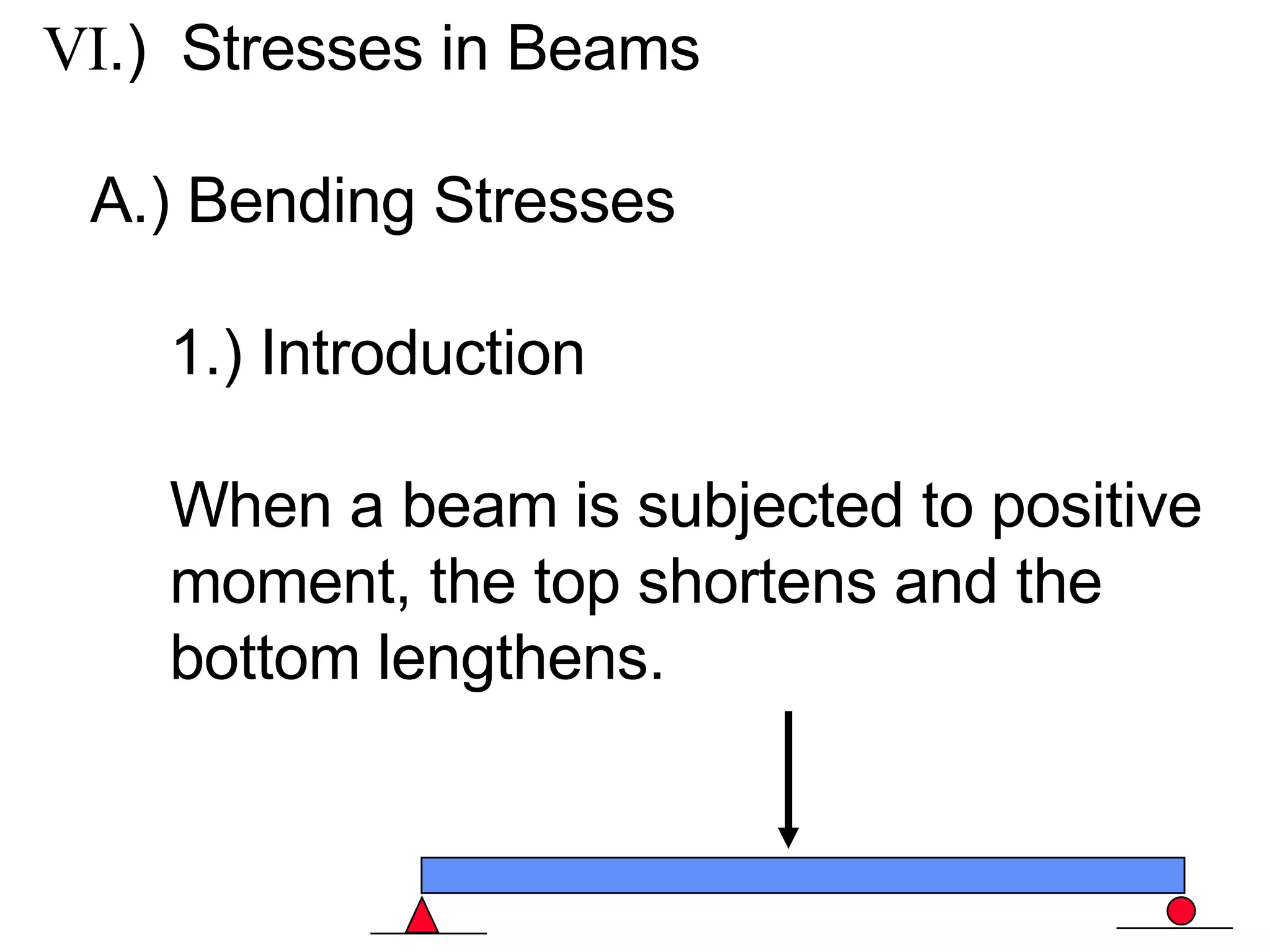
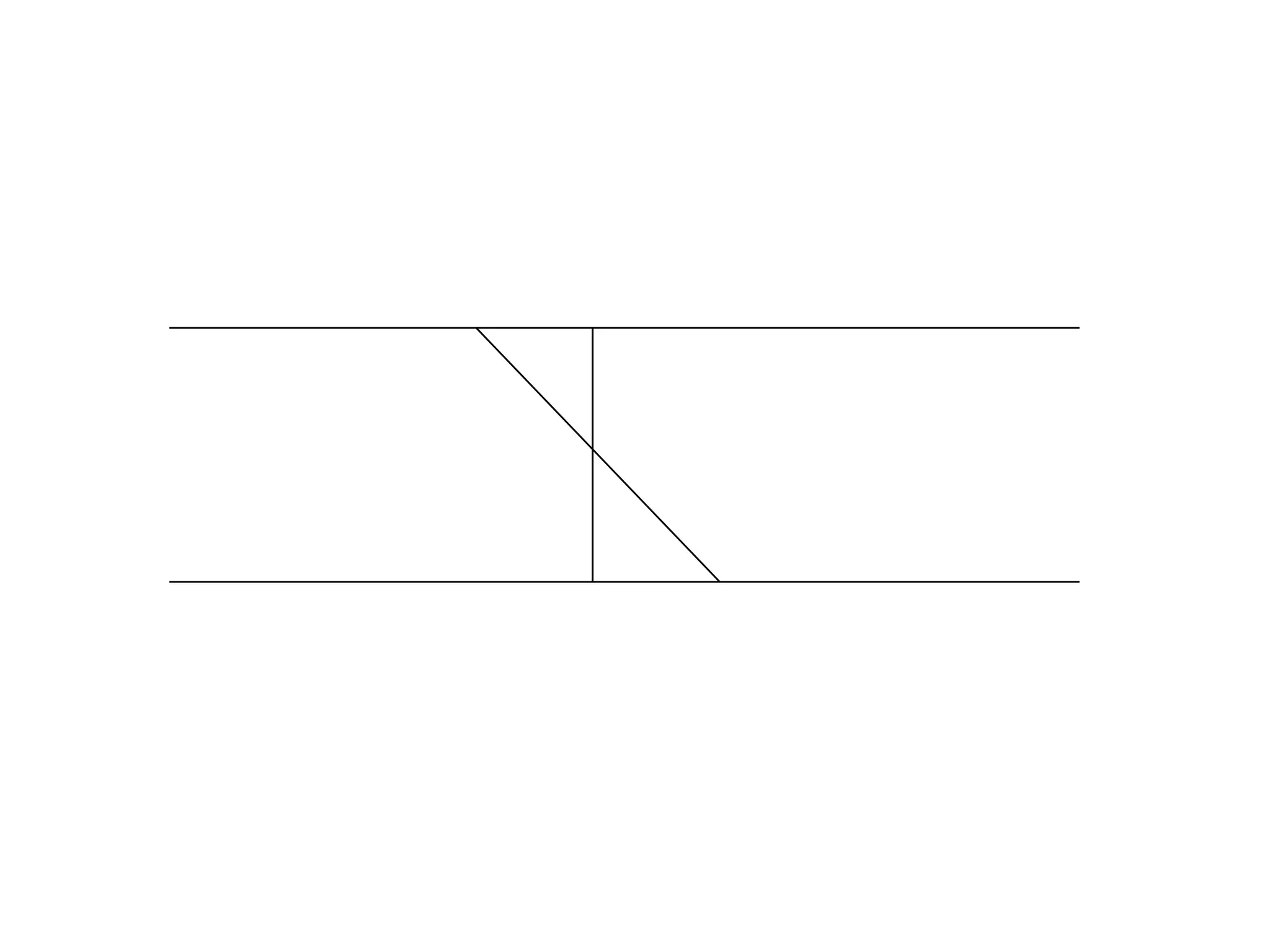
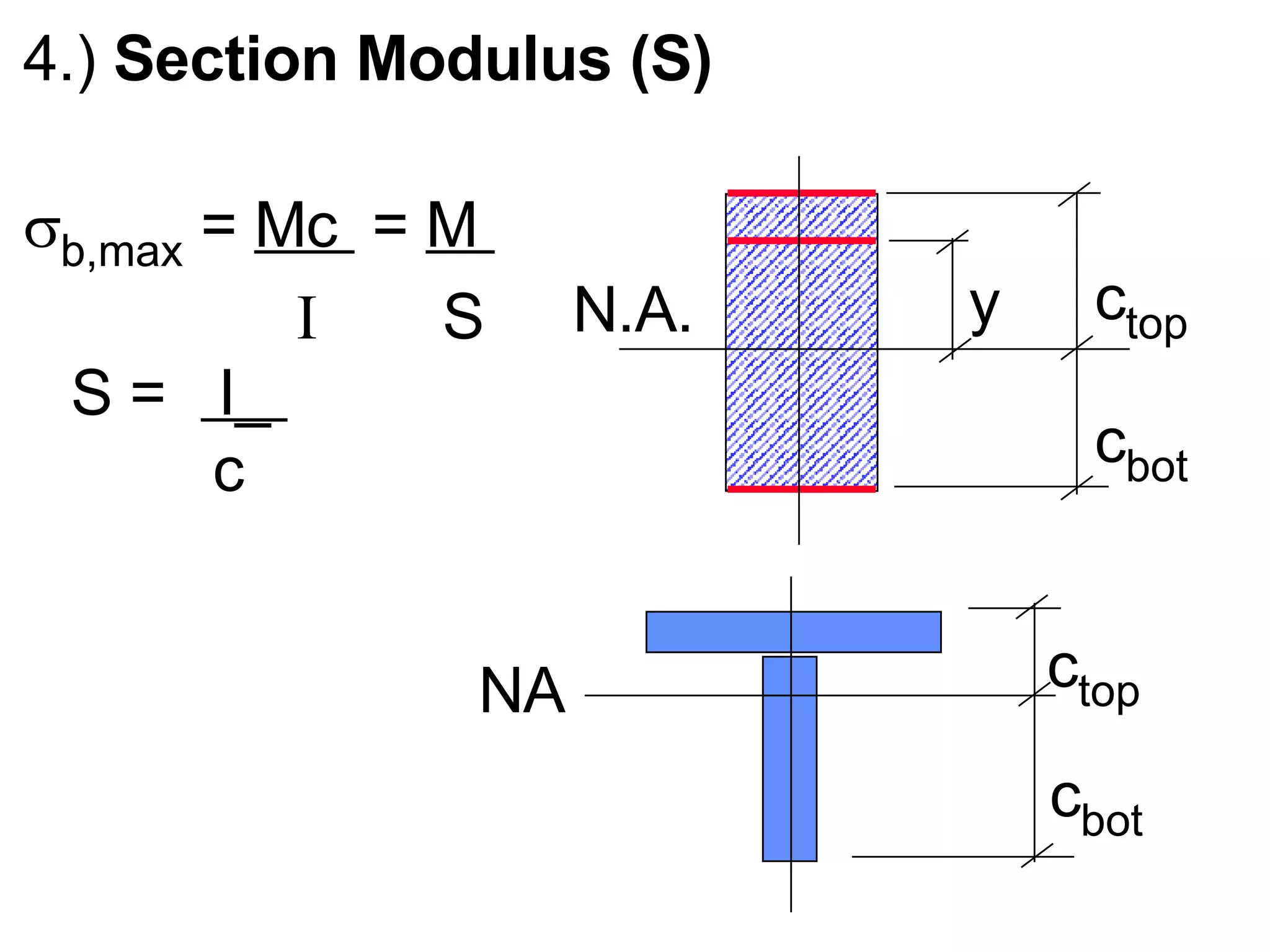
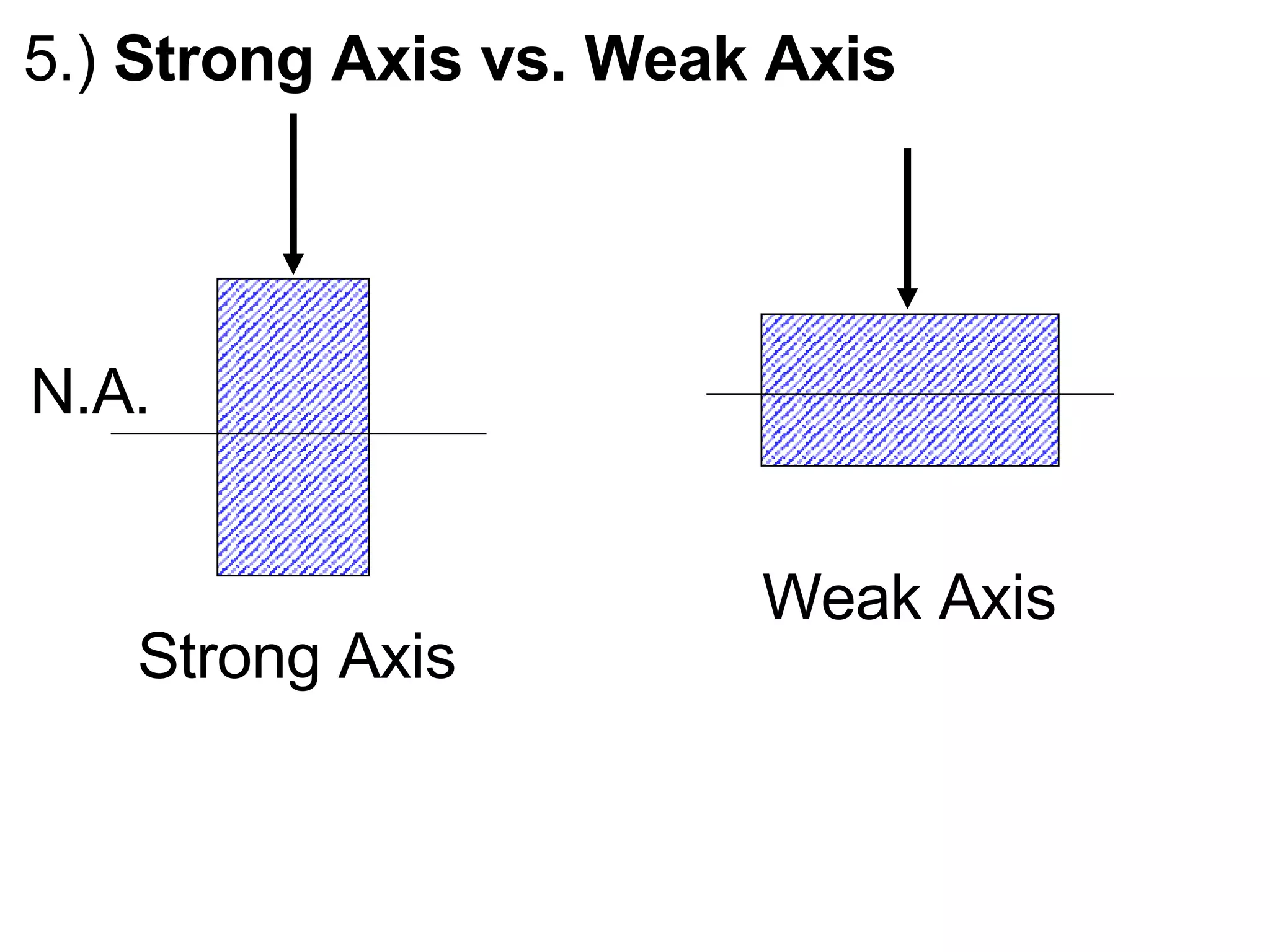
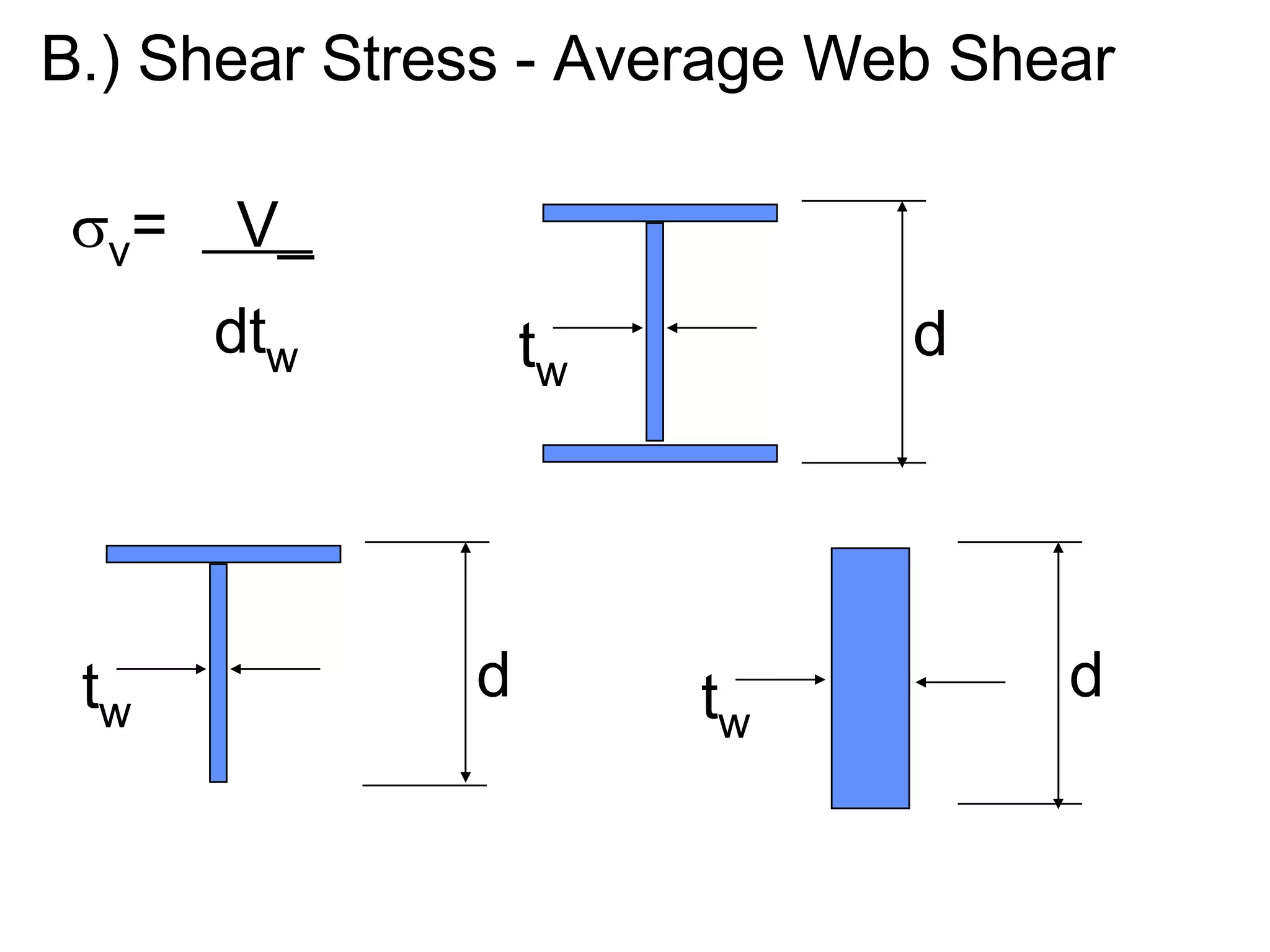
The document discusses stresses in beams, including: 1) Bending stresses are highest at the outer fibers of the beam and zero at the neutral axis, following the bending strains. The flexure formula relates bending stress to moment, distance from neutral axis, and moment of inertia. 2) Maximum bending stress occurs at the outer fibers and can be calculated using the section modulus, which relates to moment of inertia and distance from neutral axis to outer fibers. 3) Beams have a strong axis and weak axis based on their moment of inertia.

1. VI .) Stresses in Beams A.) Bending Stresses 1.) Introduction When a beam is subjected to positive moment, the top shortens and the bottom lengthens.

3. The bending strains are zero at the neutral axis. The bending strains increase proportionately with the distance from the neutral axis. The maximum strains occur at the top and bottom of the beam (outer fibers)

4. Since stress is directly related to strain  =  E), bending stress is also zero at the neutral axis and increases with the distance from the neutral axis. The maximum bending stresses occur at the top and bottom of the beam (outer fibers)

5. 2.) The Flexure Formula  b = My I   b = Bending stress at a distance “y” from the neutral axis (ksi). y = distance from the neutral axis (in). M = Moment at a given cross-section of a beam (k-in). I = Moment of inertia of the cross- section (in 4 ). N.A. y

6. 3.) Maximum Bending Stress  b,max = Mc I  b,max = Maximum bending stress at a given cross-section (ksi). c = Distance from N.A. to the outer fibers of cross-section (in) M, I = as defined before. N.A. c top c bot y

7. 4.) Section Modulus (S)  b,max = Mc = M I S S = I_ c N.A. c top c bot y NA c top c bot

8. 5.) Strong Axis vs. Weak Axis Strong Axis N.A. Weak Axis

9. B.) Shear Stress - Average Web Shear  v = V_ dt w d t w d t w d t w

10. C.) The Beam Shear Stress Formula  v = VQ Ib V = Shear force (lb) Q = First Moment of Area I = 2 nd Moment of Inertia(in 4 ) b = thickness (in) at the location where shear is being computed

11. C.) The Beam Shear Stress Formula Q = First Moment about the neutral axis of the area between the horizontal plane where the shear is to be calculated and the top or bottom of the beam. Plane where shear Is being computed Neutral axis y Q = Ay

12. C.) The Beam Shear Stress Formula  v = 1.5V for solid rectangular cross-sections A  v = 4V for solid circular cross-sections 3A