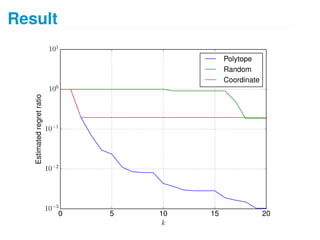
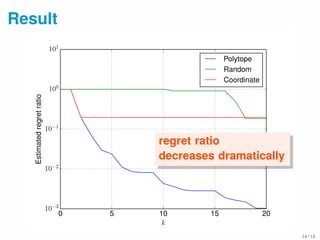
This document presents algorithms for minimizing regret ratio in multi-objective submodular function maximization. It introduces the concept of regret ratio for evaluating the quality of a solution set for multiple objectives. It then proposes two algorithms, Coordinate and Polytope, that provide upper bounds on regret ratio by leveraging approximation algorithms for single objective problems. Experimental results on a movie recommendation dataset show the proposed algorithms achieve significantly lower regret ratios than a random baseline.

1. Regret Ratio Minimization in
Multi-objective Submodular
Function Maximization
P(S)
a
Tasuku Soma (U. Tokyo)
with Yuichi Yoshida (NII & PFI)
1 / 15

2. Submodular Func. Maximization
f : 2E
→ R+ is submodular:
f(X + e) − f(X) ≥ f(Y + e) − f(Y) (X ⊆ Y, e ∈ E Y)
“diminishing return”
max f(X)
s.t. X ∈ C
Applications
• Influence Maximization
• Data Summarization,
etc
2 / 15

3. Multiple Criteria
3 / 15

4. Multiple Criteria
3 / 15

5. Multiple Criteria
1. coverage
3 / 15

6. Multiple Criteria
1. coverage
2. diversity
3 / 15

7. Multi-objective Optimization?
× Exponentially Many Pareto Solutions!
4 / 15

8. Multi-objective Optimization?
× Exponentially Many Pareto Solutions!
“Good” Subsets of Pareto Solutions
• k-representative skyline queries [Lin et al. 07,
Tao et al. 09]
• top-k dominating queries [Yiu and Mamoulis 09]
• regret minimizing database [Nanongkai et al. 10]
4 / 15

9. Multi-objective Optimization?
× Exponentially Many Pareto Solutions!
“Good” Subsets of Pareto Solutions
• k-representative skyline queries [Lin et al. 07,
Tao et al. 09]
• top-k dominating queries [Yiu and Mamoulis 09]
• regret minimizing database [Nanongkai et al. 10]
Issue These assume data points are explicitly given...
4 / 15

10. Our Results
Extend regret ratio framework to submodular maximization
5 / 15

11. Our Results
Extend regret ratio framework to submodular maximization
Upper Bound
Given an α-approx algorithm for (weighted) single
objective problem,
• regret ratio 1 − α/d for any d
• regret ratio 1 − α + O(1/k) for any k and d = 2.
d = # objectives, k = # of feasible solutions
5 / 15

12. Our Results
Extend regret ratio framework to submodular maximization
Upper Bound
Given an α-approx algorithm for (weighted) single
objective problem,
• regret ratio 1 − α/d for any d
• regret ratio 1 − α + O(1/k) for any k and d = 2.
d = # objectives, k = # of feasible solutions
Lower Bound
• Even if α = 1 and d = 2, it is impossible to achieve
regret ratio o(1/k2
).
5 / 15

13. Regret Ratio
Single Objective
The regret ratio for S ⊆ C and f is
rr(S) = 1 −
maxX∈S f(X)
maxX∈C f(X)
.
6 / 15

14. Regret Ratio
Single Objective
The regret ratio for S ⊆ C and f is
rr(S) = 1 −
maxX∈S f(X)
maxX∈C f(X)
.
Multi Objective
The regret ratio for S ⊆ C and f1, . . ., fd is
rrf1,...,fd,C(S) = max
a∈Rd
+
rrfa,C(S),
where fa := a1f1 + · · · + adfd. (linear weighting)
6 / 15

15. Geometry of Regret Ratio
f1
f2
Pareto opt point
7 / 15

16. Geometry of Regret Ratio
f1
f2
Pareto opt point
P(S)
point in S
7 / 15

17. Geometry of Regret Ratio
f1
f2
Pareto opt point
P(S)
point in S
ε−1
P(S)
rr(S) ≤ 1 − ε ⇐⇒ f(X) ∈ ε−1
P(S) (X ∈ C).
7 / 15

18. Regret Ratio Minimization
Given: f1, . . ., fd: submodular, C ⊆ 2E
, k > 0
minimize rr(S)
subject to S ⊆ C, |S| ≤ k.
8 / 15

19. Algorithm 1: Coordinate
f1
f2
approx solution to
maxX∈C f1(X)
approx solution to
maxX∈C f2(X)
Scoord: α-approx. solutions to maxX∈C fi(X) (i = 1, . . ., d)
=⇒ rr(Scoord) ≤ 1 − α/d.
9 / 15

20. Algorithm 2: Polytope
f1
f2
a: normal vector
10 / 15

21. Algorithm 2: Polytope
f1
f2
approx solution to
maxX∈C fa(X)
10 / 15

22. Algorithm 2: Polytope
f1
f2
10 / 15

23. Algorithm 2: Polytope
f1
f2
10 / 15

24. Algorithm 2: Polytope
f1
f2
S: output of Coordinate and d = 2,
=⇒ rr(S) ≤ 1 − α − O(1/k).
10 / 15

25. Lower Bound
f1(X) = cos
π|X|
2n
, f2(X) = sin
π|X|
2n
> π
2k
f1
f2
distance = O(1/k2
)
11 / 15

26. Experiment
Algorithms
• Coordinate
• Polytope
• Random: Pick k random directions a1, . . ., ak and
output the family {X1, . . ., Xk } of solutions, where Xi
is an approx solution to max
X∈C
fai
(X).
Machine
• Intel Xeon E5-2690 (2.90 GHz) CPU, 256 GB RAM
• implemented in C#
12 / 15

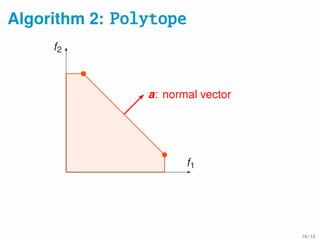
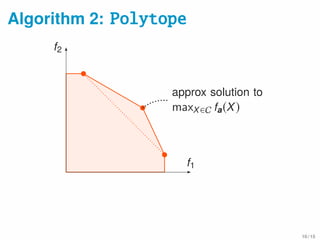
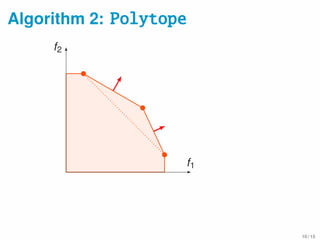
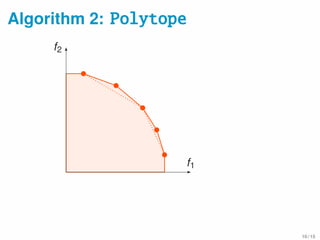
27. Data Summarization
Dataset: MovieLens
E: set of movies, si,j: similarities of movies i and j
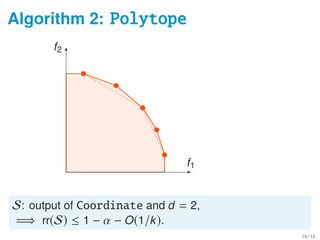
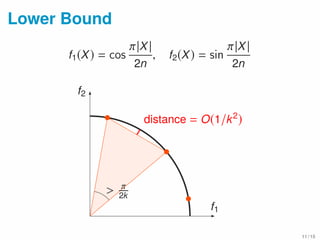
f1(X) =
i∈E j∈X
si,j, coverage
f2(X) = λ
i∈E j∈E
si,j − λ
i∈X j∈X
si,j diversity
C = 2E
(unconstrained), 1 ≤ k ≤ 20, λ > 0,
single-objective algorithm: double greedy (1/2-approx)
[Buchbinder et al. 12]
13 / 15

28. Result
0 5 10 15 20
k
10−3
10−2
10−1
100
101
Estimatedregretratio
Polytope
Random
Coordinate

29. Result
0 5 10 15 20
k
10−3
10−2
10−1
100
101
Estimatedregretratio
Polytope
Random
Coordinate
regret ratio
decreases dramatically
14 / 15

30. Our Results
Extend regret ratio framework to submodular maximization
Upper Bound
Given an α-approx algorithm for (weighted) single
objective problem,
• regret ratio 1 − α/d for any d
• regret ratio 1 − α + O(1/k) for any k and d = 2.
d = # objectives, k = # of feasible solutions
Lower Bound
• Even if α = 1 and d = 2, it is impossible to achieve
regret ratio o(1/k2
).
15 / 15