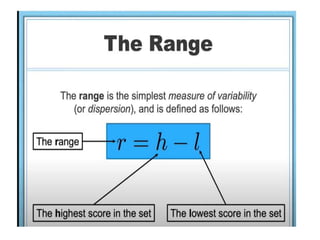
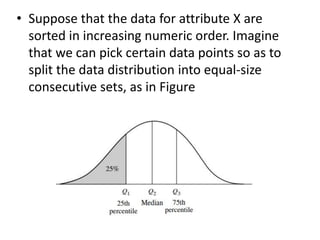
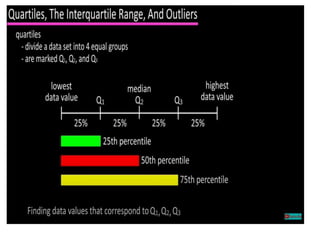
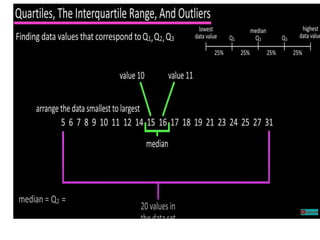
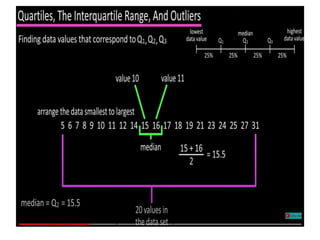
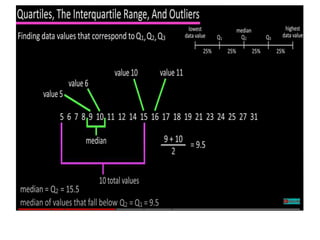
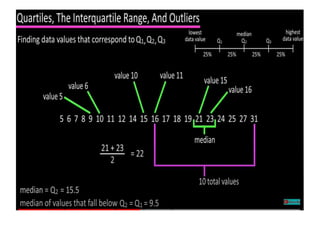
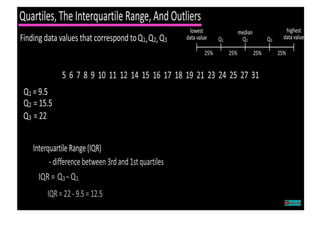
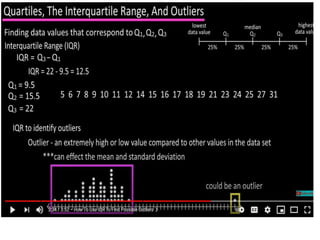
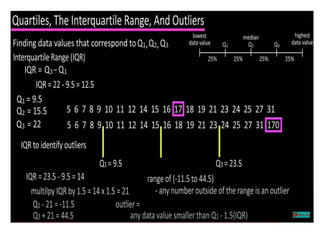
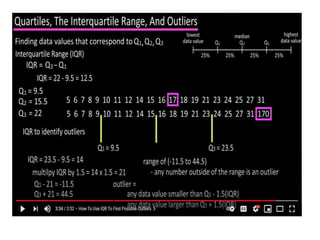
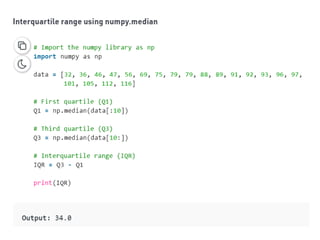
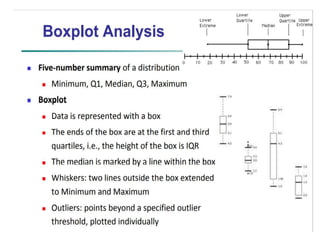
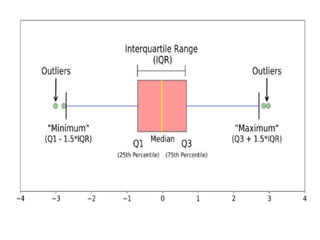
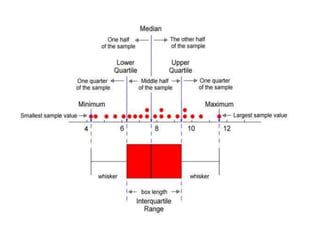
The document discusses the concepts of range, quartiles, and interquartile range (IQR) in data analysis, providing examples of calculation from a given data set. It explains how to determine the median, first quartile, and third quartile, and how the IQR is used for creating box plots and identifying outliers. Additionally, a comparison of interquartile ranges in different data sets is presented, emphasizing that a lower IQR indicates preferable data variability.

1. Range, Quartiles, and Interquartile Range
M.Swarna Sudha
Assistant Professor(Senior Grade)
Department of CSE
Ramco Institute of Technology
CS8075 DATA WAREHOUSING AND DATA MINING

2. Range, Quartiles, and Interquartile
Range
• Let x1,x2,...,xN be a set of observations for
some numeric attribute, X.
• The range of the set is the difference between
the largest (max()) and smallest (min()) values

5. • Suppose that the data for attribute X are
sorted in increasing numeric order. Imagine
that we can pick certain data points so as to
split the data distribution into equal-size
consecutive sets, as in Figure

16. Examples
• 75, 69, 56, 46, 47, 79, 92, 97, 89, 88, 36, 96, 105, 32, 116,
101, 79, 93, 91, 112
• After sorting the above data set:
32, 36, 46, 47, 56, 69, 75, 79, 79, 88, 89, 91, 92, 93, 96, 97,
101, 105, 112, 116
• Here the total number of terms is 20.
• The second quartile (Q2) or the median of the above data is
(88 + 89) / 2 = 88.5
• The first quartile (Q1) is median of first n i.e. 10 terms (or n
i.e. 10 smallest values) = 62.5
• The third quartile (Q3) is the median of n i.e. 10 largest
values (or last n i.e. 10 values) = 96.5
• Then, IQR = Q3 – Q1 = 96.5 – 62.5 = 34.0

18. • The IQR is used to build box plots, simple graphical
representations of a probability distribution.
• The IQR can also be used to identify the outliers in the
given data set.
• The IQR gives the central tendency of the data.
Decision Making
• The data set has a higher value of interquartile range
(IQR) has more variability.
• The data set having a lower value of interquartile
range (IQR) is preferable.
• Suppose if we have two data sets and their
interquartile ranges are IR1 and IR2, and if IR1 > IR2
then the data in IR1 is said to have more variability
than the data in IR2 and data in IR2 is preferable.
USE of IQR