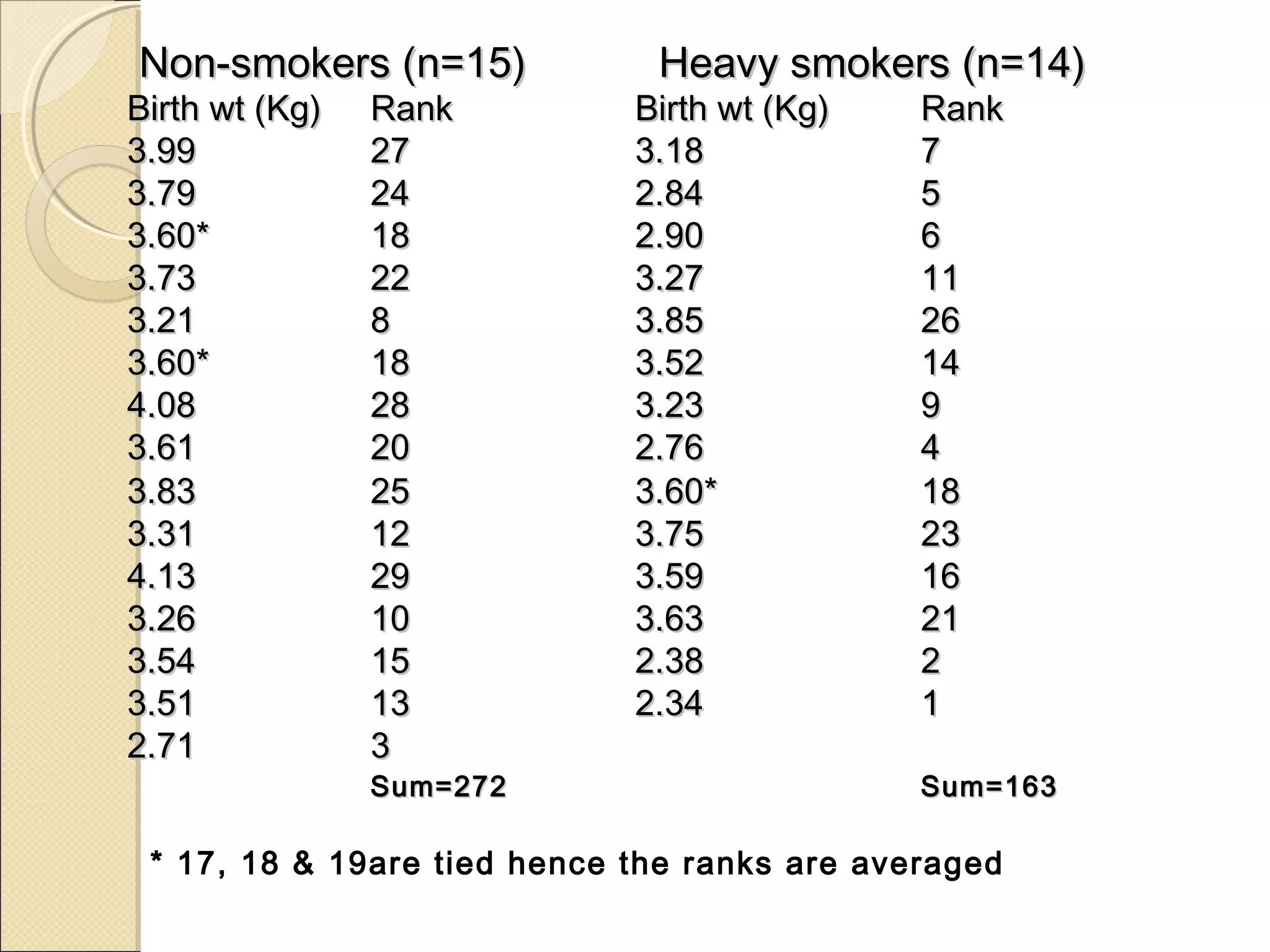
The Wilcoxon signed-rank test is a non-parametric statistical test used to compare two related samples or repeated measurements on a single sample to assess if their population mean ranks differ. It can be used as an alternative to the paired t-test when the population cannot be assumed to be normally distributed. The test involves ranking the differences between paired observations, ignoring the signs of the differences, and comparing the sum of the ranks of the positive or negative differences to critical values to determine if there are statistically significant differences between the samples. A limitation is that observations with a difference of zero are discarded, which can be a concern if samples come from a discrete distribution.

1. welcomewelcome

2. The Wilcoxon signed-rank test is a non-parametric
statistical hypothesis test used when comparing two related
samples, matched samples, or repeated measurements on a
single sample to assess whether their population mean
ranks differ (i.e. it is a paired difference test). It can be used
as an alternative to the paired Student's t-test, t-test for
matched pairs, or the t-test for dependent samples when
the population cannot be assumed to be normally
distributed.[1]
A Wilcoxon signed-rank test is a
nonparametric test that can be used to determine whether
two dependent samples were selected from populations

3. Wilcoxon signed rank testWilcoxon signed rank test
To test difference between paired
data

4. Orginal test:
The original Wilcoxon's proposal used a
different statistic. Denoted by Siegel as
the T statistic, it is the smaller of the two
sums of ranks of given sign; in the example
given below, therefore, T would equal
3+4+5+6=18. Low values of T are required
for significance. As will be obvious from
the example below, T is easier to calculate by
hand than W and the test is equivalent to the
two-sided test described above; however, the
distribution of the statistic under has to be
adjusted

5. STEP 1STEP 1
Exclude any differences which are zero
Put the rest of differences in ascending order
Ignore their signs
Assign them ranks
If any differences are equal, average their
ranks

6. STEP 2STEP 2
Count up the ranks of +ives as T+
Count up the ranks of –ives as T-

7. STEP 3STEP 3
If there is no difference between drug (T+) and
placebo (T-), then T+ & T- would be similar
If there were a difference
one sum would be much smaller and
the other much larger than expected
The smaller sum is denoted as T
T = smaller of T+ and T-

8. STEP 4STEP 4
Compare the value obtained with the
critical values (5%, 2% and 1% ) in table
N is the number of differences that
were ranked (not the total number of
differences)
So the zero differences are excluded

9. PatientPatient
Hours of sleepHours of sleep
DifferenceDifference
RankRank
Ignoring signIgnoring sign
DrugDrug PlaceboPlacebo
11 6.16.1 5.25.2 0.90.9 3.5*3.5*
22 7.07.0 7.97.9 -0.9-0.9 3.5*3.5*
33 8.28.2 3.93.9 4.34.3 1010
44 7.67.6 4.74.7 2.92.9 77
55 6.56.5 5.35.3 1.21.2 55
66 8.48.4 5.45.4 3.03.0 88
77 6.96.9 4.24.2 2.72.7 66
88 6.76.7 6.16.1 0.60.6 22
99 7.47.4 3.83.8 3.63.6 99
1010 5.85.8 6.36.3 -0.5-0.5 11
3rd
& 4th
ranks are tied hence averaged
T= smaller of T+ (50.5) and T- (4.5)
Here T=4.5 significant at 2% level indicating the drug (hypnotic) is
more effective than placebo

10. Wilcoxon rank sum testWilcoxon rank sum test
To compare two groups
Consists of 3 basic steps

11. Non-parametric equivalent ofNon-parametric equivalent of
t testt test

12. Step 1Step 1
Rank the data of both the groups in
ascending order
If any values are equal average
their ranks

13. Step 2Step 2
Add up the ranks in group with
smaller sample size
If the two groups are of the same
size either one may be picked
T= sum of ranks in group with
smaller sample size

14. Step 3Step 3
Compare this sum with the critical ranges
given in table
Look up the rows corresponding to the
sample sizes of the two groups
A range will be shown for the 5%
significance level

15. Non-smokers (n=15)Non-smokers (n=15) Heavy smokers (n=14)Heavy smokers (n=14)
Birth wt (Kg)Birth wt (Kg) RankRank Birth wt (Kg)Birth wt (Kg) RankRank
3.993.99 2727 3.183.18 77
3.793.79 2424 2.842.84 55
3.60*3.60* 1818 2.902.90 66
3.733.73 2222 3.273.27 1111
3.213.21 88 3.853.85 2626
3.60*3.60* 1818 3.523.52 1414
4.084.08 2828 3.233.23 99
3.613.61 2020 2.762.76 44
3.833.83 2525 3.60*3.60* 1818
3.313.31 1212 3.753.75 2323
4.134.13 2929 3.593.59 1616
3.263.26 1010 3.633.63 2121
3.543.54 1515 2.382.38 22
3.513.51 1313 2.342.34 11
2.712.71 33
Sum=272Sum=272 Sum=163Sum=163
* 17, 18 & 19are tied hence the ranks are averaged

16. Limitation[edit]
As demonstrated in the example, when the
difference between the groups is zero, the
observations are discarded. This is of
particular concern if the samples are taken
from a discrete distribution. In these
scenarios the modification to the Wilcoxon
test by Pratt 1959, provides an alternative
which incorporates the zero differences.[4]
[5]
This modification is more robust for data
on an ordinal scale