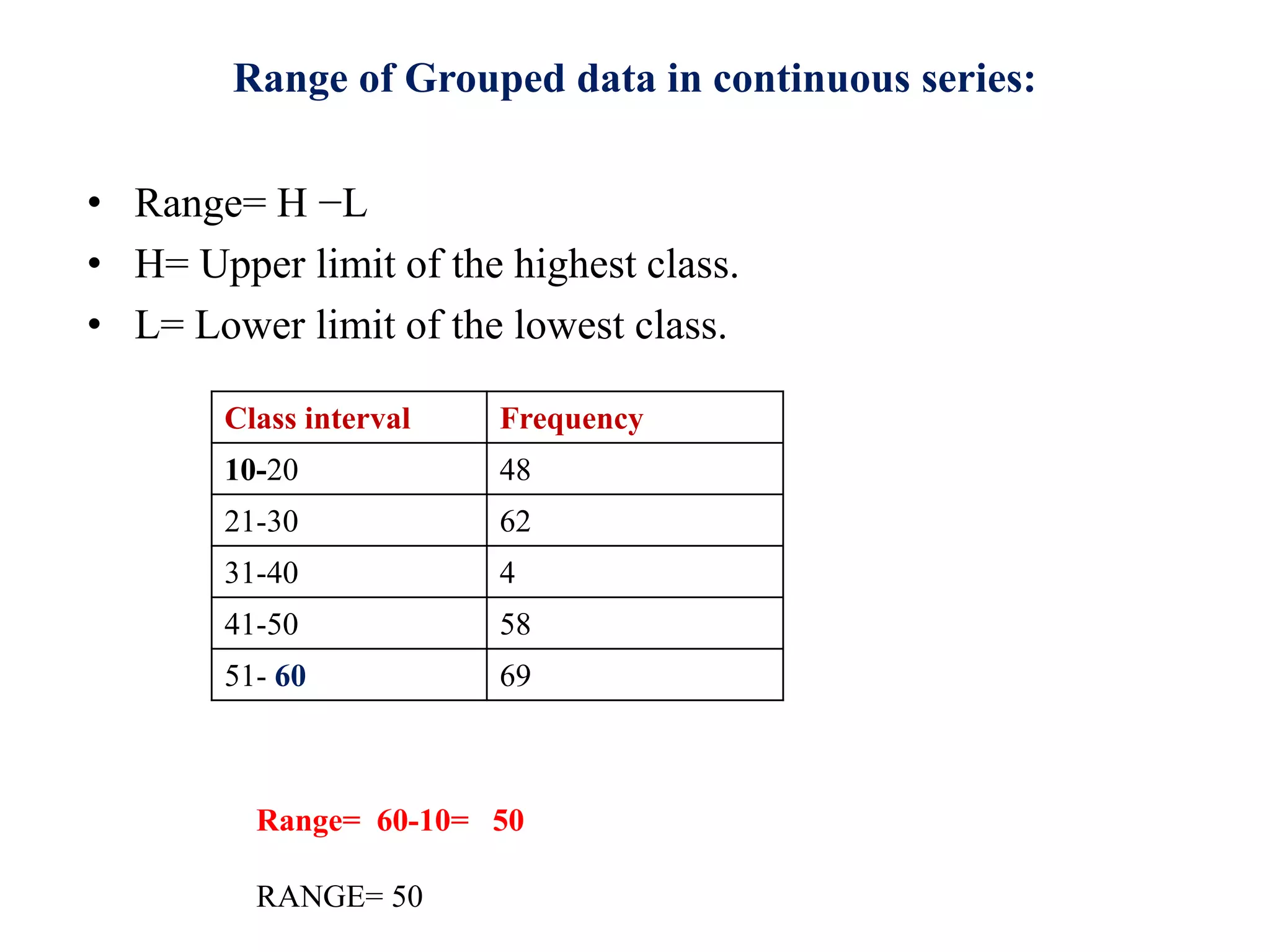
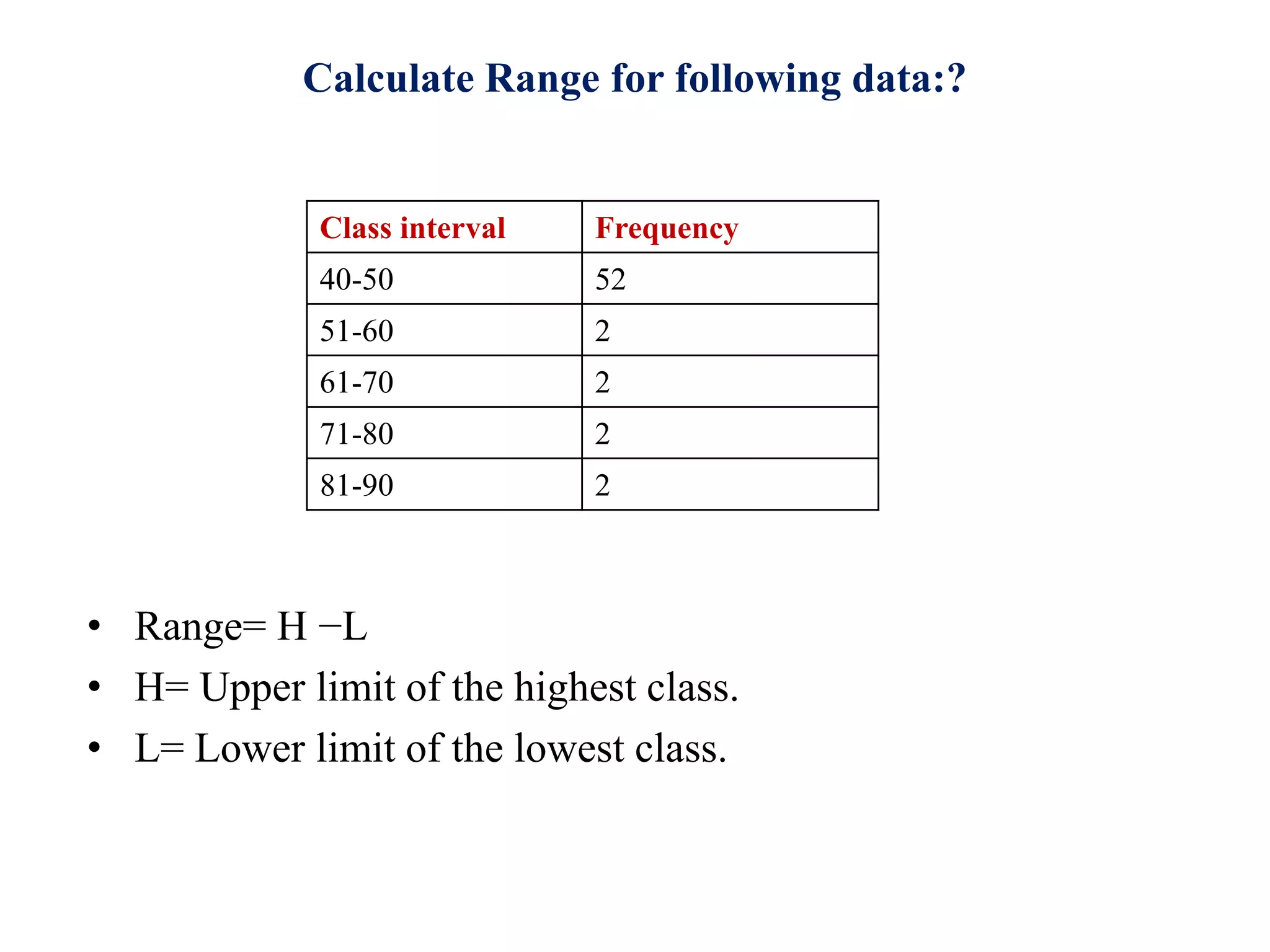
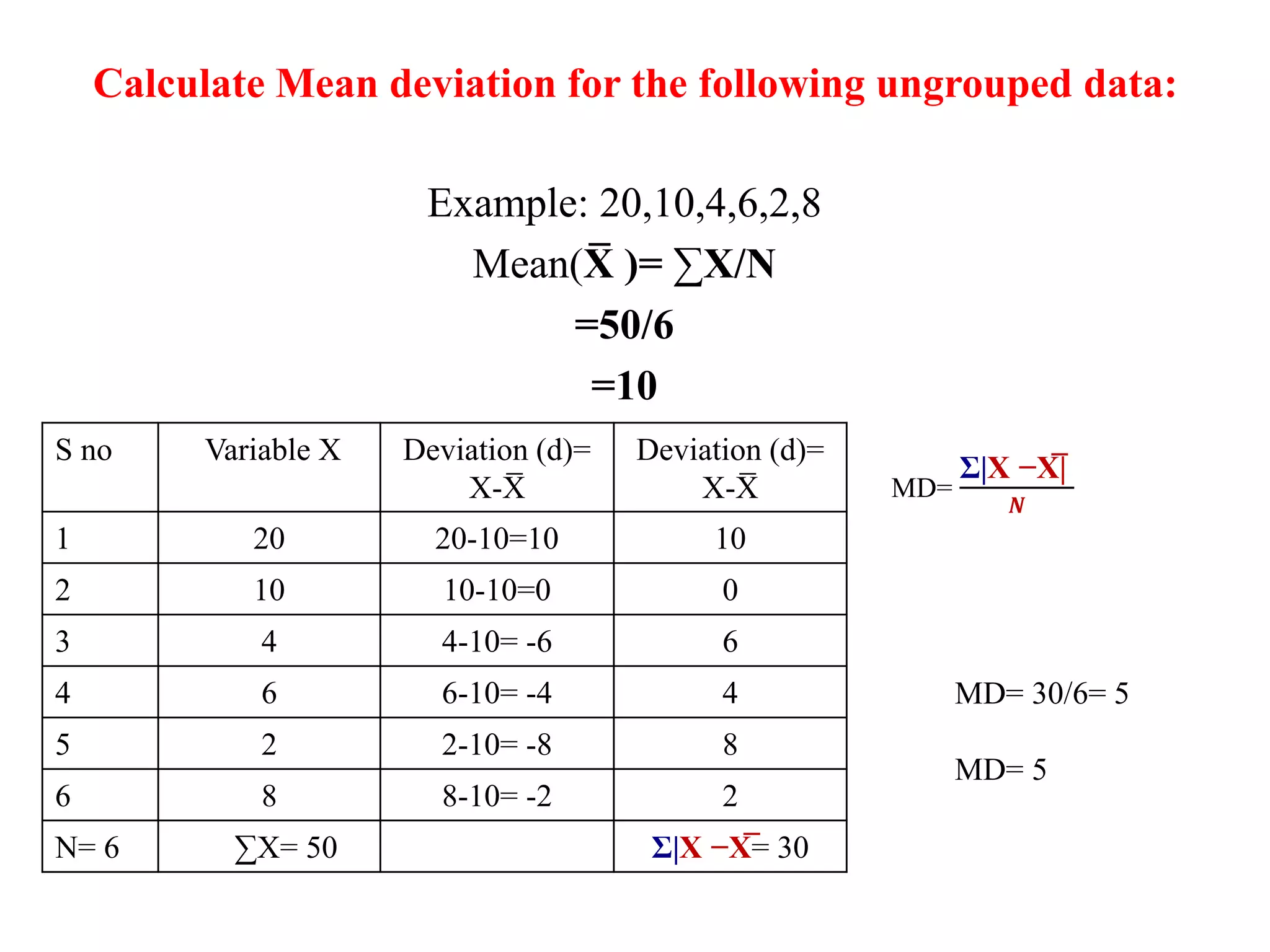
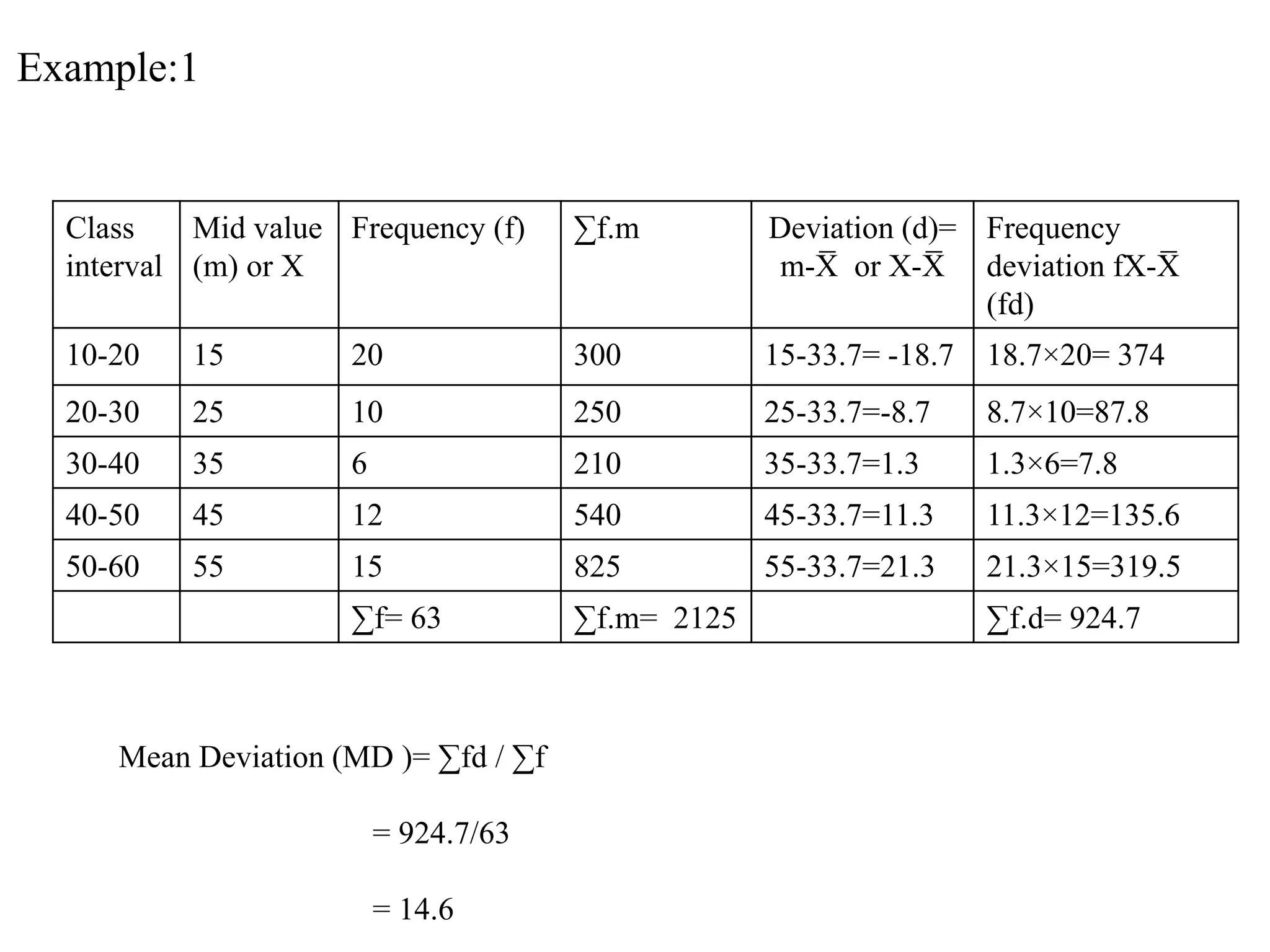
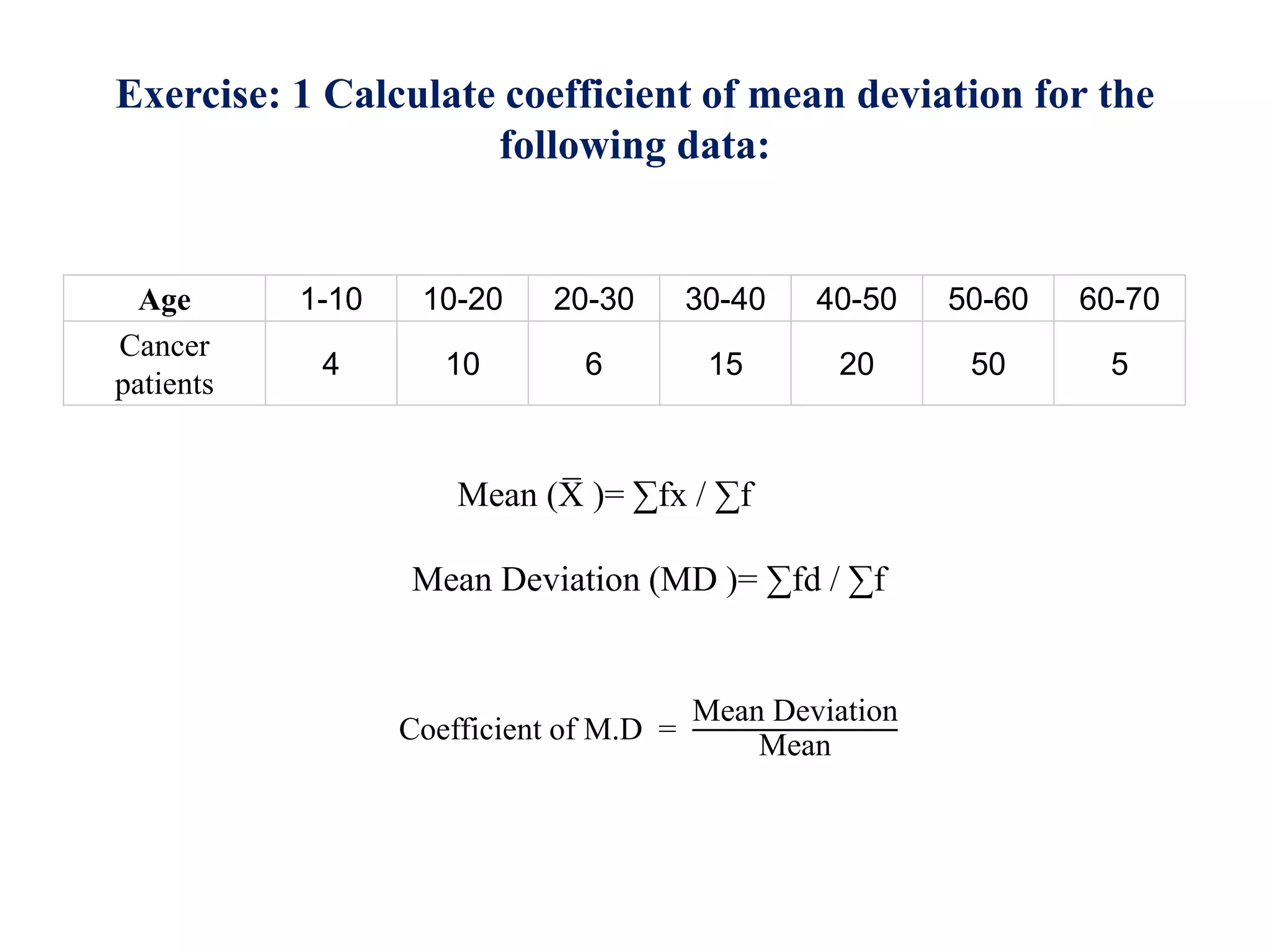
The document discusses various measures of dispersion for data, including range, mean deviation, and coefficient of mean deviation. Range is defined as the difference between the highest and lowest values in a data set. Mean deviation is the average of the deviations from the mean. Coefficient of mean deviation is a relative measure of dispersion calculated by dividing the mean deviation by the mean. Examples are provided to demonstrate calculating these measures for both ungrouped and grouped data. The measures are used to analyze variation in data sets from fields like medicine, weather, and business.

1. Measures of dispersion
Dr. Harinatha Reddy Aswartha
Department of Life Sciences

2. Range:

3. Range:
• The Range is the difference between the highest and smallest values
in a set of observations.
Range: Large value in the series of data − Smallest value in the series data.
R= L −S
• Example:
141, 112, 125, 100, 115, 122, 150,
Arrange the data in ascending order: 100,112, 115,122,125,141,150.
Highest value: 150
Smallest value: 100
Range: 150-100= 50

4. Example: Calculate range for the following ungrouped data:
• 100, 112, 125, 135, 150, 152, 150, 155, 160, 130,128, 138,
133, 143, 147, 151, 154, 156, 112, 116.

5. Range of Grouped data in continuous series:
• Range= H −L
• H= Upper limit of the highest class.
• L= Lower limit of the lowest class.
Class interval Frequency
10-20 48
21-30 62
31-40 4
41-50 58
51- 60 69
Range= 60-10= 50
RANGE= 50

6. Calculate Range for following data:?
• Range= H −L
• H= Upper limit of the highest class.
• L= Lower limit of the lowest class.
Class interval Frequency
40-50 52
51-60 2
61-70 2
71-80 2
81-90 2

7. Coefficient of Range:

8. Coefficient of Range:
• The measure of the distribution based on range is the
coefficient of range also known as range coefficient of
dispersion.
• Coefficient of range is the relative measure corresponding to
range.
• Coefficient range=
• H= Highest value,
• L= Lowest value,

9. Coefficient of Range for the following data:
• 100,50,30,20,70,40,10,70
• Coefficient of Range:
= 100-10/100+10
= 90/110
= 0.81
= 81%

10. Calculate Range and coefficient range for the following data:
Example:
48, 60, 50, 36, 69, 51, 51, 38, 40, 41, 46, 45, 53, 41, 46, 45, 60.

11. Uses of Range
• Range observations is important in analysing the variations in
the quality of products, like medicines, antibiotics, tonics etc.
• Range is useful measure in the study of fluctuations in
maximum and minimum temperature and humidity are used
for weather forecast.

12. Mean deviation
150

13. Mean deviation:
• Mean deviation: can be defined as the mean of all the
deviations in a given set of data obtained from an average.
• Formula for ungrouped data:
Mean deviation (MD):
Σ|X −X̅|
𝑵
X= Variable or Value of the observation
X̅: Arithmetic mean or mean or Average
N: Total number of observations
X-X̅ (d): Deviation

14. Calculate Mean deviation for the following ungrouped data:
Example: 20,10,4,6,2,8
Mean(X
̅ )= ∑X/N
=50/6
=10
MD=
Σ|X −X̅|
𝑵
S no Variable X Deviation (d)=
X-X
̅
Deviation (d)=
X-X
̅
1 20 20-10=10 10
2 10 10-10=0 0
3 4 4-10= -6 6
4 6 6-10= -4 4
5 2 2-10= -8 8
6 8 8-10= -2 2
N= 6 ∑X= 50 Σ|X −X̅= 30
MD= 30/6= 5
MD= 5

15. Calculate mean deviation for following ungrouped data:
Examples: 5,10,20,2,10,20 ?

16. Mean deviation for grouped data (Continuous series)
• Mean Deviation (MD )= ∑fd / ∑f
• ∑fd = Sum of multiplication of each frequency and deviation
form mean.
• ∑f= Sum of all the frequency.

17. Example:1
Age H1N1 patients
10-20 20
20-30 10
30-40 6
40-50 12
50-60 15

18. Example:1
Mean (X
̅ )= ∑f.m / ∑f
= 2125/63=
= 33.7
Age Mid value (m) HIV cases (f) ∑f.m
10-20 15 20 300
20-30 25 10 250
30-40 35 6 210
40-50 45 12 540
50-60 55 15 825
∑f= 63 ∑f.m= 2125

19. Example:1
Class
interval
Mid value
(m) or X
Frequency (f) ∑f.m Deviation (d)=
m-X
̅ or X-X
̅
Frequency
deviation fX-X
̅
(fd)
10-20 15 20 300 15-33.7= -18.7 18.7×20= 374
20-30 25 10 250 25-33.7=-8.7 8.7×10=87.8
30-40 35 6 210 35-33.7=1.3 1.3×6=7.8
40-50 45 12 540 45-33.7=11.3 11.3×12=135.6
50-60 55 15 825 55-33.7=21.3 21.3×15=319.5
∑f= 63 ∑f.m= 2125 ∑f.d= 924.7
Mean Deviation (MD )= ∑fd / ∑f
= 924.7/63
= 14.6

20. Example:2: Find mean deviation for the following data:
Age HBV patients
0-5 8
5-10 5
10-15 6
15-20 2
20-25 10

21. Uses of mean deviation:
• Mean deviation used in medicine, microbiology,
pharmacology, social sciences and in business etc.
• Mean deviation is good for sample studies where
detailed study is not required.

22. Coefficient of mean deviation

23. • A relative measure of dispersion based on the mean
deviation is called the coefficient of the mean deviation or the
coefficient of dispersion.
• The coefficient of mean deviation is calculated by dividing
mean deviation by the average (Mean).
Coefficient of M.D =
Mean Deviation
Mean
Coefficient of the mean deviation:

24. Calculate coefficient of mean deviation for the following grouped
data:
Age 3-4 4-5 5-6 6-7 7-8 8-9 9-10
Diabetes
PATIENTS
3 7 22 60 85 32 8
Mean Deviation (MD )= ∑fd / ∑f
Mean (X
̅ )= ∑fm / ∑f
Coefficient of M.D =
Mean Deviation
Mean

25. Class
interv
al
Middle
value
(m or
X)
Freque
ncy (f)
fm Deviation (d)=
m-X
̅
(Step: 2)
Frequency
deviation (fd)
(Step: 3)
3-4 3.5 3 10.5 3.5-7.09= 3.59 3×3.59=10.77
4-5 4.5 7 31.5 4.5-7.09=2.59 4.5×2.59=18.13
5-6 5.5 22 121. 1.59 34.98
6-7 6.5 60 390 0.59 35.40
7-8 7.5 85 637.5 0.41 34.85
8-9 8.5 32 272. 1.41 45.12
9-10 9.5 8 76 2.41 19.28
∑f=217 ∑fm=1538.5 ∑fd=198.53
Step:1
Mean (X
̅ )= ∑fm / ∑f
= 1538.5/217
Mean X
̅ = 7.09
Step:4
Mean Deviation (MD )= ∑fd / ∑f
= 198.53/217
= 0.915
Step:5
C.E of M.D =
Mean Deviation
Mean
= 0.915/7.09
= 0.129

26. Exercise: 1 Calculate coefficient of mean deviation for the
following data:
Age 1-10 10-20 20-30 30-40 40-50 50-60 60-70
Cancer
patients
4 10 6 15 20 50 5
Mean Deviation (MD )= ∑fd / ∑f
Mean (X
̅ )= ∑fx / ∑f
Coefficient of M.D =
Mean Deviation
Mean

27. THANK YOU