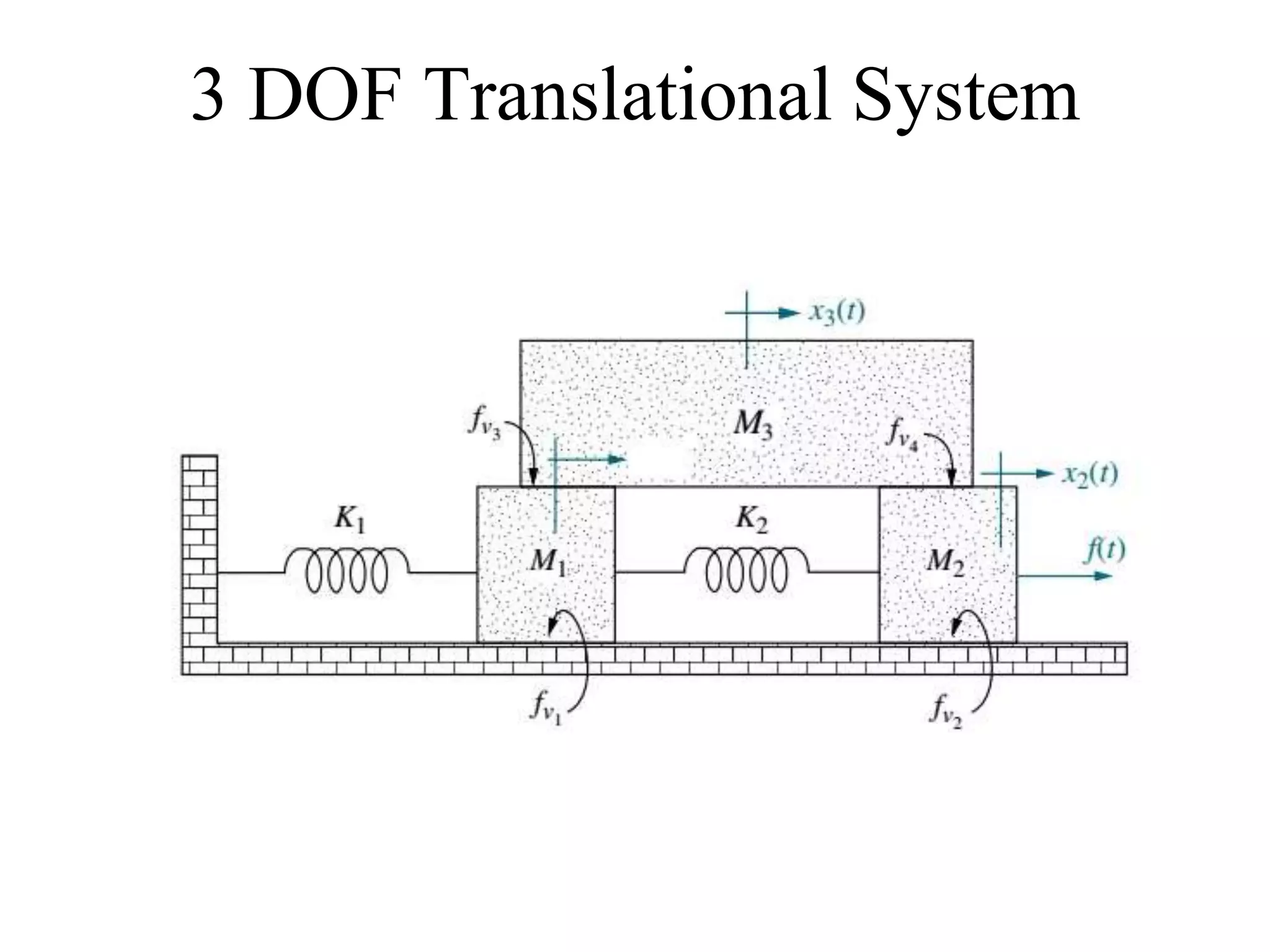
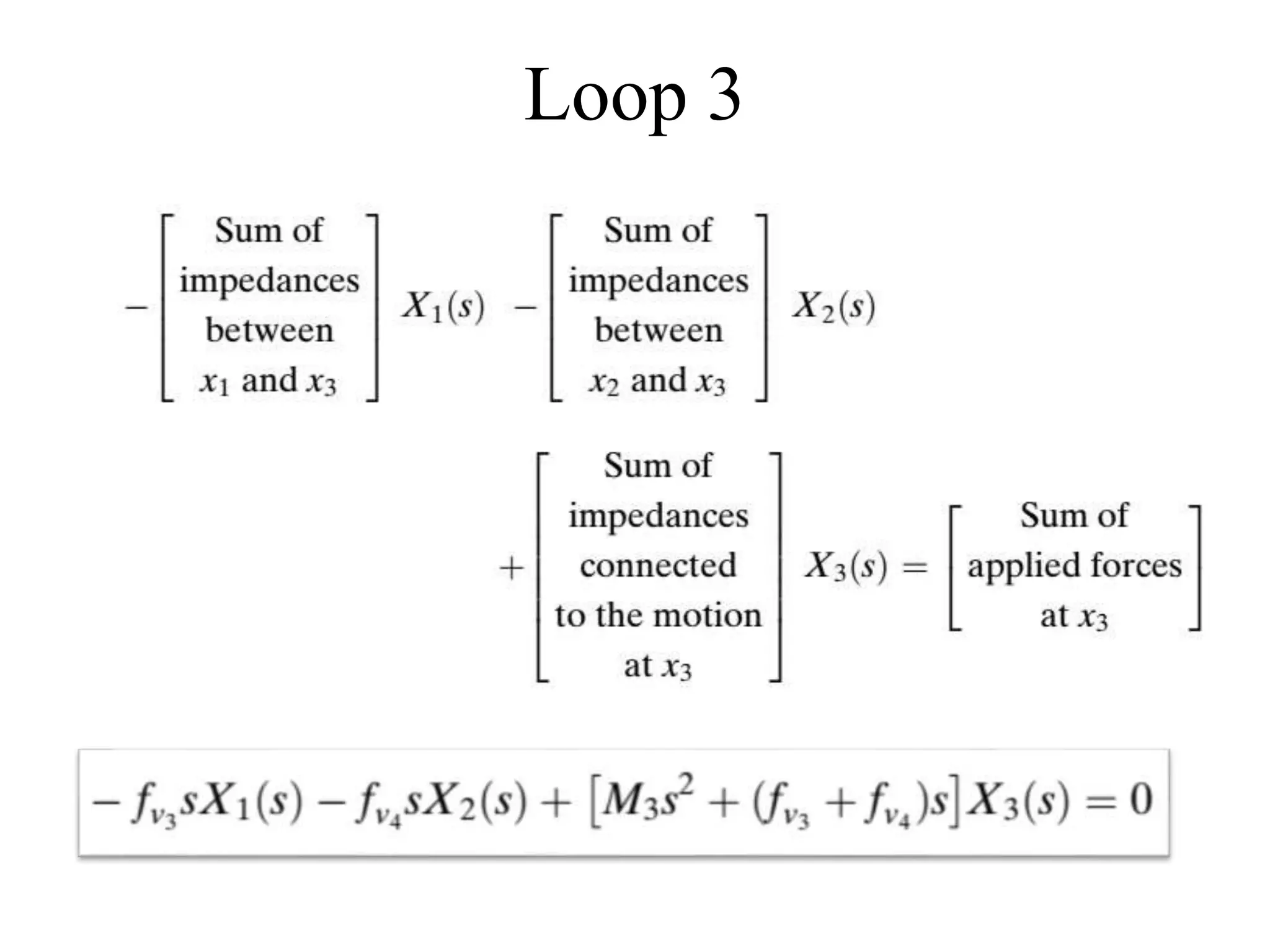
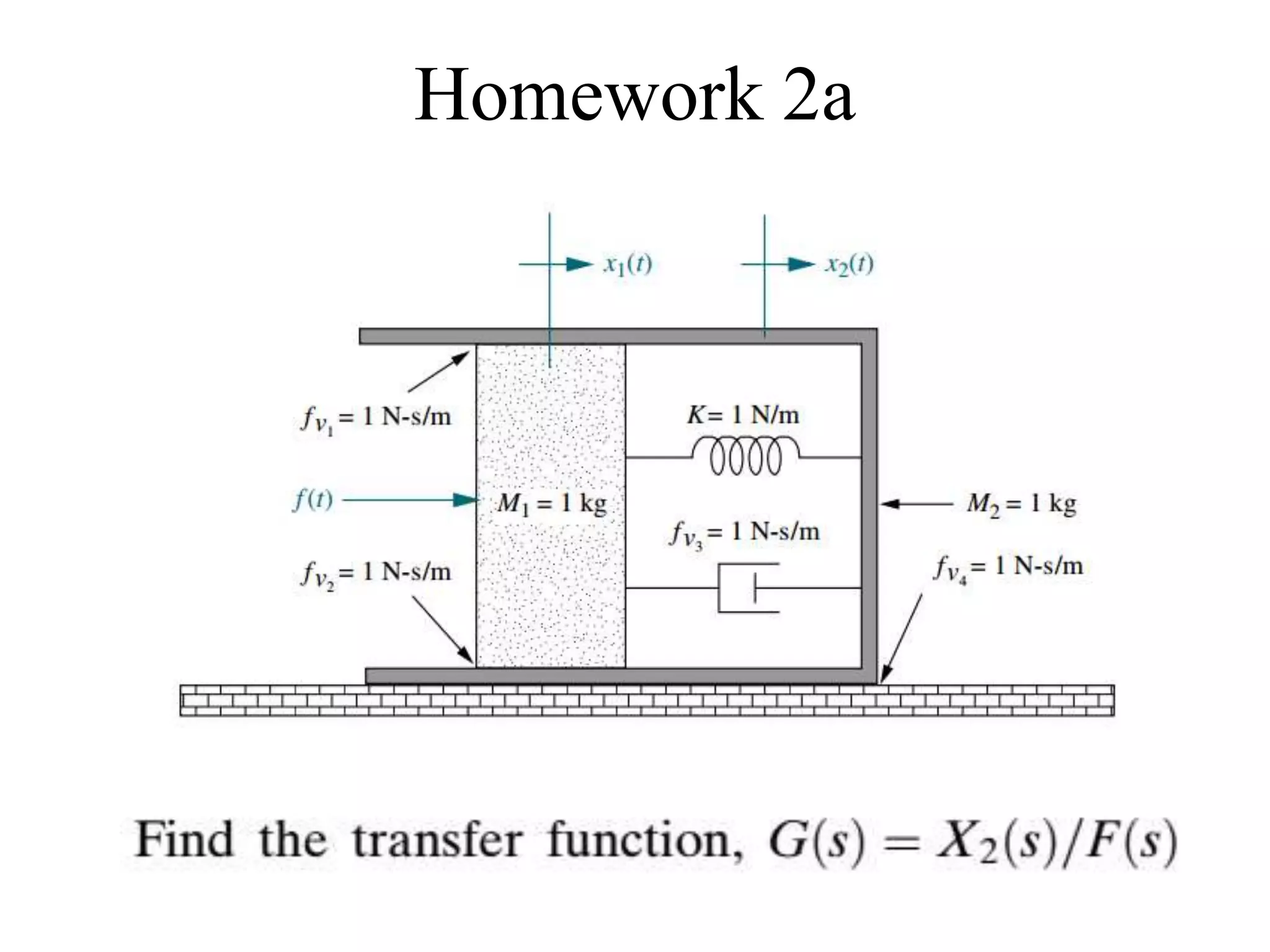
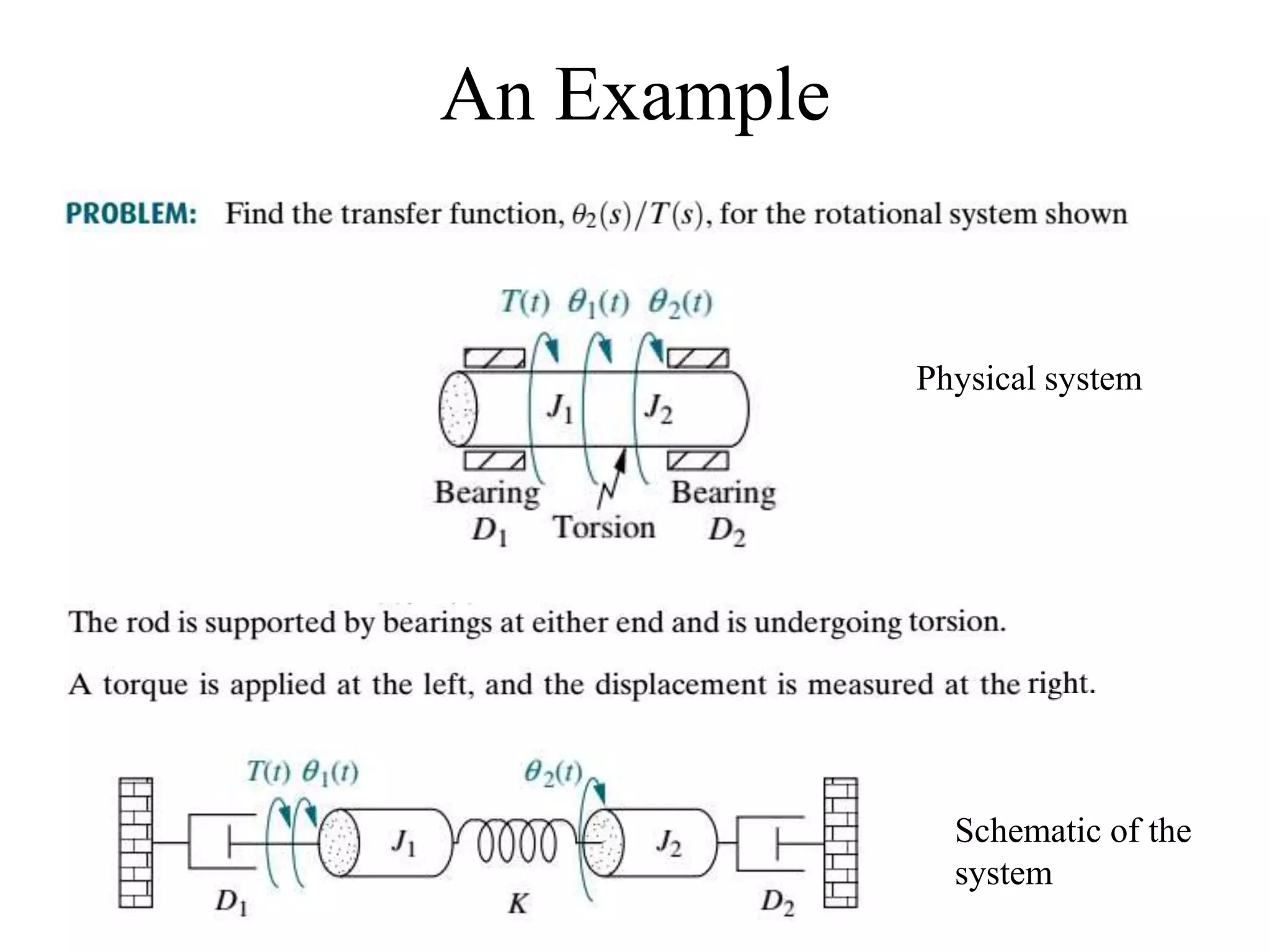
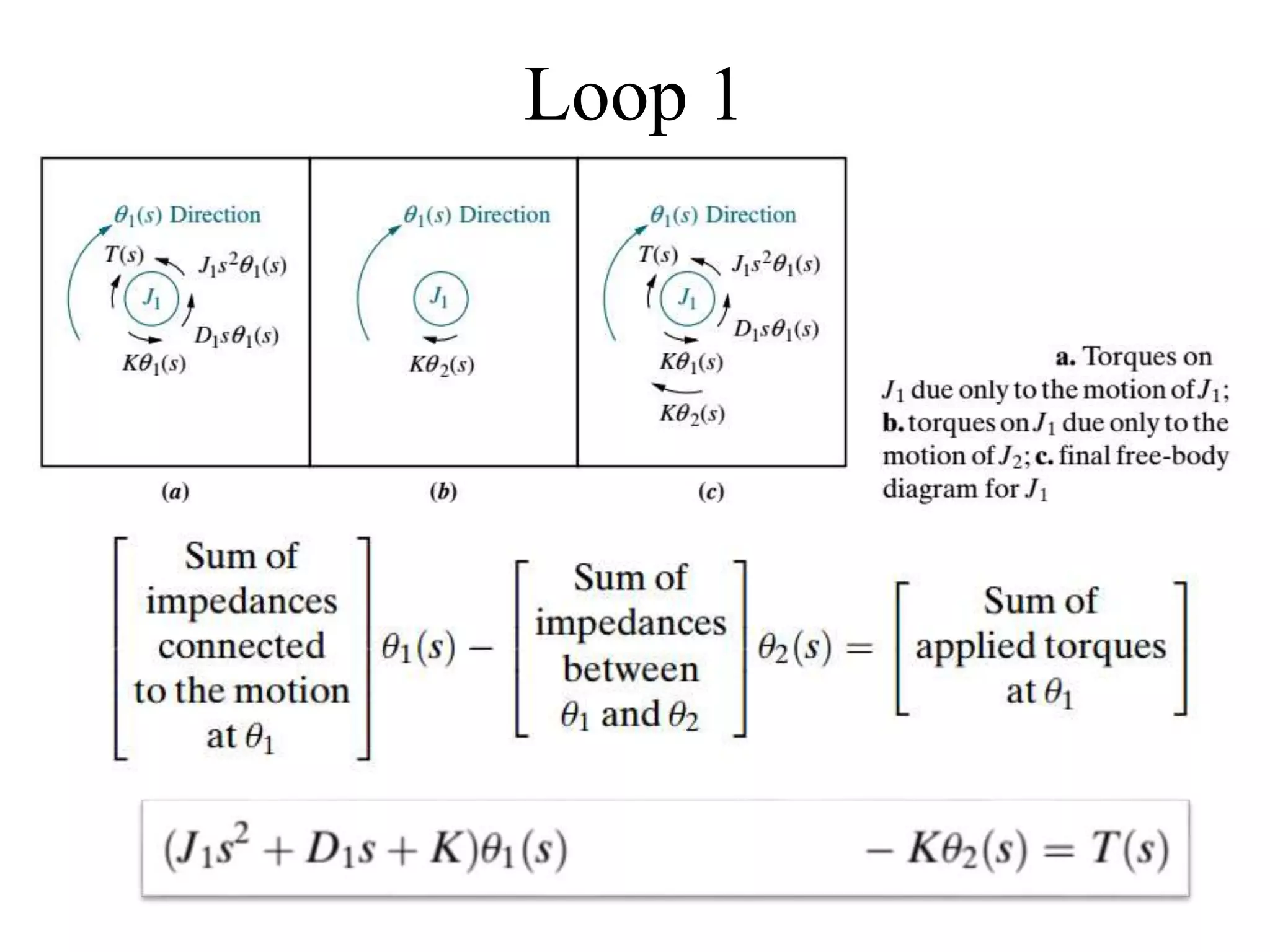
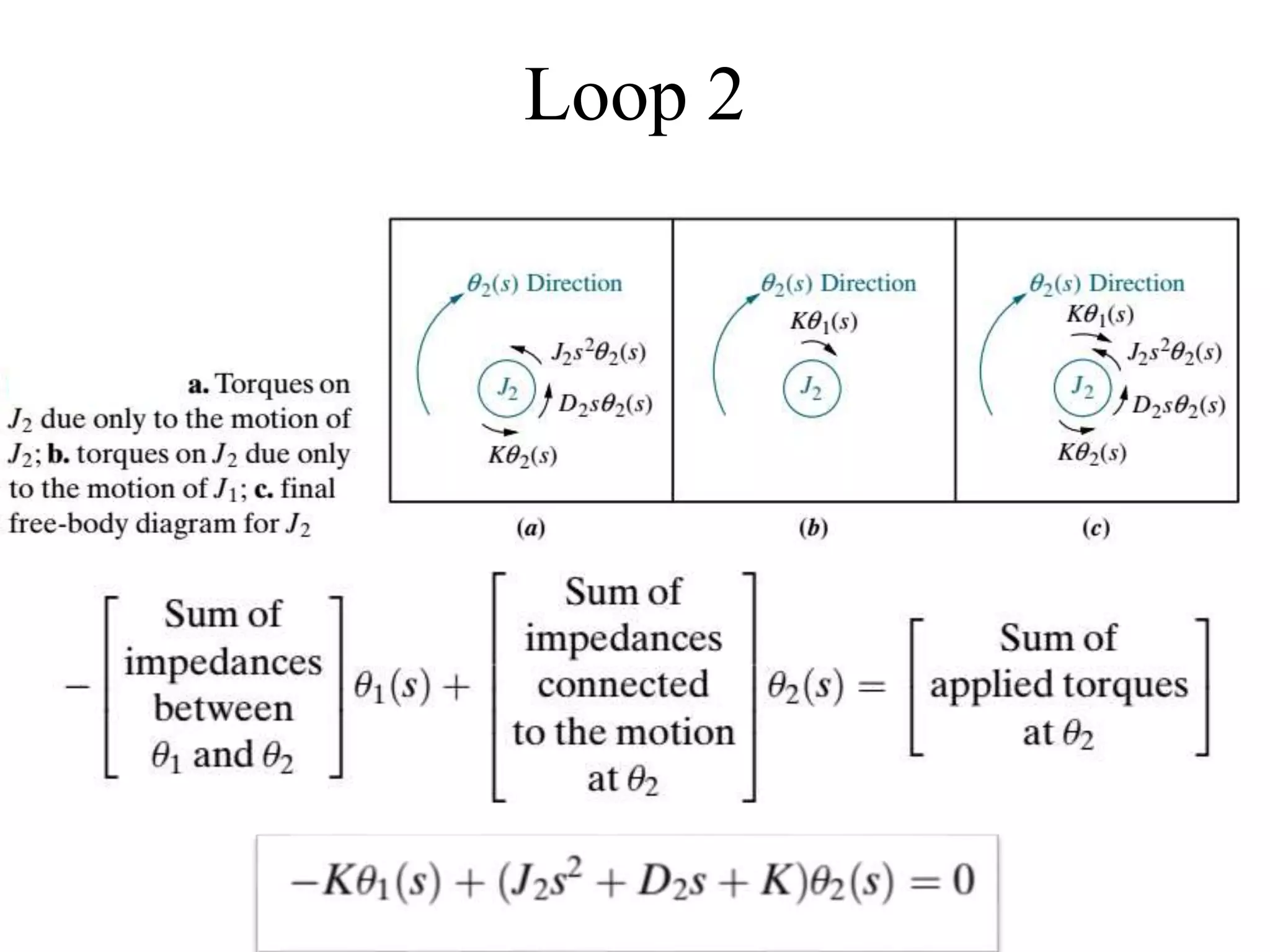
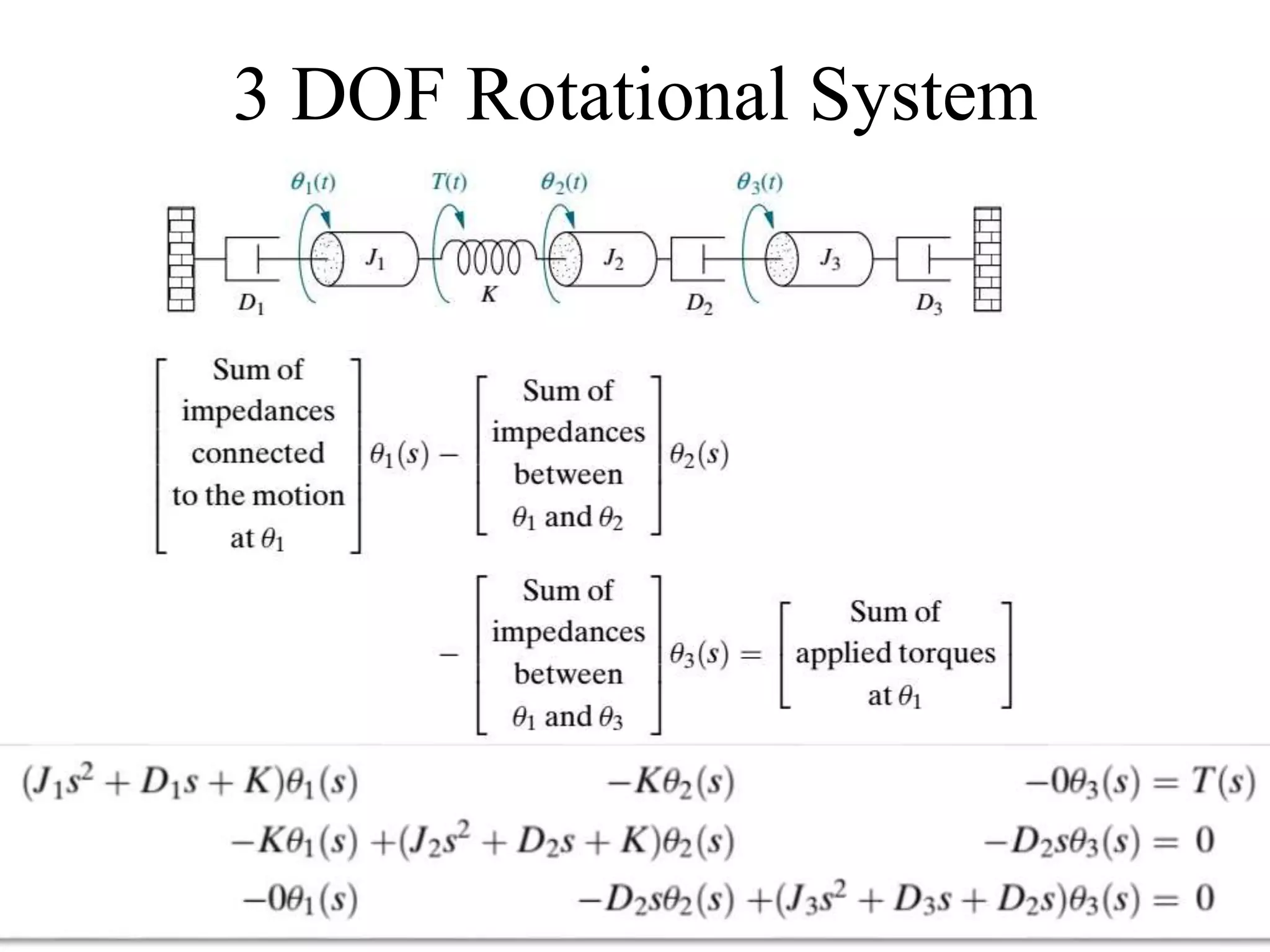
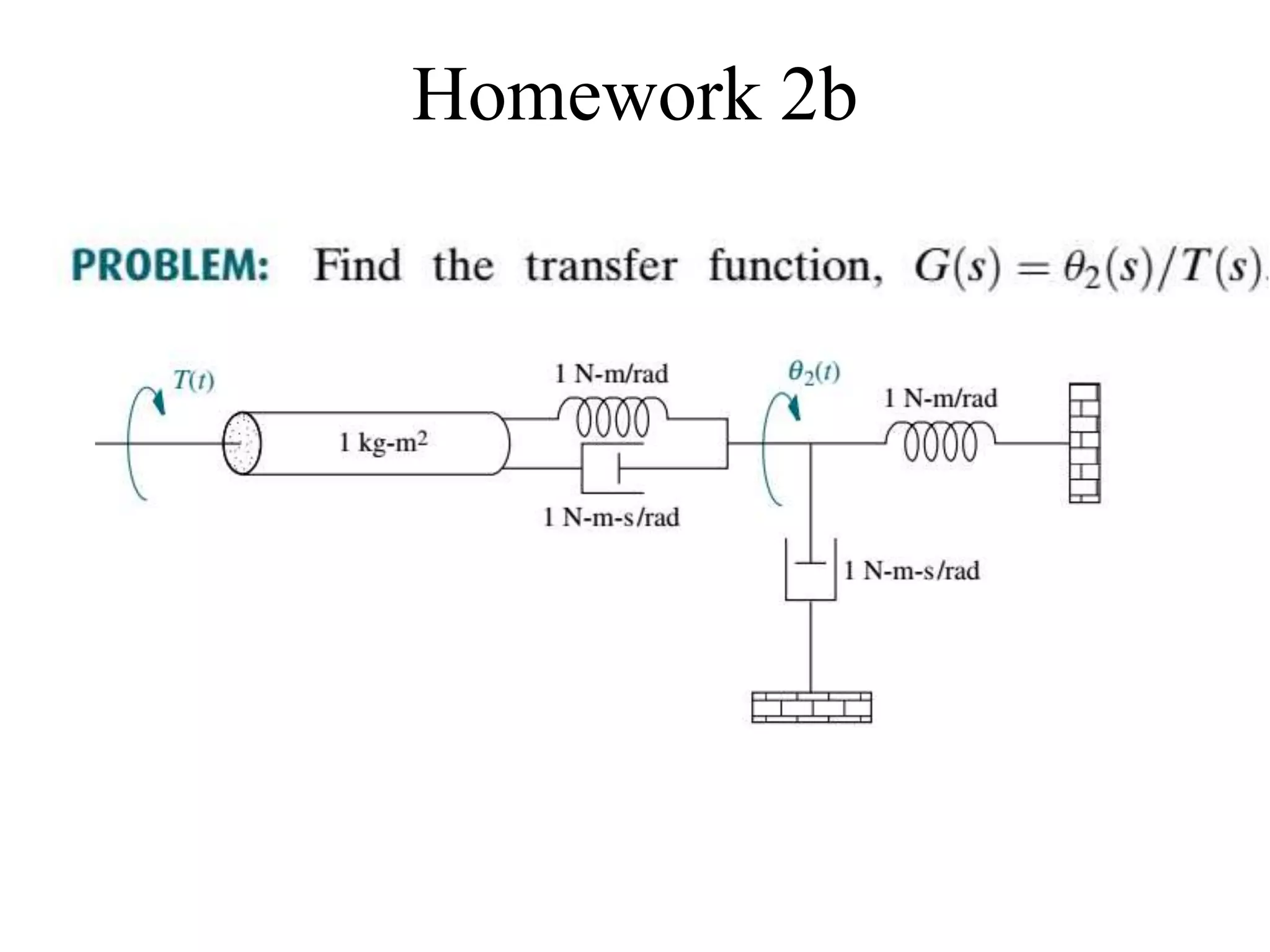
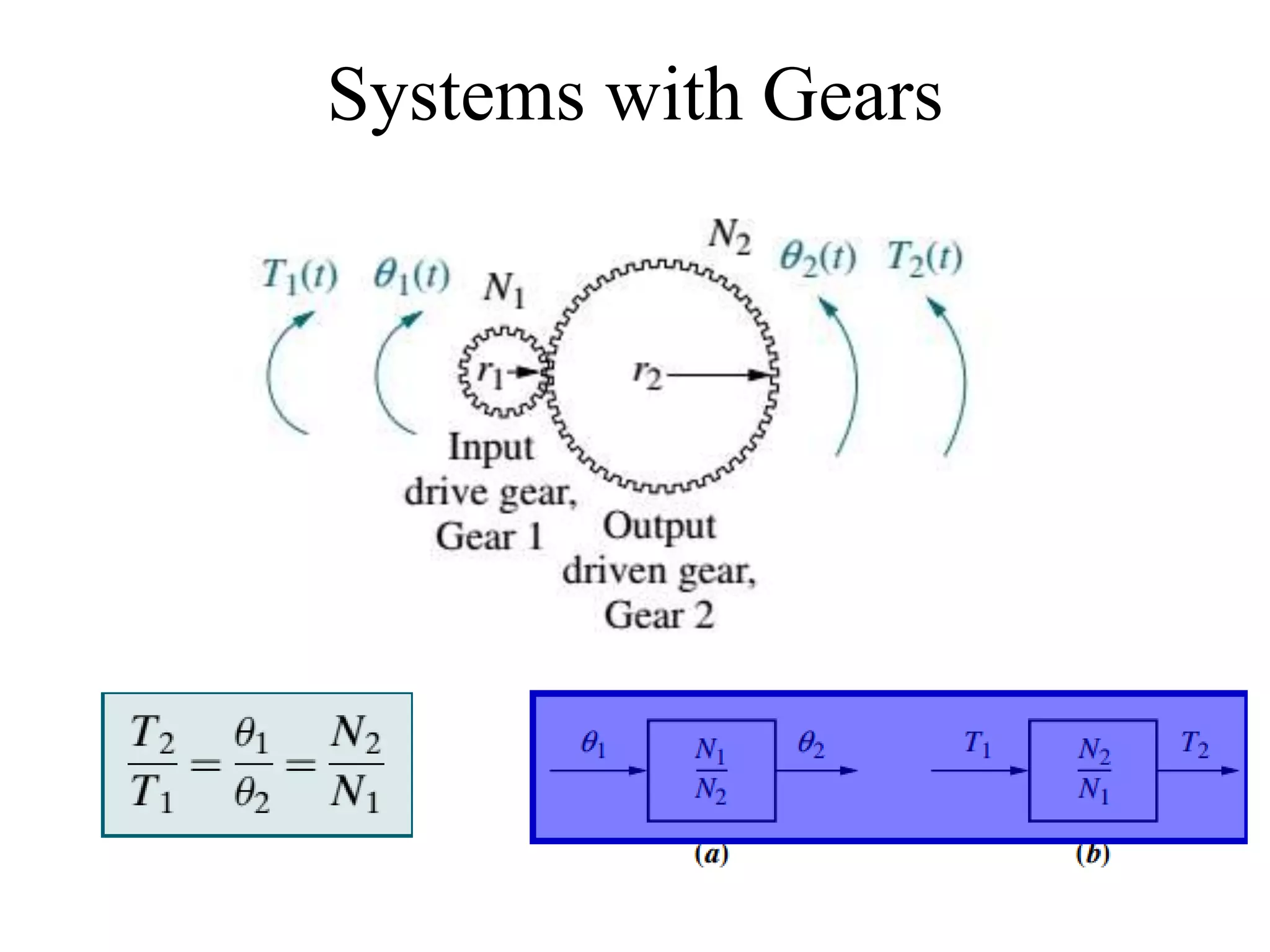
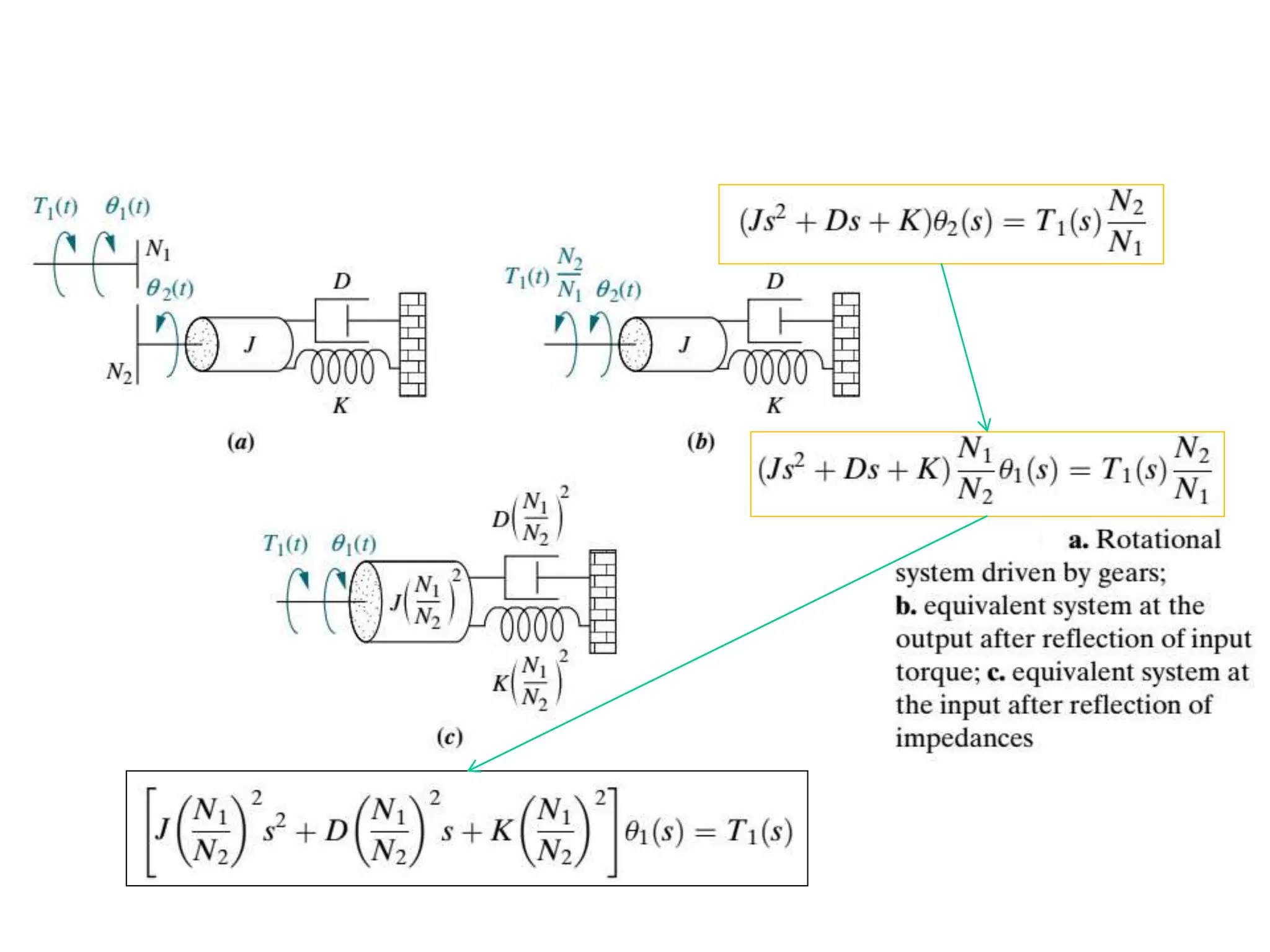
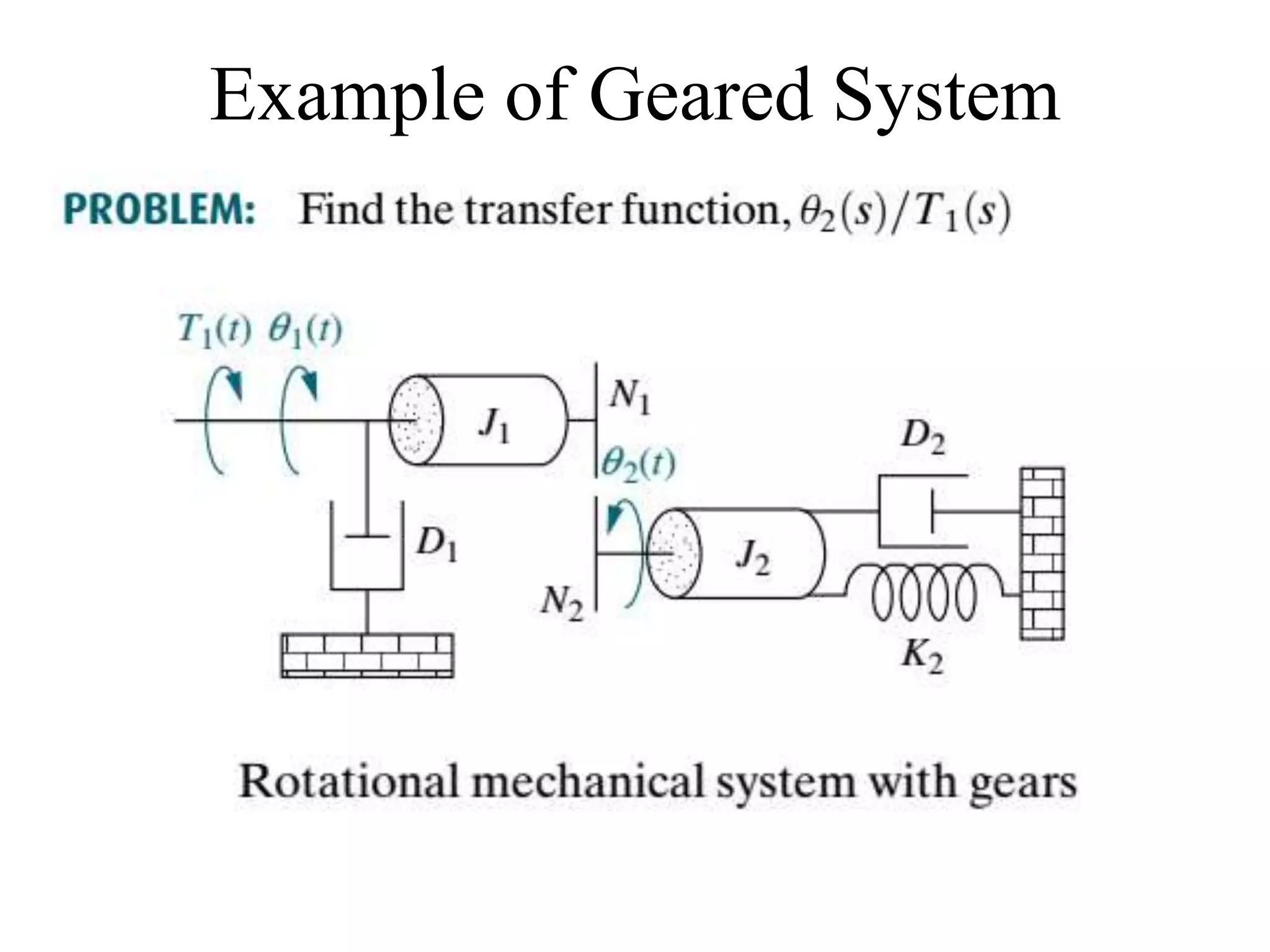
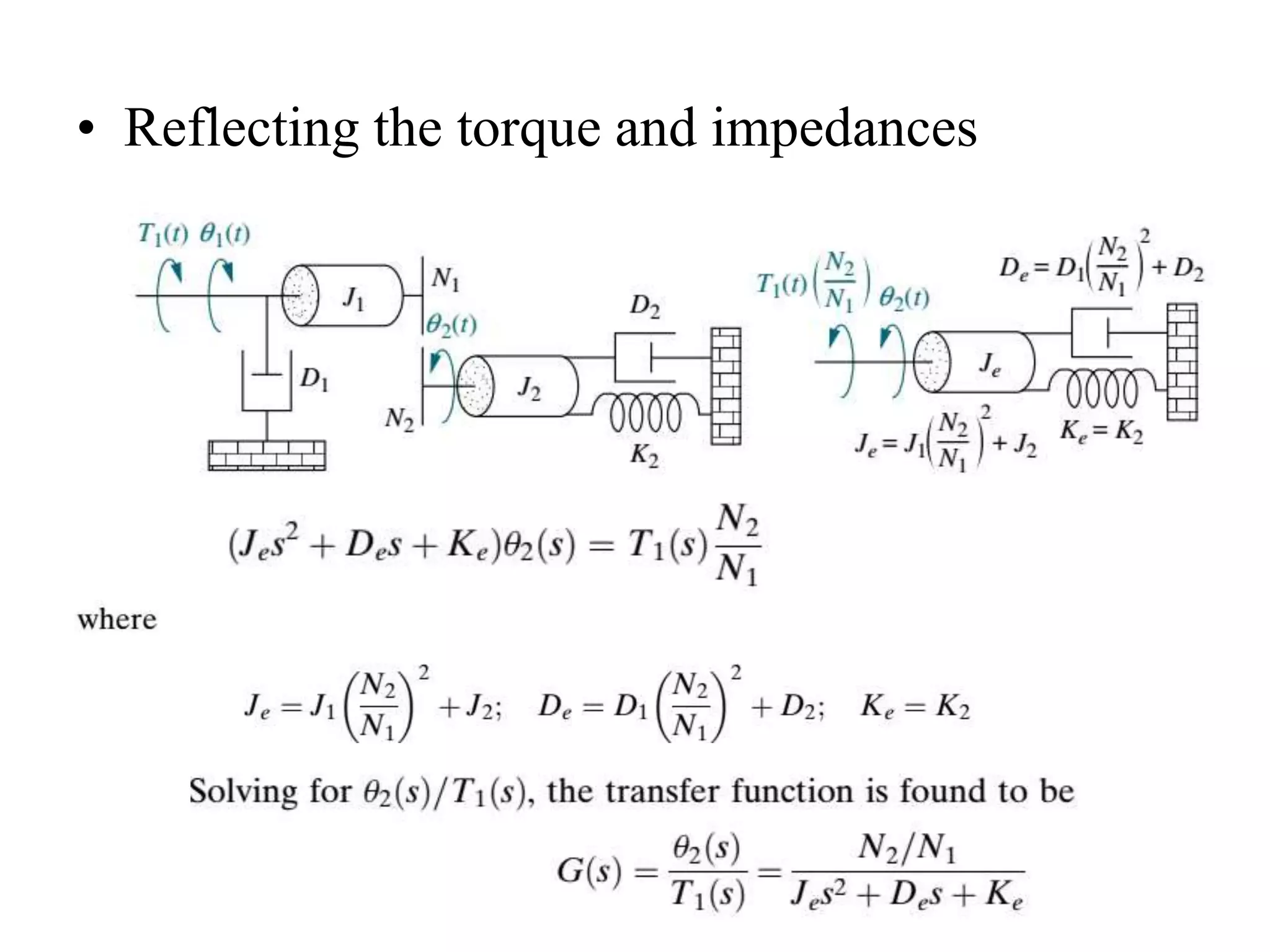
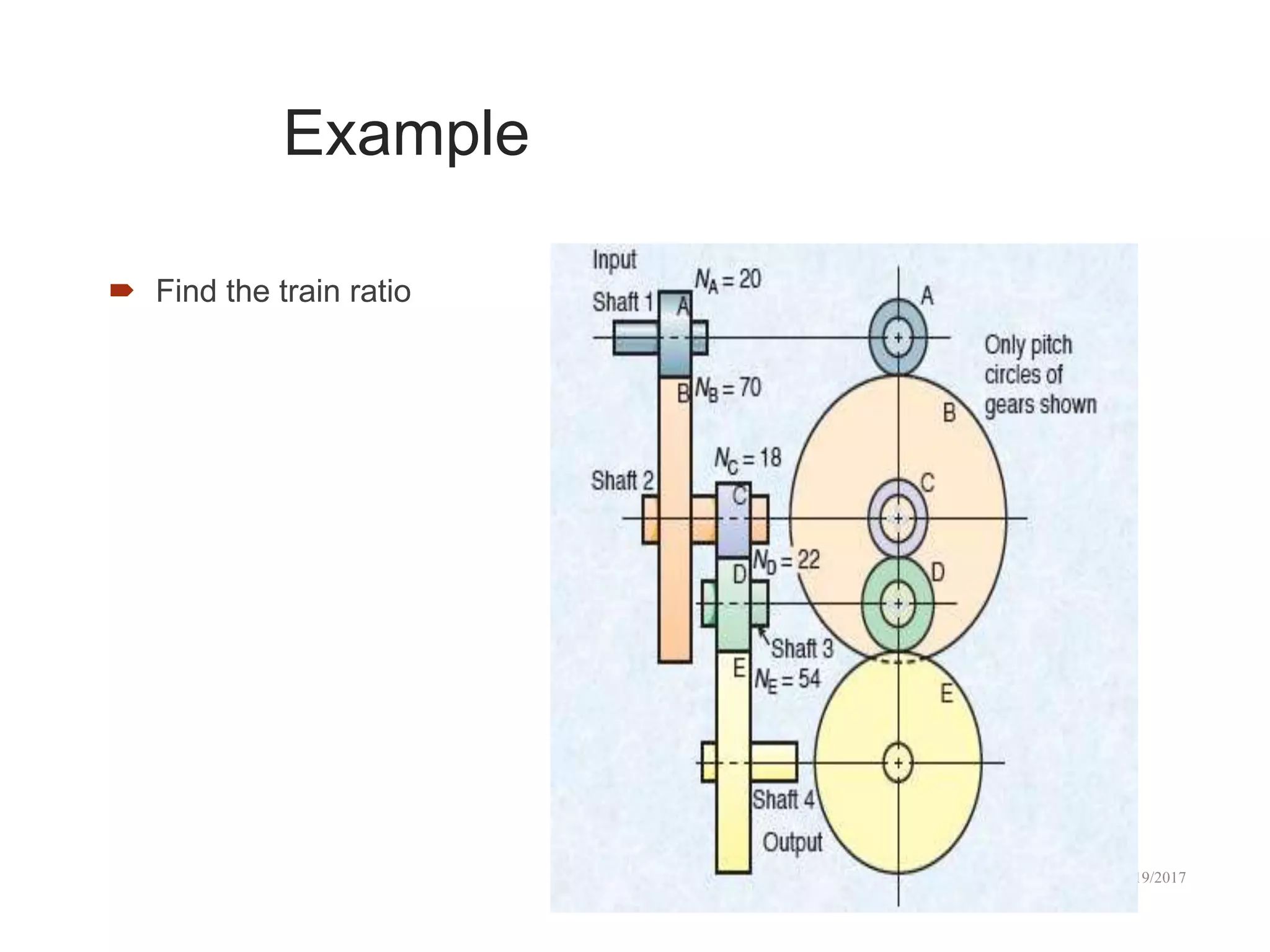
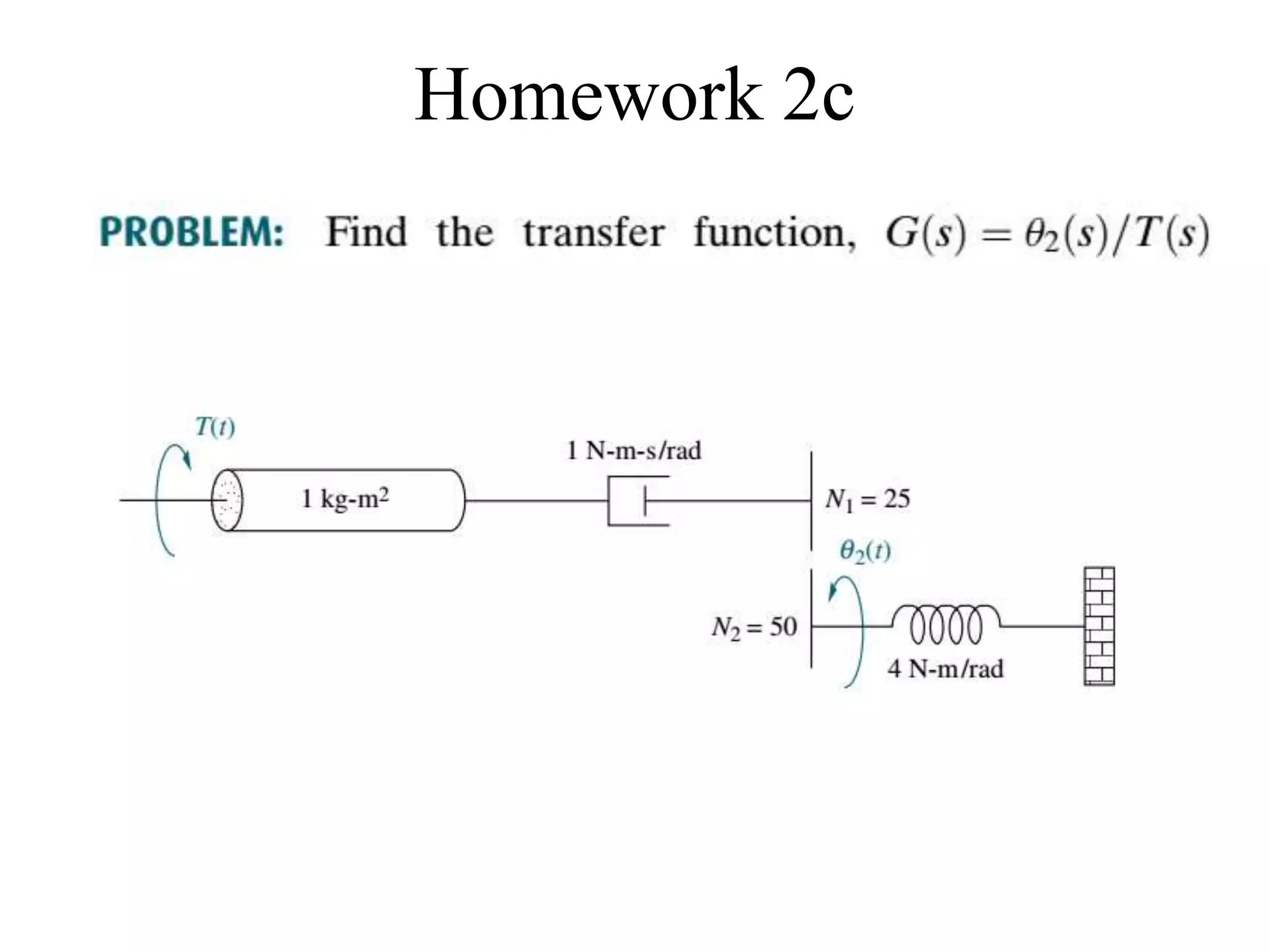
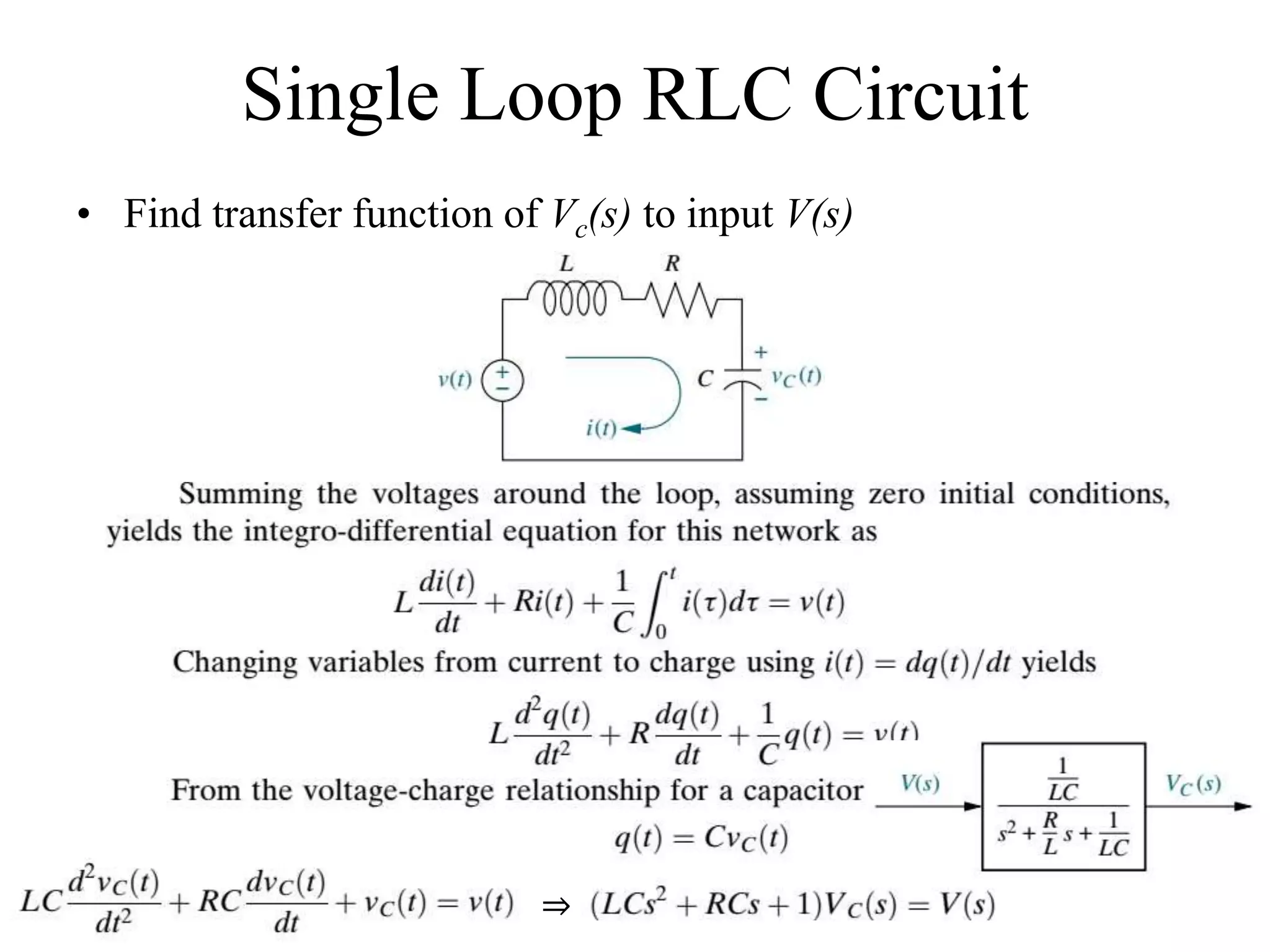
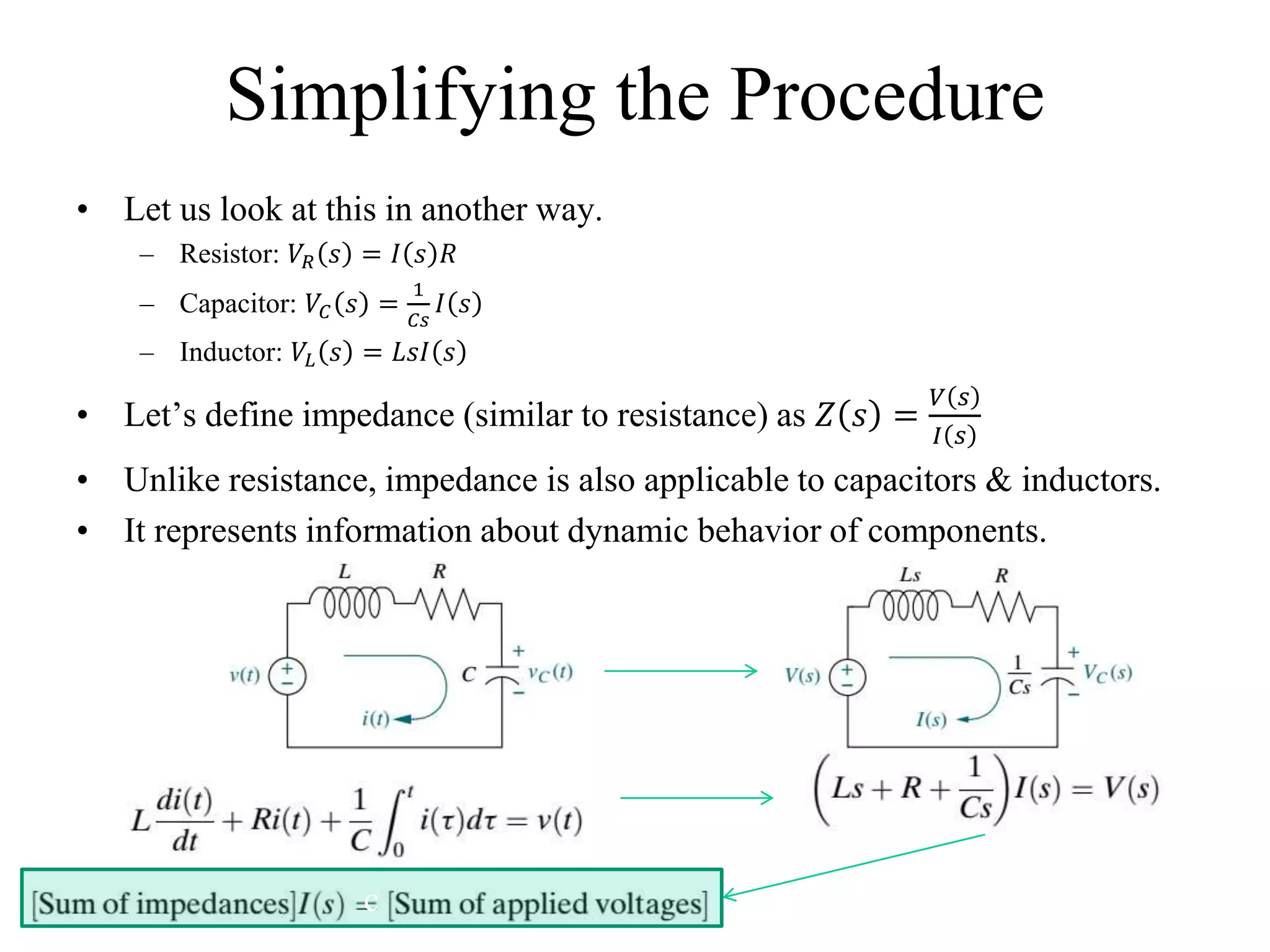
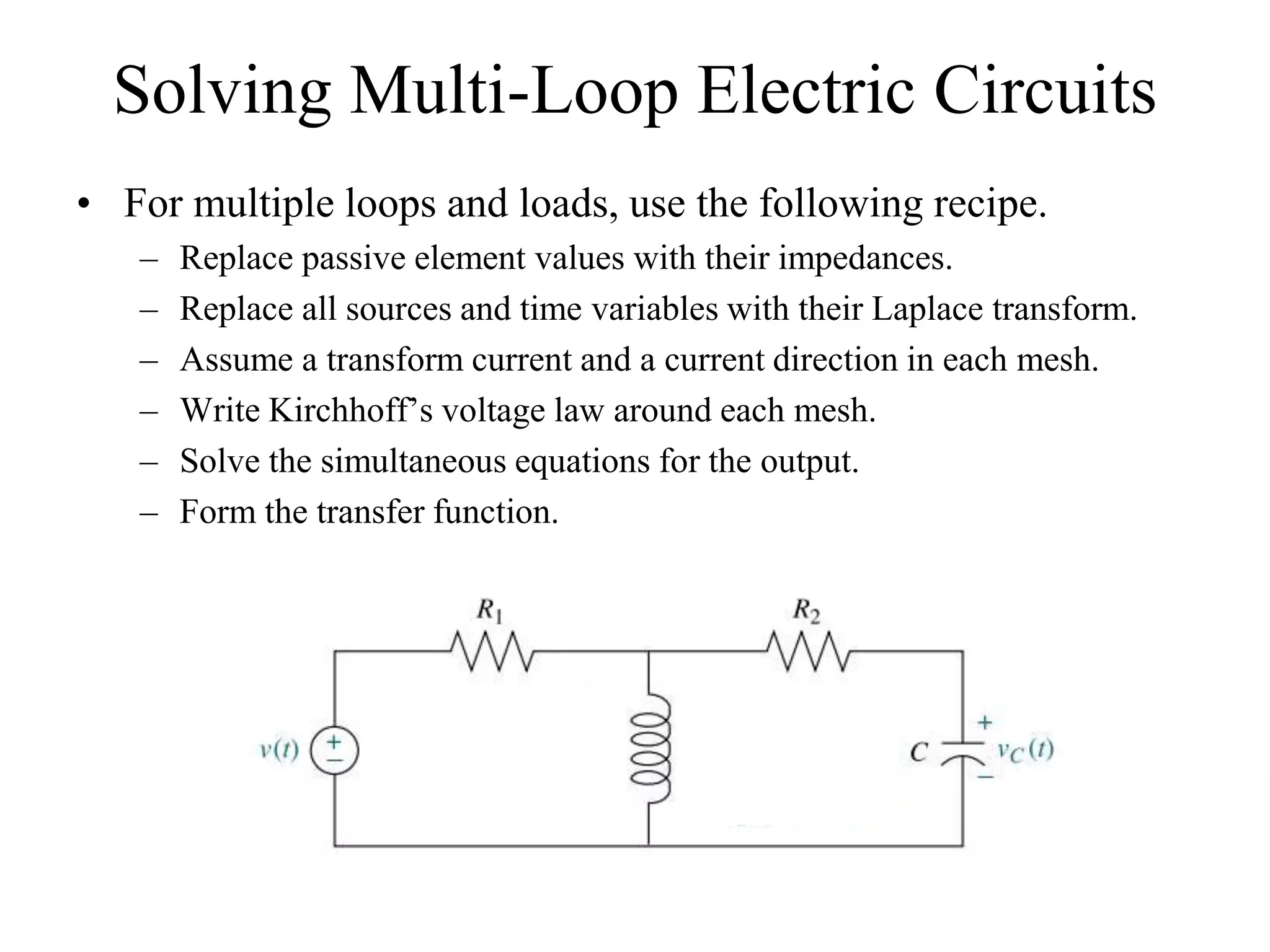
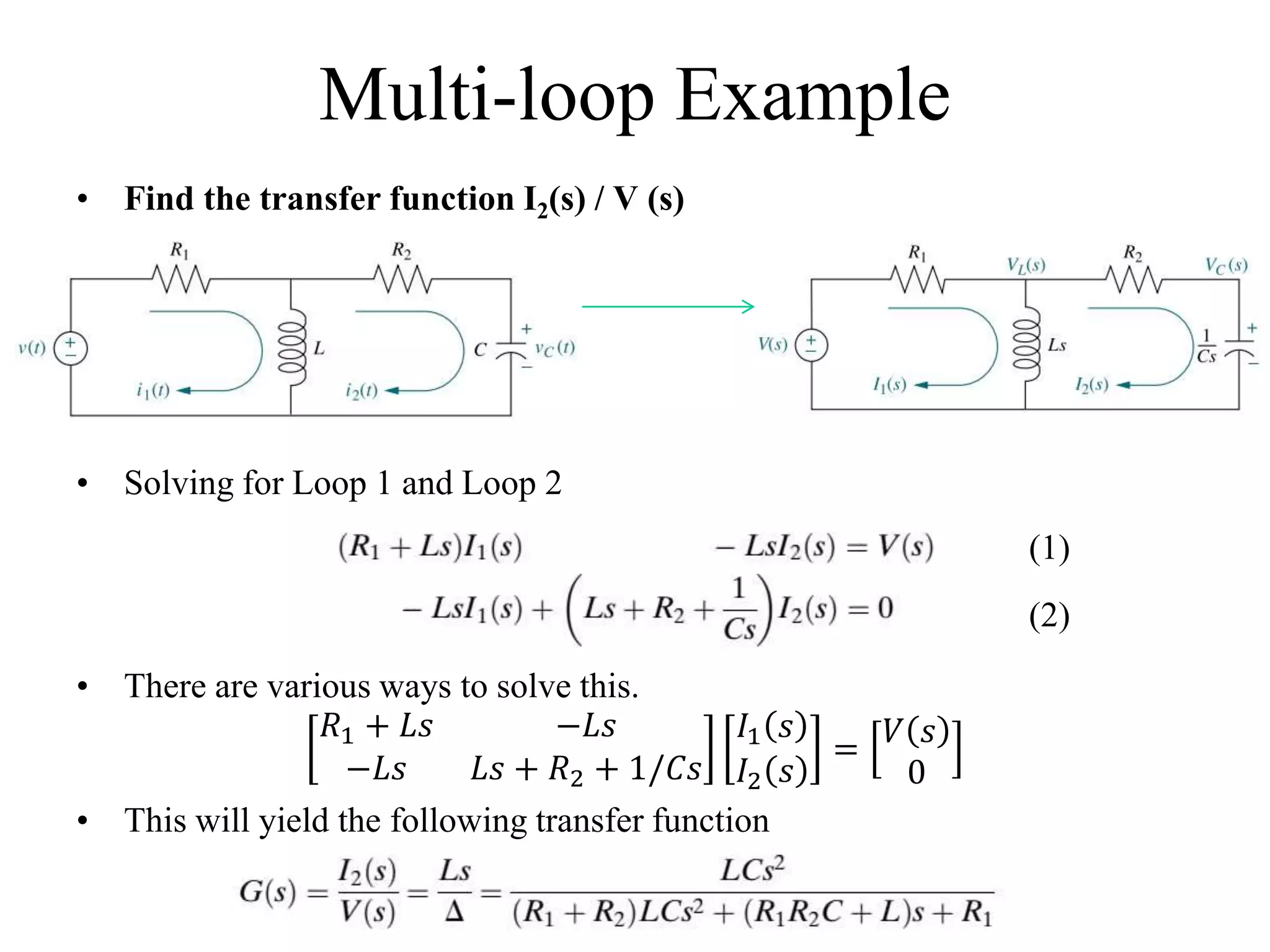
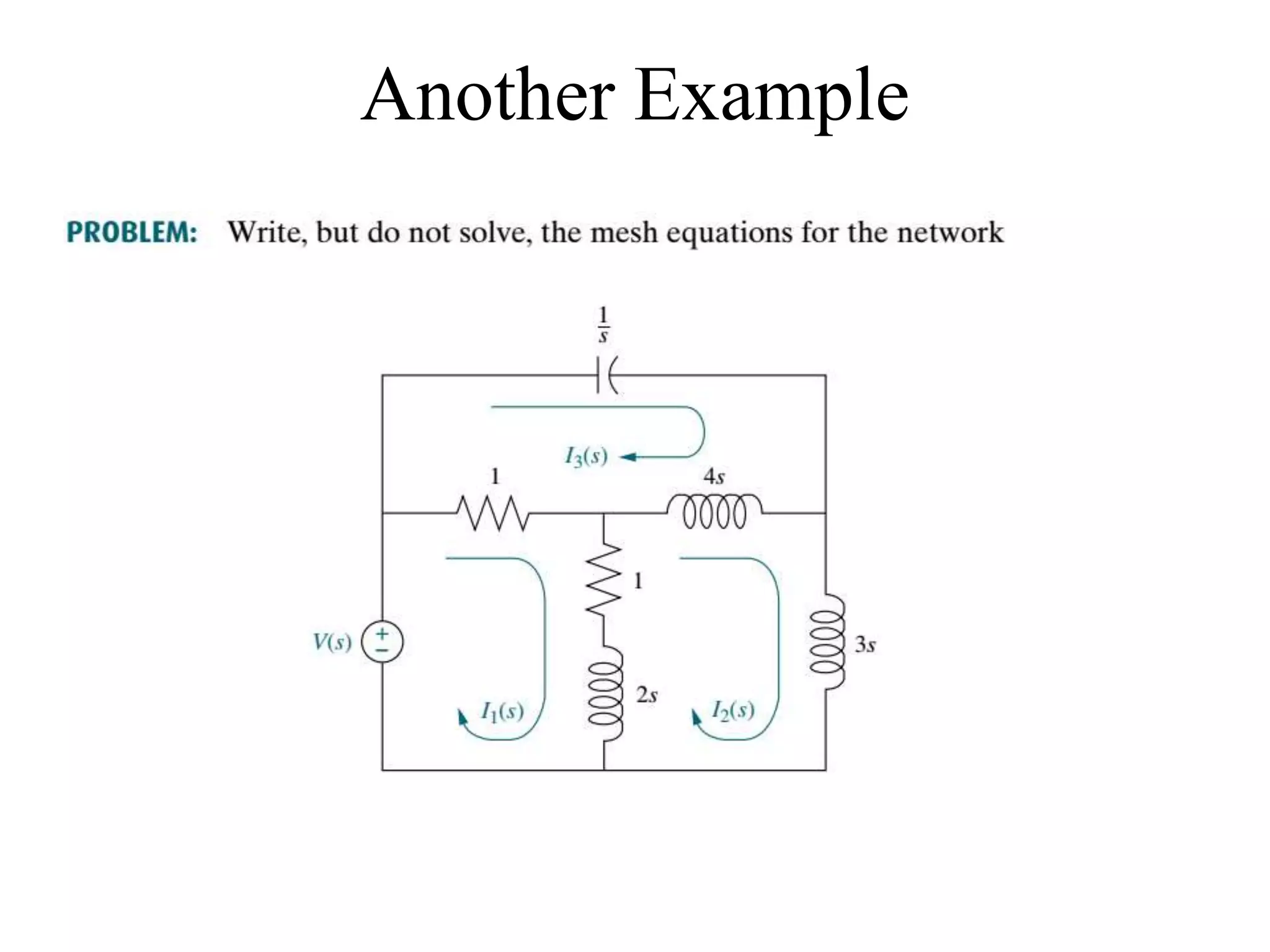
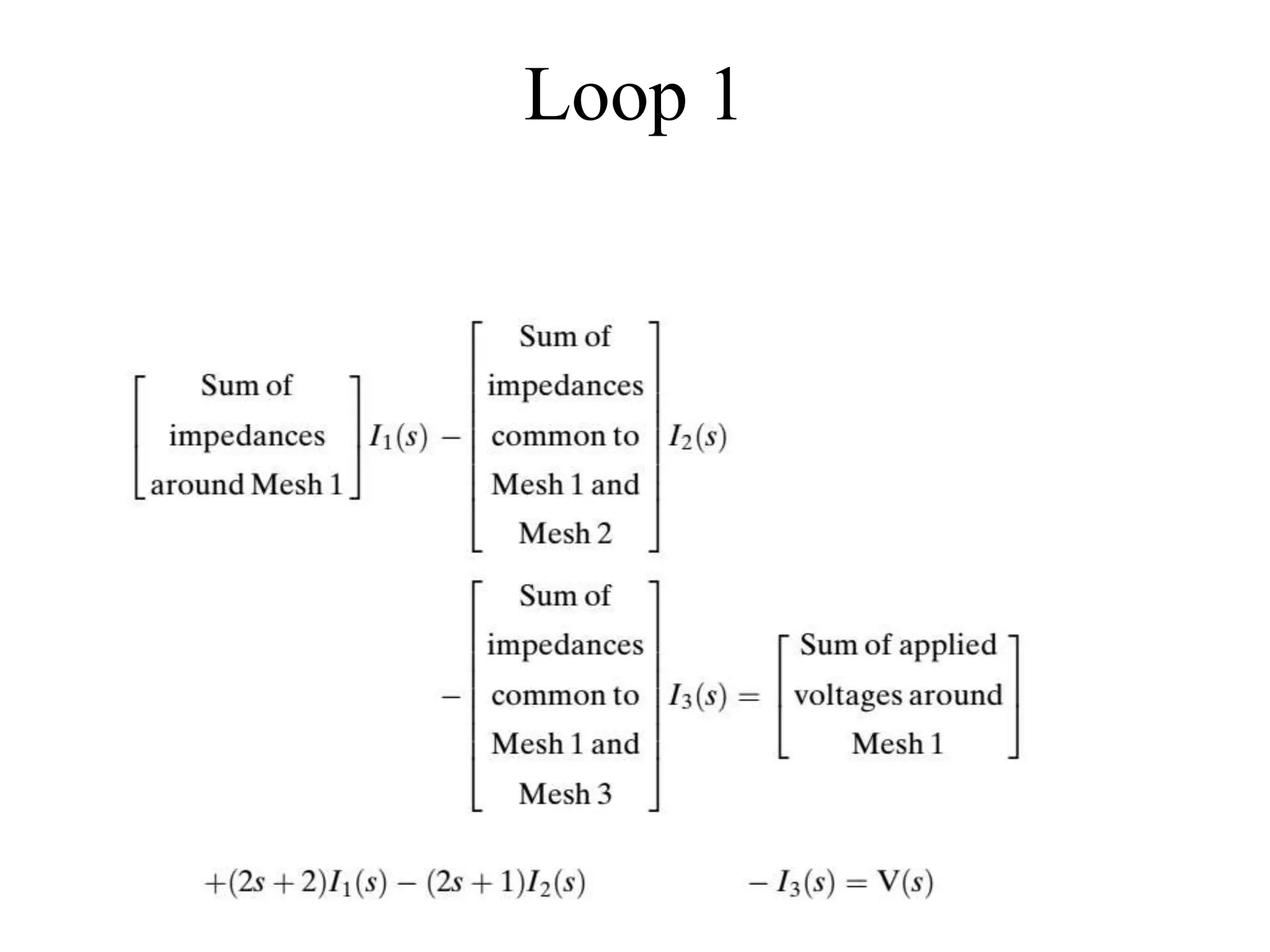
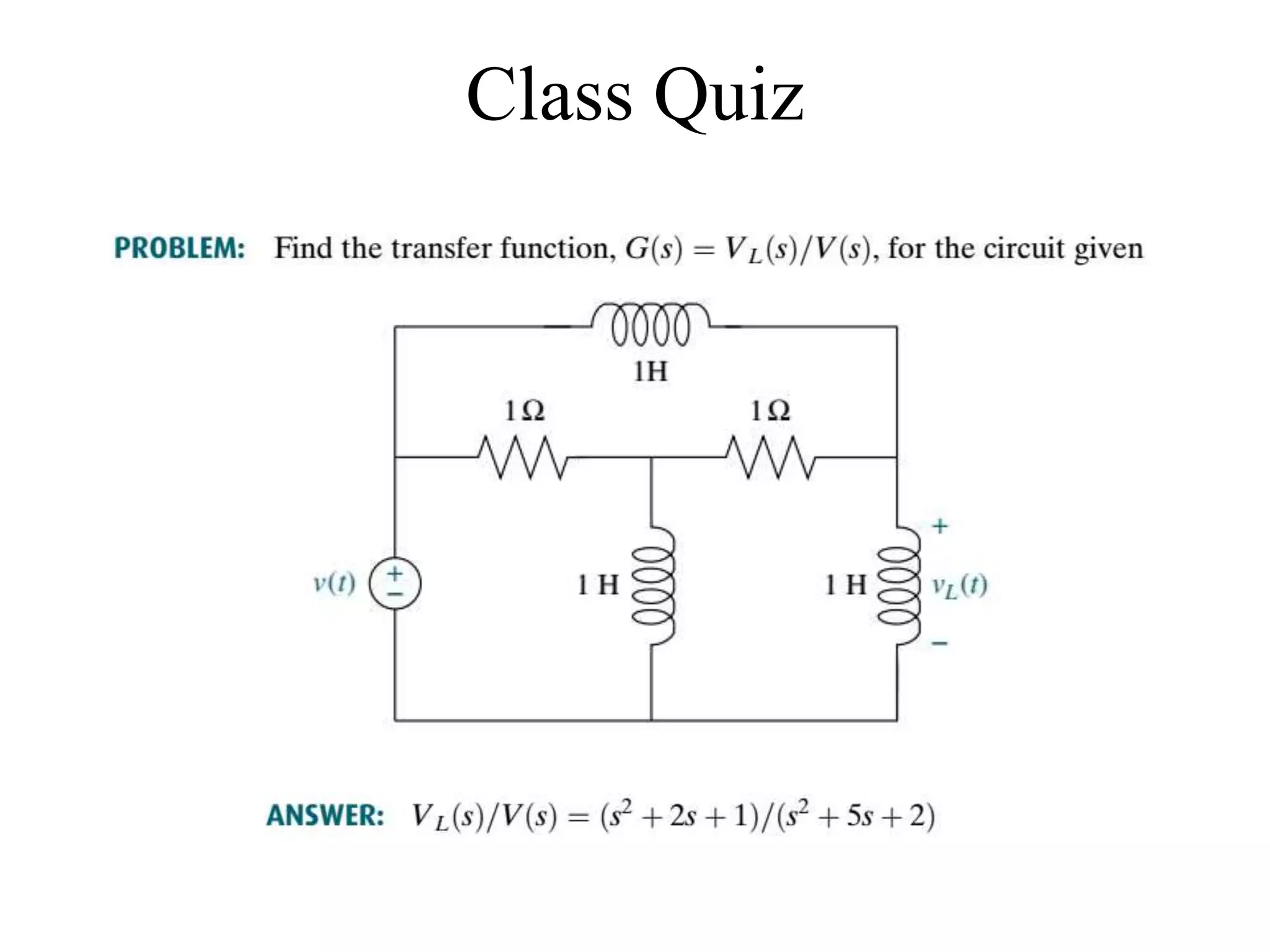
The document discusses the modeling of dynamical systems in control engineering, emphasizing the use of differential equations across various fields such as mechanical and electrical systems. It illustrates the similarities between electrical and mechanical components, including the translation of concepts like impedance and transfer functions. Additionally, it covers the complexities of multi-loop circuits and analogies in mechanical systems, stating that both can be analyzed using similar methods and equations.

1. ME-314 Control Engineering
Dr. Bilal A. Siddiqui
Mechanical Engineering
DHA Suffa University
and Brian Douglas

2. Mathematic Modeling of Dynamical
Systems
• Dynamics of many systems can be written in terms of differential equations
– Mechanical, thermal, electrical, economic, biological systems etc.
• We said that these D.E.’s can be derived using basic physical laws
• All systems we will study will be ‘causal’, i.e. the system’s response at any
time ‘t’ depends only on past and not future inputs
• We should always be aware about
– The scope of our assumptions (how valid they are and when are they valid?)
– Simplicity is desired but oversimplification is also dangerous
• Recall transfer functions:
– It is the ratio of Laplace Transform of output to Laplace Transform of input, when initial
conditions are zero.
– We assume
• Zero initial conditions
• Linearity
• Time Invariance

3. Similarities in Mechanical and
Electrical Systems
• 3 basic components
in mech systems:
– Mass
– Spring
– Damper
• 3 basic components
in electric systems:
– Resistance
– Capacitor
– Inductor
• Basic form of differential equations is the same.
• Therefore, learning to model one type of system easily leads to modeling
method for the other.
• Also, electrical and mechanical systems can be easily cascaded in block
diagrams due to this similarity.
• In fact, many other types of systems have similar forms
• We will begin with electrical systems. This will make modeling mech easier!

4. Modeling Electrical Systems (Nise)
• Current (i) is the rate of flow of charge (q)
𝑖 𝑡 =
𝑑𝑞 𝑡
𝑑𝑡
⇒ 𝑞 𝑡 = 𝑖 𝑡 𝑑𝑡
• Taking Laplace transform
𝐼 𝑠 = 𝑠𝑄 𝑠 ⇒ 𝑄 𝑠 =
1
𝑠
𝐼(𝑠)
• Impedance (complex resistance) is defined as
𝑧 =
v
i
⇒ Z s =
V s
I s
• It’s mathematical inverse is called admittance.

5. Passive Electric Components
• Resistor:
 𝑣 𝑡 = 𝑖 𝑡 𝑅 = 𝑅
𝑑𝑞 𝑡
𝑑𝑡
⇒ 𝑉 𝑠 = 𝐼 𝑠 𝑅
 𝑖 𝑡 =
𝑣 𝑡
𝑅
⇒ 𝐼 𝑠 =
𝑉 𝑠
𝑅
• Capacitor:
 𝑣 𝑡 =
1
𝐶
𝑞 𝑡 =
1
𝐶
𝑖 𝑡 𝑑𝑡 ⇒ 𝑉 𝑠 =
1
𝐶𝑠
𝐼 𝑠
 𝑖 𝑡 = 𝐶
𝑑𝑣 𝑡
𝑑𝑡
⇒ 𝐼 𝑠 = 𝐶𝑠𝑉(𝑠)
• Inductor:
 𝑣 𝑡 = 𝐿
𝑑𝑖 𝑡
𝑑𝑡
= 𝐿
𝑑2 𝑞 𝑡
𝑑𝑡2 ⇒ 𝑉 𝑠 = 𝐿𝑠𝐼 𝑠
 𝑖 𝑡 =
1
𝐿
𝑣 𝑡 𝑑𝑡 ⇒ 𝐼 𝑠 =
1
𝐿𝑠
𝑉 𝑠

6. Summary of Passive Components
• We will combine these elements in complex
networks using Kirchoff’s Laws
– Current and Voltages in a loop sum to zeros

7. Single Loop RLC Circuit
• Find transfer function of Vc(s) to input V(s)
⇒

8. Simplifying the Procedure
• Let us look at this in another way.
– Resistor: 𝑉𝑅 𝑠 = 𝐼 𝑠 𝑅
– Capacitor: 𝑉𝐶 𝑠 =
1
𝐶𝑠
𝐼 𝑠
– Inductor: 𝑉𝐿 𝑠 = 𝐿𝑠𝐼 𝑠
• Let’s define impedance (similar to resistance) as 𝑍 𝑠 =
𝑉 𝑠
𝐼 𝑠
• Unlike resistance, impedance is also applicable to capacitors & inductors.
• It represents information about dynamic behavior of components.
c

9. Solving Multi-Loop Electric Circuits
• For multiple loops and loads, use the following recipe.
– Replace passive element values with their impedances.
– Replace all sources and time variables with their Laplace transform.
– Assume a transform current and a current direction in each mesh.
– Write Kirchhoff’s voltage law around each mesh.
– Solve the simultaneous equations for the output.
– Form the transfer function.

10. Multi-loop Example
• Find the transfer function I2(s) / V (s)
• Solving for Loop 1 and Loop 2
• There are various ways to solve this.
𝑅1 + 𝐿𝑠 −𝐿𝑠
−𝐿𝑠 𝐿𝑠 + 𝑅2 + 1/𝐶𝑠
𝐼1 𝑠
𝐼2 𝑠
=
𝑉 𝑠
0
• This will yield the following transfer function
(1)
(2)

11. Summarizing the Method
• Let us look at the pattern in the last example
• This form will help us write such equations rapidly
• Mechanical equations of motion (covered next) have the same
form. So, this form is very useful!

12. Another Example

13. Loop 1

14. Loop 2
Loop 3

15. Solving Using Matlab
(1)
(2)
(3)

16. Class Quiz

17. Mechanical Systems (Translational)
• Many concepts applied to electrical networks can also be
applied to mechanical systems via analogies.
• This will also allow us to model hydraulic/pneumatic/thermal
systems.

18. Electrical/Mechanical Analogies
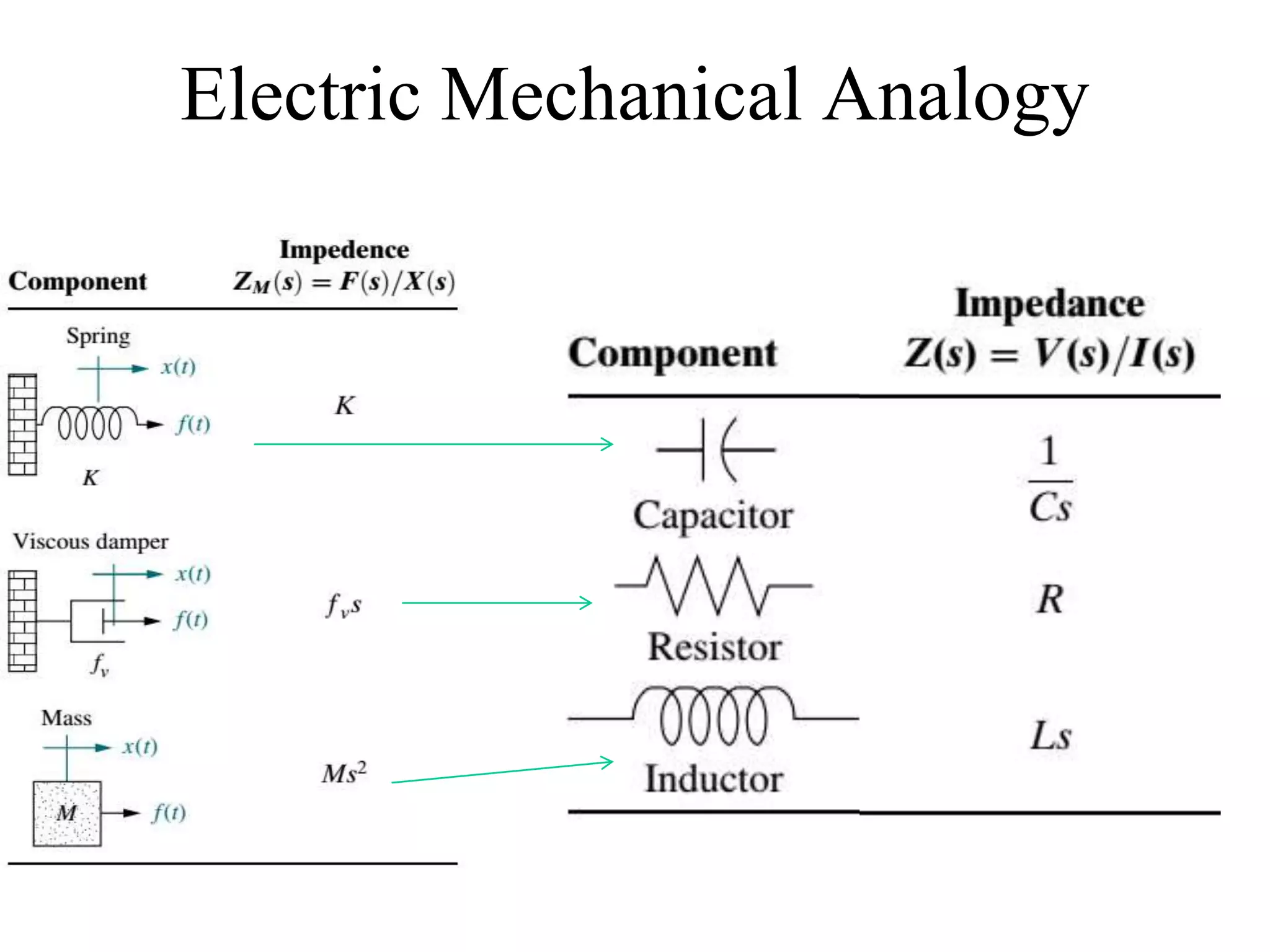
• Mechanical systems, like electrical networks, have 3 passive,
linear components:
– Two of them (spring and mass) are energy-storage elements; one of
them, the viscous damper, dissipates energy.
– The two energy-storage elements are analogous to the two electrical
energy-storage elements, the inductor and capacitor. The energy
dissipater is analogous to electrical resistance.
• Displacement ‘x’ is analogous to current I
• Force ‘f’ is analogous to voltage ‘v’
• Impedance (Z=V/I) is therefore Z=F/X
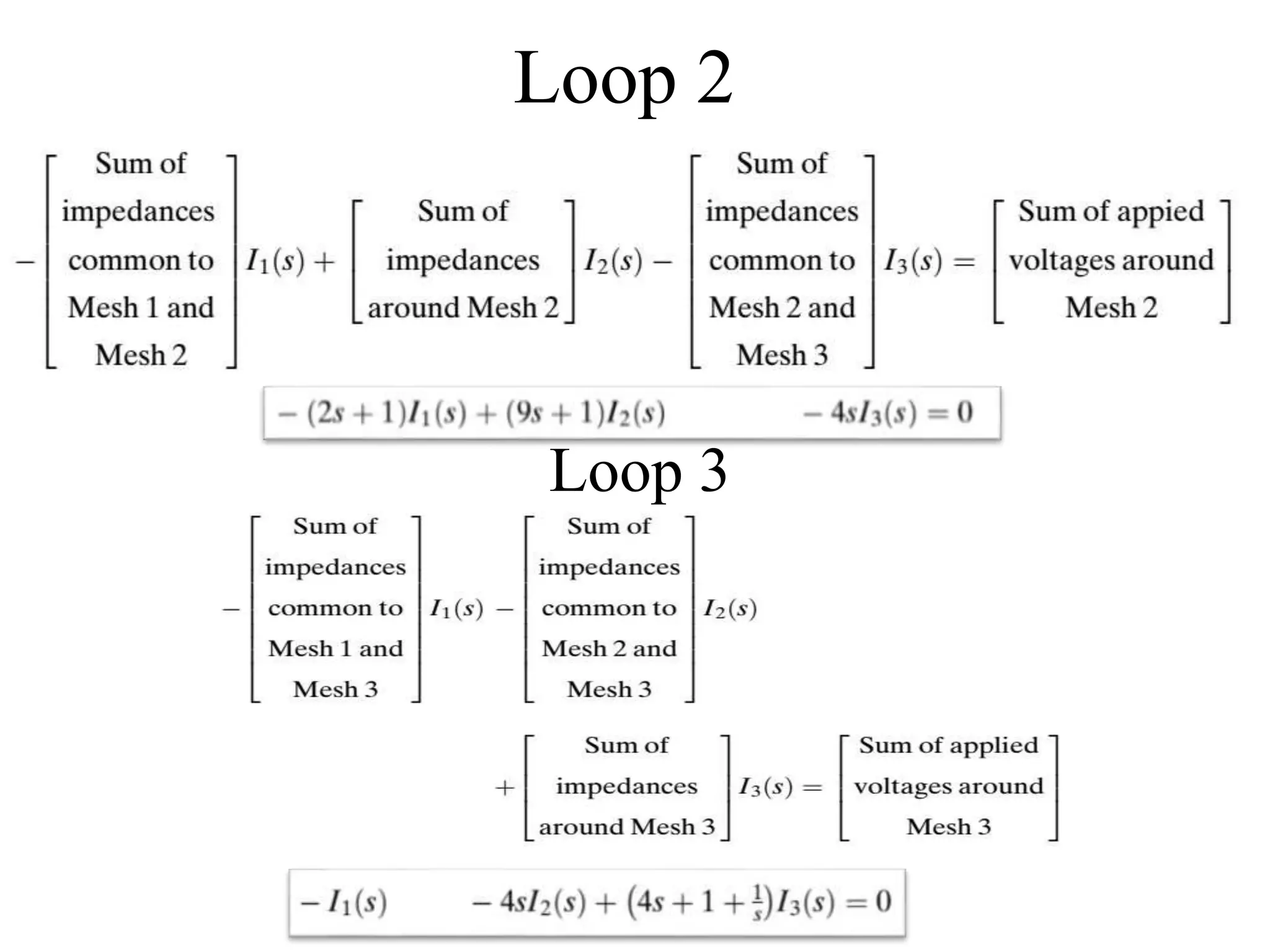
• Since, [Sum of Impedances] I(s) = [Sum of applied voltages]
• Hence, [Sum of Impedances] X(s) = [Sum of applied forces]

19. Electric Mechanical Analogy

20. Recall Spring Mass Damper System

21. Multiple Degrees of Freedom
Mechanical Systems
• Many mechanical systems are similar to multiple-loop and multiple-node
electrical networks, where more than one simultaneous differential equation is
required to describe the system.
• In mechanical systems, the number of equations of
motion required is equal to the number of linearly independent motions.
• Linear independence implies that a point of motion in a system can still move if
all other points of motion are held still.
• Another name for the number of linearly independent motions is the number of
degrees of freedom.
• In a two-loop electrical network, each loop current depends on the other loop
current, but if we open-circuit just one of the loops, the other current can still
exist if there is a voltage source in that loop.
• Similarly, in a mechanical system with two degrees of freedom, one point of
motion can be held still while the other point of
motion moves under the influence of an applied force.

22. 2 DOF Transfer Function
• System has two degrees of freedom, since each mass can be moved
in the horizontal direction while the other is held still.
• 2 simultaneous equations of motion will be required to describe system.
• The two equations come from free-body diagrams of each mass.
• Forces on M1 are due to (a) its own motion and (b) motion of M2 transmitted
to M1 through the system.

23. Force Analysis
a. Hold M2
still, move
M1 to right
b. Hold M1
still, move
M2 to right
c. combined
a. Hold M1
still, move
M2 to right
b. Hold M2
still, move
M1 to right
c. combined
Forces on M1 Forces on M2

24. Use Analogy
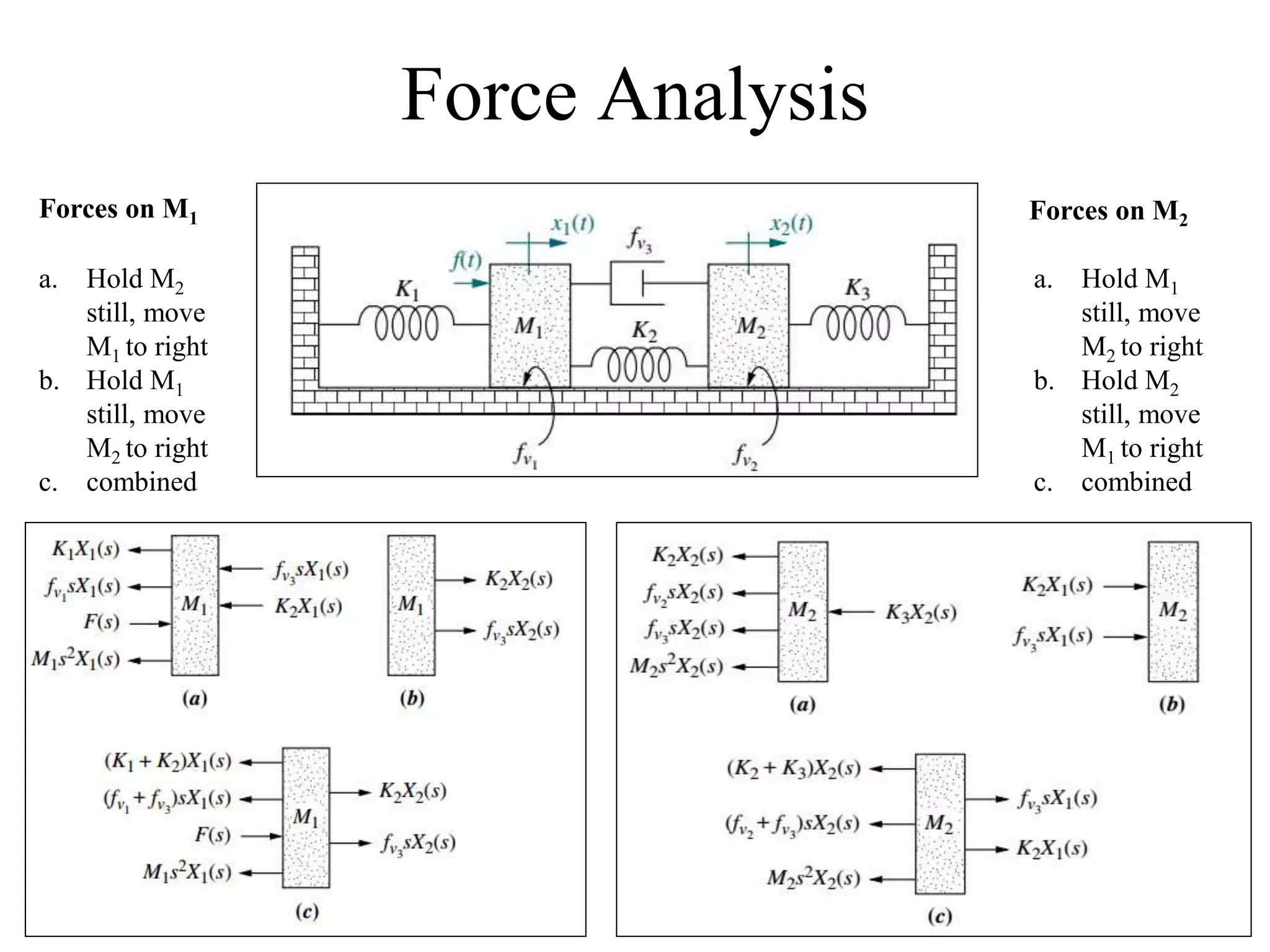
[(𝑀1 𝑠2 + 𝑓𝑣1
+ 𝑓𝑣3
𝑠 + (𝐾1+𝐾2)] 𝑋1 𝑠 − (𝐾2+𝑓𝑣3
𝑠)𝑋2 𝑠 = 𝐹 𝑠
−(𝐾2+𝑓𝑣3
𝑠)𝑋1 𝑠 + [(𝑀2 𝑠2
+ 𝑓𝑣2
+ 𝑓𝑣3
𝑠 + (𝐾1+𝐾2)]𝑋2 𝑠 = 0
Loop 1
Loop 2

25. 3 DOF Translational System

26. Loop 1

27. Loop 2

28. Loop 3

29. Homework 2a

30. Mechanical Systems (Rotational)
• Torque replaces force ; angular displacement replaces
translational displacement.

31. An Example
Physical system
Schematic of the
system

32. Loop 1

33. Loop 2

34. 3 DOF Rotational System

35. Homework 2b

36. Systems with Gears

38. Generalizing for Gears
• From the following observation

39. Example of Geared System

40. An important note
• Intuitively, we will start forming two
simultaneous equations for each inertia.
• But, the inertias are not independent (we
cannot stop the motion of one and study the
motion of the other), since they are tied
together by the gears.
• Thus, there is only one degree of freedom and
hence one equation of motion !

41. • Reflecting the torque and impedances

42. Gear Train
10/2/2017Spring 312 ( Cpoyrights Bilal Siddiqui 2015
42
• Max gear ratio of only about 10 : 1 can be obtained with one pair of gears.
• Greater ratios can be obtained in less space and with fewer dynamic
problems by compounding additional pairs of gears.
• A two-stage compound gear train can obtain a train value of up to 100 : 1.
• Consider a pinion 2 driving a gear 3. The speed of the driven gear is
𝑛3 =
𝑁2
𝑁3
𝑛2 =
𝑑2
𝑑3
𝑛2
• This relation is valid regardless of the type of gears meshed.
• Consider the more complex train shown above.
• The train ratio is simply 𝑛6 = −
𝑁2
𝑁3
𝑁3
𝑁4
𝑁5
𝑁6
𝑛2
• In other words, 𝑛 𝐿 = 𝑒. 𝑛 𝐹
• Where, 𝑒 =
𝑝𝑟𝑜𝑑𝑢𝑐𝑡 𝑜𝑓 𝑑𝑟𝑖𝑣𝑖𝑛𝑔 𝑡𝑜𝑜𝑡ℎ 𝑛𝑢𝑚𝑏𝑒𝑟𝑠
𝑝𝑟𝑜𝑑𝑢𝑐𝑡 𝑜𝑓 𝑑𝑟𝑖𝑣𝑒𝑛 𝑡𝑜𝑜𝑡ℎ 𝑛𝑢𝑚𝑏𝑒𝑟𝑠
• nL is the speed of the last gear and nF is the speed of the first gear in the
train.

43. More on Gear Trains
• Making a train also helps reduce the package size
• Sometimes, idler gears are necessary to provide support to
one of the gears.
• Used in many applications, like automobiles, rotorcraft etc
10/2/2017
43

44. Example
 Find the train ratio
10/2/2017
44

45. Gear Trains

46. Example with Gear Train

47. Gear Train System (continued)
• Therefore, the transfer function will be

48. Homework 2c

49. Modeling Electromechanical Systems
• Systems that are hybrid of electrical and mechanical systems

50. DC Motor – An Electromechanial System
• Mechanical output (θ), electrical input (V)

51. Schematic of DC Motor

52. How DC Motor works?
• A rotating circuit called the armature, through which current ia
flows, passes through the fixed magnetic field at right angles and
feels a torque which turns the rotor. This torque is
𝑻 𝒎 𝒔 = 𝑲 𝒕 𝑰 𝒂 𝒔 ⇒ 𝑰 𝒂 𝒔 = 𝑻 𝒎 𝒔 /𝑲 𝒕
• When a conductor moves through a magnetic field, it develops a
voltage, called back emf eb, proportional to the speed.
𝒗 𝒃 𝒕 = 𝑲 𝒃
𝒅𝜽 𝒎
𝒅𝒕
⇒ 𝑽 𝒃 𝒔 = 𝑲 𝒃 𝒔𝜽 𝒎 𝒔
• Write the loop equation for the electric circuit
𝑬 𝒂 𝒔 = 𝑹 𝒂 + 𝑳 𝒂 𝒔 𝑰 𝒂 + 𝑽 𝒃 𝒔
• We can write
𝑬 𝒂 𝒔 =
𝑹 𝒂+𝑳 𝒂 𝒔
𝑲 𝒕
𝑻 𝒎(𝒔) + 𝑲 𝒃 𝒔𝜽 𝒎 𝒔

53. Mechanical Loading of the Rotor
• We must find
𝑇 𝑚 𝑠
𝜃 𝑚 𝑠
if we want to obtain the transfer function
𝜃 𝑚 𝑠
𝐸 𝑎 𝑠
• Jm is the equivalent inertia at the armature and includes both the
armature inertia, and (as we will see later) the load inertia
reflected to the armature.
𝑇 𝑚 𝑠 = 𝐽 𝑚 𝑠2 + 𝐷 𝑚 𝑠 𝜃 𝑚 𝑠
• Back-substituting in previous equation
𝐸 𝑎 𝑠 =
𝑹 𝒂+𝑳 𝒂 𝒔
𝑲 𝒕
𝐽 𝑚 𝑠2 + 𝐷 𝑚 𝑠 𝜃 𝑚 𝑠 + 𝐾𝑏 𝑠𝜃 𝑚 𝑠
• Assuming that 𝐿 𝑎 ≪ 𝑅 𝑎
The motor transfer
function can simply be
written as
𝜽 𝒎 𝒔
𝑬 𝒂 𝒔
=
𝑲
𝒔 + 𝜶

54. Assignment 2d
• What happens when the motor is connected to
a load through a gear? Write the transfer
function.