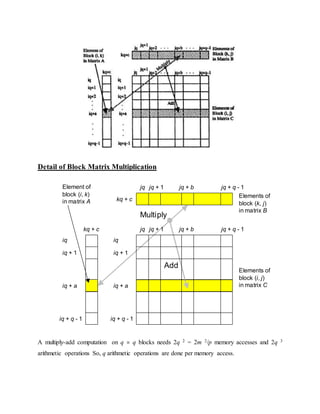
The document discusses parallel processing and matrix multiplication. It introduces parallel processing concepts like dividing a task between multiple processors to complete it faster. As an example, it explains how two people can add 100 numbers in half the time it takes one person. It then discusses using parallel processing to compute the convex hull of a set of points by dividing the set in half and merging the results. The rest of the document focuses on computational models for parallel processing like PRAM and different types of PRAM models including EREW, CREW, CRCW and how they handle read/write conflicts. It also provides an example of using parallel processing to perform matrix multiplication faster by dividing the matrices and merging the results.

1. Report on
Matrix Multiplication using Parallel Processing
Subject
Advance Computer Architecture
Submitted To
Mr. Asim Munir
Class
MSCS-F14
Prepared by: Sunawar Khan
Reg No: 813-MSCS-F14

2. Matrix Multiplication using Parallel Processing
Parallel Processing
Introduction to parallel processing
There are many application in day to day life that demand real time solution to problem. For
example weather forecasting has to done in a timely fashion etc.. If an expert system is used to
aid a physician in surgical procedures ,decisions have to be made within seconds. And so on.
Programs written for such applications have to perform an enormous amount of computation.
Even the fastest single-processor machine may not be able to come up with solutions within
tolerable time limits. Parallel Random Access Machines (PRAM) offer the potential of
decreasing the solution times enormously. E.g.
Say there are 100 numbers to be added and there are two persons A and B. Person A can add the
first 50 numbers. At the same time B can add the next 50 numbers. When they are done, one of
them can add two individual sums to get the final answer. So two people can add the 100
numbers in almost half the time required by one.
Here is another example of Computing Convex Hull using parallel processing

3. Take the set of points and divide the set into two halves Assume that recursive call computes the
convex hull of the two halves Conquer stage: take the two convex hulls and merge it to obtain
the convex hull for the entire set.
What is Computational Model
“A computational model is a mathematical model in computational science that requires
extensive computational resources to study the behavior of a complex system by computer
simulation.”
Random access machine model
Algorithms can be measured in a machine-independent way using the Random Access Machine
(RAM) model. This model assumes a single processor. In the RAM model, instructions are
executed one after the other, with no concurrent operations. This model of computation is an
abstraction that allows us to compare algorithms on the basis of performance. The assumptions
made in the RAM model to accomplish this are:
 Each simple operation takes 1 time step.
 Loops and subroutines are not simple operations.
 Each memory access takes one time step, and there is no shortage of memory.
For any given problem the running time of algorithms is assumed to be the number of time steps.
The space used by an algorithm is assumed to be the number of RAM memory cells.
A model of computation whose memory consists of an unbounded sequence of registers, each of
which may hold an integer. In this model, arithmetic operations are allowed to compute the
address of a memory register.
In the RAM (Random Access Machine) we assume that any of the following operation can be
done in one unit of time: addition, subtraction, multiplication, division, comparison, memory
access, assignment, and so on. This model widely accepted as a valid sequential model.
An important feature of parallel computing that is absent in sequential computing is need for
interprocessor communication. For example given any problem, the processor have to
communicate among themselves and agree on the subproblems each will work on. Also they
need to communicate to see whether everyone has finished its task so on.

4. PRAM Modelfor Single ProcessorMachine.
The designer of sequential algorithm typically formulates the algorithm using an abstract model
of computation called random access machine(RAM). In this model, the machine consist of a
single processor connected to a memory system. Each CPU include arithmetic operation, logical
operation, and memory access require one step access.
 Standard Random Access Machine
 Each Operation load, store, jump, add, etc takes one unit of time.
 Simply general one model.
 Basic model for sequential algorithm
 Unbounded number of local memory cells
 Each memory cell can hold an integer of unbounded size
 Instruction set included –simple operations, data operations, comparator, branches
 All operations take unit time
 Time complexity = number of instructions executed
 Space complexity = number of memory cells used
Parallel Machine or multiprocessor Model
We begin this discussion with an ideal parallel machine called Parallel Random Access Machine,
or PRAM. A multiprocessor model is a generalization of the sequenatial RAM Model in which
there is more than one processor. Multiprocessor model can be classified into three basic types,
local memory machine, modular memory machine, and Parallel Random-Access Machien. Each
describe figure below

5. “The Parallel Random Access Machine (PRAM) is an abstract model for parallel computation
which assumes that all the processors operate synchronously under a single clock and are able to
randomly access a large shared memory.”
 A natural extension of the Random Access Machine(RAM), serial architecture is the
Parallel Random Access Machine, or PRAM
 Pram Consist of p Processor and a global memory of unbounded size that is uniformly
accessible to all processors
 Processors share a common clock but may execute different instruction in each cycle
PRAM Architecture
The parallel version of RAM constitutes an abstract model of the class of global-memory parallel
processors. The
abstraction consists of ignoring the details of the processor-to-memory interconnection network

6. and taking the view that each processor can access any memory location in each machine cycle,
independent of what other processors are doing.
Processor i can do the following in three phases of one cycle:
 Fetch a value from address si in shared memory
 Perform computations on data held in local registers
 3. Store a value into address di in shared memory
Is an abstract machine for designing the algorithms applicable to parallel computers
 Unbounded collection of RAM processors P0, P1, …,
 Processors don’t have tape
 Each processor has unbounded registers
 Unbounded collection of share memory cells
 All processors can access all memory cells in unit time
 All communication via shared memory

7.  Two or more processors may read simultaneously from the same cell
 A write conflict occurs when two or more processors try to write simultaneously into
the same cell
Classification of PRAM Model
The classification in is reminiscent of Flynn’s classification and offers yet another example of
the quest to invent four-letter abbreviations/acronyms in computer architecture! Note that here,
too, one of the categories is not very useful, because if concurrent writes are allowed, there is no
logical reason for excluding the less problematic concurrent reads. EREW PRAM is the most
realistic of the four submodels (to the extent that thousands of processors concurrently accessing
thousands of memory locations within a shared memory address space of millions or even
billions of locations can be considered realistic!). CRCW PRAM is the least restrictive
submodel, but has the disadvantage of requiring a conflict resolution mechanism to define the
effect of concurrent writes (more on this below). The default submodel, which is assumed when
nothing is said about the submodel, is CREW PRAM. For most computations, it is fairly easy to
organize the algorithm steps so that concurrent writes to the same location are never attempted.
CRCW PRAM is further classified according to how concurrent writes are handled. Here are a
few example submodels based on the semantics of concurrent writes in CRCW PRAM:
EREW
Least “powerful”,
most “realistic”
CREW
Default
ERCW
Not useful
CRCW
Most “powerful”,
further subdivided
Reads from same location
Writestosamelocation
Exclusive
Concurrent
Concurrent
Exclusive

8. CRCW SubModel
• Undefined: In case of multiple writes, the value written is undefined (CRCW-U).
• Detecting: A special code representing “detected collision” is written (CRCW-D).
Common: Multiple writes allowed only if all store the same value (CRCW-C). This is
sometimes called the consistent-write submodel.
• Random: The value written is randomly chosen from among those offered (CRCWR).
This is sometimes called the arbitrary-write submodel.
• Priority: The processor with the lowest index succeeds in writing its value (CRCW-P).
• Max/Min: The largest/smallest of the multiple values is written (CRCW-M).
• Reduction: The arithmetic sum (CRCW-S), logical AND (CRCW-A), logical XOR
(CRCW-X), or some other combination of the multiple values is written.
Physical Complexity
 Processors and memories are connected via switches.
 Since these switches must operate in O(1) time at the level of words, for a system of p
Processors and m words, the switch is O(mp).
 Clearly, for meaningful values of p and m, a true PRAM is not realizable

9. Relationship between different PRAM Submodel
The following relationships have been established between some of the PRAM submodels:
EREW < CREW < CRCW-D < CRCW-C < CRCW-R < CRCW-P
Even though all CRCW submodels are strictly more powerful than the EREW submodel, the
latter can simulate the most powerful CRCW submodel listed above with at most logarithmic
slowdown.
A p-processor CRCW-P (priority) PRAM can be simulated by a p-processor EREW PRAM with
a slowdown factor of Θ(log p). EREW PRAM to sort or find the smallest of p values in Θ(log p)
time, as we shall see later. To avoid concurrent writes, each processor writes an ID-address-value
triple into its corresponding element of a scratch list of size p, with the p processors then
cooperating to sort the list by the destination addresses, partition the list into segments
corresponding to common addresses (which are now adjacent in the sorted list), do a reduction
operation within each segment to remove all writes to the same location except the one with the
smallest processor ID, and finally write the surviving address-value pairs into memory. This final
write operation will clearly be of the exclusive variety.
Matrix Multiplication
Introduction to Matrix Multiplication.
We will show how to implement matrix multiplication C=C+A*B on several of the
communication networks discussed in the last lecture, and develop performance models to
predict how long they take. We will see that the performance depends on several factors.
we discuss PRAM matrix multiplication algorithms as representative examples of the class of
numerical problems. Matrix multiplication is quite important in its own right and is also used as
a building block in many other parallel algorithms. For example, matrix multiplication is useful
in solving graph problems when the graphs are represented by their adjacency or weight
matrices. Given m × m matrices A and B, with elements a i jand b ij,, their product C is defined
as

10. The following O(m³)-step sequential algorithm can be used for multiplying m × m matrices:
Sequential matrix multiplication
for i = 0 to m – 1 do
for j = 0 to m – 1 do
t := 0
for k = 0 to m – 1 do
t := t + aikbkj
endfor
cij := t
endfor
endfor
Consider n*n matric multiplication with n3 processors
 Each cij=∑ k=1..n aik bkj be computed on the CREW PRAM in parallel using n processors n
O(log n) time.

11.  On the EREW PRAM exclusive read of aij and bij values can be satisfied by making n
copies of a and b, which takes O(log n) time with n Processors
 Total time is still O(log n)
 Memory requirement is ofcourse much higher for the EREW PRAM
 Complexity: Θ(n3)
 Better Algorithm that improve slightly
 Multiplication by block
PRAM matrix multiplication using m2 processors
Proc (i, j), 0  i, j < m, do
begin
t := 0
for k = 0 to m – 1 do
t := t + aikbkj
endfor
cij := t
end
Because multiple processors will be reading the same row of A or the same column of B, the
above naive implementation of the algorithm would require the CREW submodel. However, it is
possible to convert the algorithm to an EREW PRAM algorithm by skewing the memory
accesses (how?).
matrix multiplication can be done in Θ(m²) time by using Processor i to compute the m elements
in Row i of the product matrix C in turn.
PRAM Matrix Multiplication with m Processors
for j = 0 to m – 1 Proc i, 0  i < m, do
t := 0
for k = 0 to m – 1 do
t := t + aikbkj

12. endfor
cij := t
endfor
m processors read A at once (no concurrent)
- All m processors read same column of B at same time (concurrent read should be allowed)
- if not then, Brent’s theorem states – we can convert CREW -> EREW by skewing memory
access
More Efficient Matrix Multiplication (for NUMA)
On the Cm* NUMA-type shared-memory multiprocessor, a research prototype machine built at
Carnegie-Mellon University in the 1980s, this block matrix multiplication algorithm exhibited
good, but sublinear, speed-up. With 16 processors, the speed-up was only 5 in multiplying 24 ×
24 matrices. However, the speed-up improved to about 9 when larger 36 × 36 (48 × 48) matrices
were multiplied. It is interesting to note that improved locality of the block matrix multiplication
algorithm can also improve the running time on a uniprocessor, or distributed shared-memory
multiprocessor with caches, in view of higher cache hit rates.

13. Detail of Block Matrix Multiplication
A multiply-add computation on q  q blocks needs 2q 2 = 2m 2/p memory accesses and 2q 3
arithmetic operations So, q arithmetic operations are done per memory access.
iq + q - 1
iq + a
iq + 1
iq
jq jq + b jq + q - 1
kq + c
kq + c
iq + q - 1
iq + a
iq + 1
iq
jq jq + 1 jq + b jq + q - 1
Multiply
Add
Elements of
block (i, j)
in matrix C
Elements of
block (k, j)
in matrix B
Element of
block (i, k)
in matrix A
jq + 1

14. A Simple Parallel Algorithm
Example for n numbers addition:
1. We start with 4 processors and each of them adds 2 items in the first step.
2. The number of items is halved at every subsequent step. Hence logn steps are required
for adding n numbers.
3. The processor requirement is O(n).
CREW Cost
Let P(n) = O(n2)
 Read n2 processors Aij all cells at once in = O(1)
 Read n2 processors Bij all cells in = O(1)
 Each processor multiply Aij* Bij in = O(1)
 Parallel Sum to get Cij = O(logn)
 Store Value Cij = O(1)
 T(n) = O(log n)
 P(n) = O(n2)
 W(n) = O(n2log n) = total # of all operations
EREW Cost
Let P(n) = O(n2)
 Read n2 processors Aij all cells at once in = O(1)
 Cannot read n2 processors Bij all cells in = O(1)
 Concurrent read is not allowed
 Skew the memory – replicate – or - Parallel processor read
 O(logn)
 Each processor multiply Aij* Bij in = O(1)
 Parallel Sum to get Cij = O(logn)
 Store Value Cij = O(1)
 T(n) = O(log n)
 P(n) = O(n2)
 W(n) = O(n2log n) = total # of all operations

15. Advantages of PRAM Model
 PRAM removes algorithmic details concerning synchronization and communicating,
allowing the algorithm designer to focus on problem properties
 A PRAM algorithm includes an explicit understanding of the operation performed at each
time unit and an explicit allocation of processors to jobs at each time unit.
 PRAM designer paradigm have turned out to be robust and have been mapped efficiently
onto many other parallel models and even network models
Disadvantage of PRAM Model
 Model Inaccuracies
unbounded local memory(register)
All operation takes unit time
processors run in lock steps
 Unaccounted costs
Non-local memory access
Latency
Bandwidth
Memory Access Contention
Conclusion
 PRAM algorithm is the source of most fundamental ideas
 It’s a source of inspiration for algorithms
 PRAM is simple and easy to understand.
The improved locality of block matrix multiplication can also improve the running time on a
uniprocessor, or distributed shared-memory multiprocessor with caches.
Reason: Higher Cache Higher Hit Rates