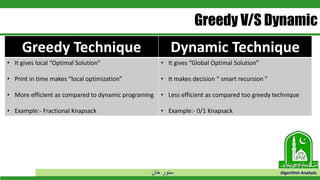
This document discusses greedy algorithms and dynamic programming. It explains that greedy algorithms find local optimal solutions at each step, while dynamic programming finds global optimal solutions by considering all possibilities. The document also provides examples of problems solved using each approach, such as Prim's algorithm and Dijkstra's algorithm for greedy, and knapsack problems for dynamic programming. It then discusses the matrix chain multiplication problem in detail to illustrate how a dynamic programming solution works by breaking the problem into overlapping subproblems.

1. Sunawar Khan
Islamia University of Bahawalpur
Bahawalnagar Campus
Analysis o f Algorithm

2. ‫خان‬ ‫سنور‬ Algorithm Analysis
Counting Sort
Linear Time Sorting
Bucket Sort
Radix Sort
Contents

3. ‫خان‬ ‫سنور‬ Algorithm Analysis
Greedy Method v/s Dynamic Programing
• Both are used for Optimization problem. It required minimum or
maximum results.
• In Greedy Method:- Always follow a function until you find the optimal
result whether it is maximum or minimum.
• Prims algorithm for MST
• Dijkstra Algorithm for finding shortest path.

4. ‫خان‬ ‫سنور‬ Algorithm Analysis
Greedy Method v/s Dynamic Programing
• In Dynamic programing we will try to find all possible solution and
then we’ll pick the best solution which is optimal.
• It is time consuming as compared to greedy method.
• It use recursive formulas for solving problem.
• It follows the principal of optimality.

5. ‫خان‬ ‫سنور‬ Algorithm Analysis
Greedy V/S Dynamic
Greedy Technique Dynamic Technique
• It gives local “Optimal Solution”
• Print in time makes “local optimization”
• More efficient as compared to dynamic programing
• Example:- Fractional Knapsack
• It gives “Global Optimal Solution”
• It makes decision “ smart recursion ”
• Less efficient as compared too greedy technique
• Example:- 0/1 Knapsack

6. ‫خان‬ ‫سنور‬ Algorithm Analysis
Principle of Optimality
• Principle of optimality says that a problem can be solved by sequence
of decisions to get the optimal solution.
• It follows Memoization Problem

7. ‫خان‬ ‫سنور‬ Algorithm Analysis
Fibonacci Series
൞
0 𝑖𝑓 𝑛 = 0
1 𝑖𝑓 𝑛 = 1
𝑓𝑖𝑏 𝑛 − 2 + 𝑓𝑖𝑏 𝑛 − 1 𝑖𝑓 𝑛 > 1
𝑖𝑛𝑡 𝑓𝑖𝑏(𝑖𝑛𝑡 𝑛){
if(n <= 1)
return 1
return fib(n-2)+fib(n-1);
}

8. ‫خان‬ ‫سنور‬ Algorithm Analysis
Running Example
• If we wanna find out the fib(5)
fib (5)
fib(3)
fib(1) fib(2)
fib(0) fib(1)
fib(4)
fib(2)
fib(0) fib(1)
fib(3)
fib(1) fib(2)
fib(0) fib(1)

9. ‫خان‬ ‫سنور‬ Algorithm Analysis
What?
• It is a strategy in designing of algorithm which is used when problem
breaks down into recurring small problems.
• It is typically applicable to optimization problems
• In such problems there can be many solution, each solution has a
value and we wish to find a solution with the optimal value.

10. ‫خان‬ ‫سنور‬ Algorithm Analysis
Elements of Dynamic Programming
• Simple Subproblems
• We should be able to break the original problem to small subproblems that
have the same structure
• Optimal substructure of problem
• The optimal solution to the problem contains within solution to its
subproblems.
• Overlapping Subproblems
• There exist some places where we solve the same subproblem more than once

11. ‫خان‬ ‫سنور‬ Algorithm Analysis
Steps to design Dynamic Programming Algo
• Characterize optimal substructure
• Recursively define the value of an optimal solution
• Compute the vale bottomUp
• (if needed) constraints an optimal solution

12. ‫خان‬ ‫سنور‬ Algorithm Analysis
Applications
• Matrix Chain Multiplication
• Optimal Binary Search Tree
• All Pairs Shortest Path Problems
• Travelling Salesperson Problem
• 0/1 Knapsack Problem
• Reliability Design

13. ‫خان‬ ‫سنور‬ Algorithm Analysis
Matrix Chain Multiplication
13x15 05x89 89x03 03x34
1 2 3 4
1 0
2 0
3 0
4 0
m[1,1] m[2, 2] m[3, 3] m[4, 4]
m
A CB D

14. ‫خان‬ ‫سنور‬ Algorithm Analysis
Matrix Chain Multiplication
1 2 3 4
1 0 5785
2 0 1335
3 0 9078
4 0
m[1, 2] m[2, 3] m[3, 4]
m
m[A, B] m[B, C] m[C, D]
m
A CB D
13x05 05x89 89x03 03x34
13x05 05x89 05x89 89x03 89x03 03x34
13x05x89 05x89x3 89x3x4
5785 1335 9078

15. ‫خان‬ ‫سنور‬ Algorithm Analysis
Matrix Chain Multiplication
1 2 3 4
1 0 5785 1530
2 0 1335
3 0 9078
4 0
m[1, 3]
m
A.(B.C) (A.B).C
m
A CB D
13x05 05x89 89x03 03x34
2 Possibilities
13x05 05x89 89x03
1530
m[1, 1] m[2,3] 13 x 5 x 3
Cost A Cost B.C Cost A.B.C = 13x5x3
0 + 1335 + 195
13x05 05x89 89x03
9256
m[1, 2] m[3,3] 13 x 89x 3
5785 + 0 + 3471

16. ‫خان‬ ‫سنور‬ Algorithm Analysis
Matrix Chain Multiplication
1 2 3 4
1 0 5785 1530
2 0 1335 1845
3 0 9078
4 0
m[1, 3]
m
B.(C.D) (B.C).D
m
A CB D
13x05 05x89 89x03 03x34
2 Possibilities
05x89 89x03 03x34
24208
m[2, 2] m[3, 4] 05 x 89 x 34
Cost B Cost C.D Cost B.C.D = 05x89x34
0 + 9078 + 15130
05x89 89x03 03x34
1845
m[2, 3] m[4, 4] 5 x 3 x 34
1330 + 0 + 510

17. ‫خان‬ ‫سنور‬ Algorithm Analysis
Matrix Chain Multiplication
•m[1, 4]
m[1, 4] = min{m[1,1] + m[2,4], 13 x 5 x 34,
m[1, 2] + m[3, 4] + 13 x 89 x 34,
m[1, 3] + m[4, 4] + 13 x 3 x 34 }

18. ‫خان‬ ‫سنور‬ Algorithm Analysis
Matrix Chain Multiplication
•m[1, 4]
m[1, 4] = min{A. (B. C. D), (A.B).(C.D),(A.B.C).D}

19. ‫خان‬ ‫سنور‬ Algorithm Analysis
Matrix Chain Multiplication
•m[1, 4]
m[1, 4] = min{0 + 1845 + 2210,
5789 + 78 + 39338,
1530 + 0 + 1326}

20. ‫خان‬ ‫سنور‬ Algorithm Analysis
Matrix Chain Multiplication
•m[1, 4]
m[1, 4] = min{4055, 54201, 2856}
WHAT IS MIN? 2856
1 2 3 4
1 0 5785 1530 2856
2 0 1335 1845
3 0 9078
4 0
mm

21. ‫خان‬ ‫سنور‬ Algorithm Analysis
Formula
•m[i, j] = min{m(I, k) + m(k+1, j) + di-1xdkxdj}